Минимизация функции нескольких переменных без ограничений
2.1. Постановка задачи
Сформулируем
постановку задачи: минимизировать
функцию
при отсутствии ограничений. Для задачи
нелинейного программирования при
отсутствии ограничений необходимыми
условиями того, что
- точка локального минимума, являются:
функцию
дифференцируема в точке
,
)
= 0, т.е. существует стационарная точка
в
.
Достаточные условия того, что - точка локального минимума, кроме
приведенных условий 1) и 2) включает следующее:
3)
)
0, т.е. матрица Гессе положительно
определенная.
Если
- выпуклая функция при всех
,
,
то необходимым и
достаточным условием минимума является условие: ) = 0.
Процедура аналитического решения.
Проверяем выпуклость.
Если да, то решаем относительно
,…,
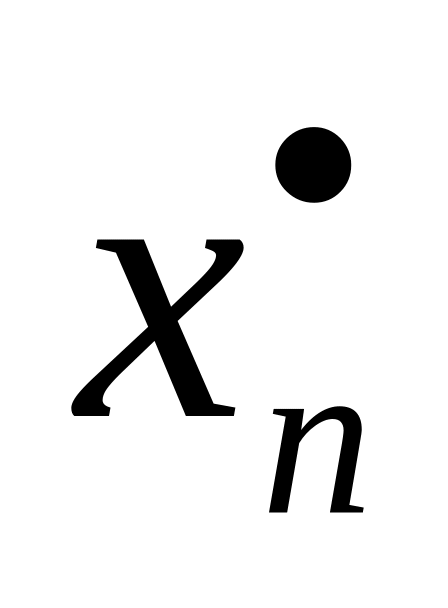систему уравнений
) = 0.
Если нет, то находим все множество
,…,
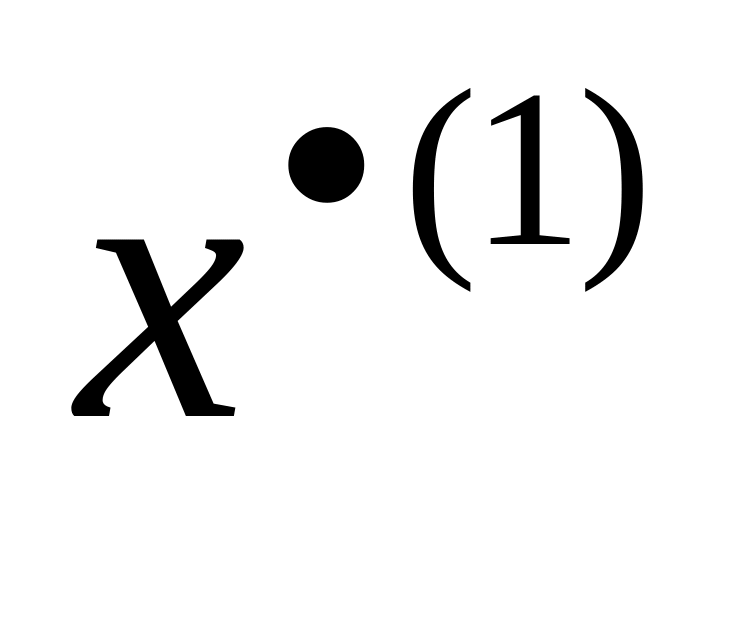решений уравнений
)
= 0.Отбираем подмножество решений
,
где
)
является выпуклой функцией. Если нет
таких точек, значит решения нет.
Если есть, то из отобранных решений выбираем точку с наименьшим значением ).
В качестве примера
рассмотрим случай целевой функции от
двух переменных
.
Если она в точке
имеет экстремум, то в этой точке либо
ее частные производные первого порядка
равны нулю, либо хотя бы одна из них не
существует. Точка
называется критической (стационарной)
точкой.
2.2. Детализация достаточных условий экстремума.
Сначала рассмотрим достаточные условия экстремума для функции двух переменных. Пусть в окрестности критической точки функция имеет непрерывные частные производные до второго порядка включительно. Рассмотрим определитель матрицы Гессе
=
-
(
)
и
Если
и
,
то в точке
имеет минимум. Если
и
,
то в точке
имеет максимум.
Достаточные условия
экстремума для функции
переменных. Если
определитель матрицы
Гессе и все
главные миноры больше 0, то эта стационарная
точка является минимумом
.
Если ее определитель и все главные
миноры меньше 0, то эта стационарная
точка является максимумом
.
Если ее определитель и главные миноры
имеют разные знаки, то вышеуказанная
стационарная точка не является экстремумом
функции
.
Главным минором
- го порядка матрицы называется минор,
образованный её первыми
строками и
столбцами.
Рассмотрим последовательно случаи, когда возможно получение аналитического решения оптимальных задач без ограничений.
Лекция 9. 2.3. Сепарабельные функции
Определение.
Функция
называется сепарабельной, если она
представляется в следующем виде:
=
+
,
где
- некоторая константа.
Функции
называются частными функциями.
Глобальный минимум
сепарабельной
функции
достигается в точке минимума каждой из
функций
,
в силу независимости точки глобального
минимума каждой из функций
,
от точек глобального минимума остальных
функций. Глобальный максимум сепарабельной
функции
достигается в точке глобального максимума
каждой из функций
,
в силу независимости точки глобального
максимума каждой из функций
,
от точек глобального максимума остальных
функций. Необходимыми и достаточными
условиями того, что
- точка
локального минимума
,
являются:
1) , дифференцируема в точке ,
2)
,
т.е.
является стационарной точкой,
3)
.
Точка глобального минимума , определяется перебором точек её локального минимума.
Необходимыми и достаточными условиями того, что - точка локального максимума , являются:
1) , дифференцируема в точке ,
2) , т.е. является стационарной точкой,
3)
.
Точка глобального максимума , определяется перебором точек её локального максимума.