Библиографические ссылки

1. Выготский Л.С. Педагогическая психология. М.: Педагогика, 1991.

2. Дистервег А. Руководство к образованию немецких учителей. Избранные педагогические сочинения. М.: Учпедгиз, 1956.

3. Концепция духовно-нравственного развития и воспитания личности гражданина России [А.Я. Данилюк, А.М. Кондаков, В.А. Тишков]. 2-е изд. М.: Просвещение, 2010.

4. Гинецинский В.И. Основы теоретической педагогики. СПбГУ, 1992.

5. Никитина Н.Н. Введение в педагогическую деятельность: Теория и практика: учеб. пособие для студ. высш. пед. учеб. заведений. М.: ИЦ «Академия», 2004.

6. Федеральный государственный образовательный стандарт начального общего образования / М-во образования и науки Рос. Федерации. М.: Просвещение, 2010.

С. В. Маслова, л. А. Янкина

Мордовский государственный педагогический институт

им. М.Е. Евсевьева,

г. Саранск

maslovasv@mail.ru

Возможности организации самостоятельной работы студентов в рамках фгос впо

___________________________________________

В статье рассматриваются формы организации самостоятельной работы студентов на лекциях, практических занятиях, при проведении исследовательской работы. Особое внимание уделяется заданиям интегрированного характера, направленным на методико-математическую подготовку будущих учителей начальных классов.

Ключевые слова: самостоятельная работа, компетенции, интегрированные задания, дисциплины математической направленности.

В Федеральном государственном образовательном стандарте высшего профессионального образования по направлению подготовки 050100 – Педагогическое образование выделены следующие компетенции, которыми должен обладать выпускник: способность понимания сущности и значения информации в развитии современного информационного общества; способность использования систематизированных теоретических и практических знаний гуманитарных, социальных и экономических наук при решении социальных и профессиональных задач; способность использования возможности образовательной среды для формирования универсальных видов учебной деятельности и обеспечения качества учебно-воспитательного процесса; способность разработки современных педагогических технологий с учетом особенностей образовательного процесса, задач воспитания и развития личности [1].

В решении задачи по формированию и развитию этих и других компетенций важное место отводится самостоятельной работе студентов (СРС), которая является одной из важнейших составляющих учебного процесса. В ходе СРС происходит не только формирование знаний, умений и навыков, но и обеспечивается усвоение студентом приемов познавательной деятельности. Самостоятельная работа организуется и реализуется в учебно-воспитательном процессе в качестве целостной системы, пронизывающей все этапы обучения студентов в вузе.

Повышение роли СРС не всегда означает переход к каким-либо кардинально новым видам учебной работы. Дело в методиках проведения традиционно используемых форм обучения (лекций, практических занятий, исследовательских работ и др.). Рассмотрим формы организации самостоятельной работы студентов – будущих учителей начальных классов при изучении дисциплин математической направленности.

Лекция является основной формой вузовского обучения. Одна из задач лекционных курсов математики и методики ее преподавания на педагогическом факультете – формирование у студентов системы знаний, включающей как общие понятия математики (множество, отношения, математические утверждения и др.), так и вопросы, связанные с понятиями начального курса математики (натуральное число, операции над числами, свойства этих операций; величины и их свойства и др.), сведения из истории математики. Знания, которые сообщаются студенту на лекции, – это знания преподавателя. Для того чтобы они стали знаниями студента, необходимо, чтобы студент приложил определенные усилия для их получения, проявил самостоятельность мышления. Лектор должен использовать возможности читаемого курса для привлечения студентов к самостоятельному «открытию» тех или иных научных фактов, к получению математических терминов, формулировок определений и теорем, доказательств.

Так, например, при изучении отношений между множествами после определения пересекающихся множеств студенты могут самостоятельно, по аналогии, получить термин и сформулировать определение непересекающихся множеств, сделать соответствующую иллюстрацию. При рассмотрении методики изучения арифметических действий студент опирается на знания, полученные в курсе математики, демонстрируя всевозможные иллюстрации, которые могут быть использованы при объяснении данного материала в начальной школе.

Для самостоятельной работы студентам можно оставить доказательство теоремы, которое проводится аналогично рассмотренному на лекции (самостоятельно разобрать доказательство студенты могут здесь же на лекции или дома). Без помощи преподавателя студенты также могут составлять различные схематические рисунки к составным текстовым задачам, опираясь на рассмотренные аналогичные чертежи, представленные к простым задачам.

Кроме того, с целью активизации самостоятельной деятельности студентов на лекции целесообразно использование проблемных ситуаций. Например, возможно демонстрировать те проблемные ситуации, которые учитель создает при рассмотрении той или иной темы с младшими школьниками, предлагая будущим учителям, во-первых, разрешить ее, а во-вторых, создать подобные, не упуская из виду основную цель данного урока. Также могут быть использованы выступления студентов с небольшими сообщениями по некоторым вопросам курса (например, с исторической справкой или методическими замечаниями).

На практических занятиях преподаватель обычно старается прорешать со студентами максимальное количество самых разнообразных задач. При этом необходимо учитывать особенности задачного материала. Если задача алгоритмическая, то отработку навыка решения подобных задач можно предоставить студентам для самостоятельной работы, рассмотрев на занятии алгоритм решения задачи. При этом алгоритм не обязательно предъявлять студентам в готовом виде. Он может быть получен студентами самостоятельно или при частичной помощи преподавателя. Задачи неалгоритмического характера (исследовательские, творческие) рассматриваются, как правило, на занятии. Студенту предоставляется возможность найти решение самостоятельно, при необходимости оказывается дозированная помощь (помощь может оказать не только преподаватель, но и успевающий студент). Задачи могут носить как математический, так и методический характер. Например, при работе с конспектами уроков студенты могут самостоятельно менять местами предлагаемые задания, изменять их формулировки на более продуктивные (аргументировав изменение), придумывать свои задания, которые, на их взгляд, в большей степени отвечают поставленной учебной задаче.

В соответствии с ФГОС ВПО на внеаудиторную работу студентов отводится не менее половины бюджета времени. В связи с этим преподавателю необходимо тщательно продумать, какие вопросы изучаемого курса можно предложить студентам для самостоятельного изучения. Это должен быть доступный для самостоятельной работы материал. Кроме того, студенты должны быть обеспечены литературой и иметь навыки (или получить рекомендации) самостоятельной работы с ней. СРС может быть обращена как к работе с литературными источниками, так и к работе с Интернет-ресурсами. Например, сеть Интернет содержит богатый материал по истории математики, обширную базу конспектов уроков в начальной школе, тестовые задания для младших школьников по математике.

Работа студентов по самостоятельному изучению некоторого материала пройдет более успешно при четком руководстве преподавателя. Студентам можно предложить план изучаемой темы, где выделены основные понятия и теоремы, а также вопросы к данной теме, с помощью которых можно осуществлять контроль за усвоением. Изучение нового материала осуществляется на базе знаний, полученных студентами ранее (в школе или при изучении предыдущих тем). Однако изучение новой темы не будет успешным, если необходимые базовые знания окажутся с пробелами и потребуется тратить драгоценное аудиторное время на восполнение имеющихся пробелов. Поэтому преподавателю необходимо по каждой теме курса выявить систему базовых знаний и умений. Повторение пройденного материала, необходимого для изучения нового, можно предоставить студентам для домашней самостоятельной работы.

Одной из форм организации СРС при изучении методико-математических дисциплин являются так называемые индивидуальные задания. Каждый студент получает набор заданий по изучаемой в данном семестре теме (темам). Работа над заданиями ведется непрерывно в течение семестра по мере изучения тех или иных вопросов. Контроль за выполнением индивидуальных заданий проводится в виде собеседования, где студент обязан ответить на любой вопрос преподавателя, связанный с решением той или иной задачи. Студент в течение семестра сдает задачи, усваивая постепенно необходимые знания. Равномерное распределение учебной нагрузки и контроля способствует снижению напряжения перед экзаменом (ведь основной материал уже усвоен). К недостатку этой формы деятельности следует отнести то, что контроль за выполнением индивидуальных заданий происходит за счет личного времени преподавателя. В основном задания, предлагаемые преподавателями для самостоятель­ной работы студентов, имеют узконаправленный предметный характер. Но с позиций компетентностного подхода к обучению целесообразно использовать в практике интегрированные задания. Рассмотрим некоторые примеры подобных задач и попробуем восстановить рассуждения студентов в процессе их выпол­нения.

«Укажите различные подходы к понятию натурального числа, которые могут быть использованы при решении задач. Обоснуйте выбор действия в каждом из подходов. Использование какого из трех подходов к понятию нату­рального числа наиболее целесообразно в каждом из случаев?

а) В одной коробке 6 карандашей. Сколько карандашей в трех таких ко­робках? б) На нашей улице строят девятиэтажный дом. 5 этажей уже по­строили. Сколько этажей еще нужно построить?».

При решении текстовых задач могут быть использованы три подхода к формированию понятия числа: теоретико-множественный, аксиоматический и число как мера величины.

Выбор арифметического действия в первом случае связан с определе­ниями этих действий в данной теории: мы находим количество элементов либо в объединении множеств (сложение и умножение), либо в дополнении одного множества до другого (вычитание), либо в равномощных подмножествах или количество самих подмножеств (деление).

Во втором случае выбор арифме­тического действия опирается на понятие множества натуральных чисел в аксиоматической теории как множества, для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее четырем аксиомам Дж. Пеано.

Выбирая арифметическое действие с опорой на третий подход к понятию натурального числа, помним, что натуральное число как мера отрезка а показы­вает, из скольких выбранных единичных отрезков е состоит отрезок а.

Обращаясь к предложенным задачам начального курса математики, от­метим, что первую из них целесообразно решать, опираясь на теоретико-мно­жественный подход к понятию числа.

В теории множеств одно из определений умножения звучит следующим образом: «Произведением целых неотрицательных чисел а и b называется це­лое неотрицательное число аb, удовлетворяющее условиям:

1)  при b > 1; 2) а ∙ 1 = а при b = 1; 3) а ∙ 0 = 0 при b = 0»

По условию задачи а = 6, b = 3. Так как b>1, то 6∙3 = 6 + 6 + 6 = 18 (карандашей). Решение данной задачи может сопровождаться рисунком (рис. 1).

Рис. 1.

Решение второй из предложенных задач целесообразно строить, обраща­ясь к понятию числа как мере величины.

В качестве единицы измерения выбираем один этаж, относительно чего и строим соответствующий чертеж (рис. 2).

Рис. 2.

Задача решается с опорой на предложенный рисунок.

 «Составьте задания, иллюстрирующие сравнение дробей: а) с одинако­выми числителями; б) с одинаковыми знаменателями»

Пару чисел, записанную в виде , где m, n ∈ N, называют обыкновенной дробью. У дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше, и меньше та, знаменатель которой больше. Можно предложить такое задание: «Опираясь на рисунок, запиши дроби и сравни их» (рис. 3).

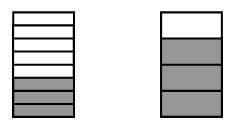
Рис. 3.

У дробей с одинаковыми знаменателями больше та дробь, числитель которой больше, и меньше та, числитель которой меньше. Можно предложить аналогичное задание: «Опираясь на рисунок, запиши дроби и сравни их» (рис. 4), несколько видоизменив рисунок.

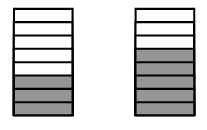
Рис. 4.

 «Какие математические законы лежат в основе умножения числа на произведение, деления суммы на число?»

Рассматривая в начальном курсе математики правило умножения числа на произведение, учащиеся заучивают следующее правило: «Умножить число на произведение можно тремя способами: 1) вычислить произведение в скобках, а затем число умножить на полученный результат; 2) число умножить сначала на первый множитель, а затем полученный результат умножить на второй; 3) число умножить на второй множитель, а затем полученный результат умножить на первый».

Данное правило используется, например, при выполнении следующего задания: «Можно ли утверждать, что значения выражений в каждом столбце одинаковые?

8 · (4 · 6) (9 · 3) · 2

8 · 24 2 · 27

(8 · 4) · 6 9 · (3 · 2)

32 · 8 (3 · 2) · 8

6 · 32 (2 · 3) · 9».

В основе этого правила лежит ассоциативный закон умножения: «Для любых натуральных чисел а, b и с справедливо следующее утверждение: с · (а · b) = (с · а) · b».

Рассматривая в начальном курсе математики правило деления суммы на число, учащиеся также заучивают правило: «Разделить сумму на число можно двумя способами: 1) вычислить сумму в скобках, а затем полученный результат разделить на число; 2) разделить каждое слагаемое на число, а полученные результаты сложить».

Данное правило используется при выполнении следующего задания: «Чем похожи выражения в каждой паре? Чем отличаются?

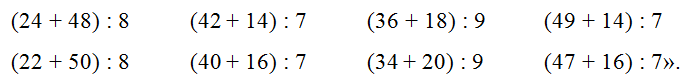
В основе правила лежит закон деления суммы на число:

 «Решите задачу различными арифметическими способами. Установите, какое свойство (правило) является обобще­нием приведенных способов решения данной задачи.

а) Мешок муки имеет массу 50 кг. До обеденного перерыва продали 3 мешка муки, а после перерыва – 5 таких мешков. Сколько килограммов муки продали за весь день? Измените вопрос задачи так, чтобы она стала задачей с лишними дан­ными.

б) На товарную станцию прибыло 2 состава с удобрениями. В одном из них было 27 вагонов, а в другом – 35. Разгрузили 23 вагона. Сколько вагонов с удобрениями осталось разгрузить? Что нужно изменить в условии задачи, чтобы она имела один способ ре­шения, соответствующий этому условию?»

Первая задача имеет следующие способы решения:

I способ: 50 ∙ (3 + 5) = 400 (кг).

II способ: 50 ∙ 3 + 50 ∙ 5 = 400 (кг).

Обобще­нием приведенных способов решения данной задачи является правило умножения числа на сумму: а ∙ (b + c) = a ∙ c + a ∙ c.

Чтобы в задаче появились лишние данные, вопрос может быть сформулирован следующим образом: «Сколько килограммов муки продали до обеденного перерыва?» или «Сколько килограммов муки продали после обеденного перерыва?»

Вторая задача имеет следующие способы решения:

I способ: (27 + 35) – 23 = 39 (вагонов).

II способ: (27 – 23) + 35 = 39 (вагонов).

III способ: (35 – 23) + 27 = 39 (вагонов).

Обобще­нием приведенных способов решения данной задачи является правило вычитания числа из суммы: (а + b) – c = (a – c) + b = a + (b – c).

Чтобы задача имела только один способ решения, можно изменить количество либо разгруженных вагонов (увеличить до числа, большего 35), либо исходных вагонов (уменьшить до числа, меньшего 23).

Организация интегрированной системы самостоятельной работы будущих учителей начальных классов при изучении дисциплин математической направленности способствует повышению качества обучения, развитию их творческого потенциала, стремлению к непрерывному получению новых знаний, профессиональной самореализации, что полностью отвечает требованиям к результатам основных образовательных программ бакалавриата, предъявляемым ФГОС ВПО.