Библиографические ссылки
Факирска Й. Особености във възпитанието и развитието на децата от домовете за деца от предучилищна възраст. – София. - 1997.
Петкова И. Груповата работа с деца от 3 до 7 години, отглеждани и възпитавани в дом за деца, като условие и фактор за ресоциализация. Автореферат. София. 2009.
Дичева Е. Система за превантивно възпитателна работа с трудните деца от предучилищна и начална училищна възраст. Сб. «Превантивната педагогика като научно познание» 1-2 част, СУ «Св. Климент Охридски», Факултет педагогика. София. 2003.
Изменение и допълнение на Закона за народната просвета, Д.В., бр.105/2006.
Петкова И., Иванова К., Братанова Г., Росманова И. Наръчник на обучители. Формиране на умения за независим живот за деца от 3 до 7 години. «Фабер» Велико Търново. 2012.
Активността на детето в детската градина. Книга за учителя – ръководство за планиране / Под редакцията на Н. Витанова. София. 1995.
РАЗДЕЛ II
СОДЕРЖАНИЕ И ТЕХНОЛОГИИ НАЧАЛЬНОГО
ЕСТЕСТВЕННО-МАТЕМАТИЧЕСКОГО
ОБРАЗОВАНИЯ
А.П. Сманцер, Т.В. Гуляева
Белорусский государственный педагогический университет
им. Максима Танка,
г. Минск
a.smantser@mail.ru, hulyaevam@mail.ru
ПЕДАГОГИЧЕСКИЕ АСПЕКТЫ ВОСПИТАНИЯ У
МЛАДШИХ ШКОЛЬНИКОВ ИНТЕРЕСА К
МАТЕМАТИКЕ
_______________________________________________________
В статье акцентируется внимание на воспитании у младших школьников интереса к математике на основе включения в содержание элементов занимательности. Рассматривается роль математических задач, в том числе и логических, в развитии творческого мышления, приводятся примеры логических задач, даются рекомендации по их использованию в образовательном процессе начальной школы.
Ключевые слова: младшие школьники, интерес, занимательность, логические задачи, блоки логических задач, логическое мышление.
Проблема развития интереса к изучению математики является одной из актуальных для педагогической науки. Интерес к предмету способствует формированию у учащихся потребности учиться, получать знания по математике, побуждает их к творческой деятельности, развитию логического мышления.
Интерес к математике подкрепляется содержанием учебного материала, включением в него новых, неизвестных фактов, поражающих воображение учащихся, вызывающих у них удивление. Весьма продуктивным является включение в содержание образования исторических экскурсов о жизни и деятельности выдающихся математиков, интересных историй из их жизни. При этом важно, чтобы учебный материал по содержанию опирался на прошлые знания учащихся, был им интересен и вел к овладению новыми знаниями. Для возбуждения интереса к изучаемому материалу он должен быть отчасти новый, отчасти знакомый учащимся, ибо, как подчеркивал известный русский педагог КД. Ушинский: «Внутренняя занимательность преподавания основана на том законе, что мы внимательны к тому, что надо для нас, но не настолько ново, чтобы быть совершенно незнакомым и поэтому непонятным; новое должно дополнять, развивать или противоречить старому, словом быть интересным, благодаря чему оно может войти в любую ассоциацию с тем, что уже известно» [1, с. 298]. Однако новизну содержания учебного материала невозможно использовать как единственный и постоянный стимул для развития интереса учащихся к математике, имеются и другие действия, вызывающие у них интерес к математике.
Педагогическая практика и наш опыт работы с младшими школьниками показали, что элементы занимательности на уроках математики вызывают у них живой интерес к процессу познания. Одним из средств воспитания интереса к математике является решение задач с интересными фабулами. Необычная задача, часто со сказочным сюжетом, вызывает у учащихся удивление, стремление заглянуть вперед, помогает усвоить математический материал.
Большое значение для развития интереса у школьников к математике имеет сам процесс решения задач, организовывать который следует так, чтобы учащиеся могли испытать чувство эмоционального удовлетворения от сделанного, радость победы над преодоленными трудностями, счастье познания нового, интересного. Важно, чтобы они научились оценивать результаты деятельности при решении задач, тем самым рассматривая задачи и процесс их решения как ценность.
Роль задач в обучении математике очень разнообразна и сложна; решение задач является и средством, и результатом обучения. Задачи используются и для мотивации изучения того или другого раздела, и для выработки навыков вычислений и преобразований, и для развития мышления и пространственного воображения, и для показа применения знаний, и для других целей, среди которых важное место занимает использование задач для воспитания интереса к изучению математики. Не случайно К.Д. Ушинский писал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе с тем занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая и статистическая тема и упражнения в языке» [2, с. 298].
Содержание задач – важный осознанный источник возникновения у школьников интереса их решению. Наши исследования показали, что в младших классах средней школы для воспитания интереса к математике большое значение имеют задачи с необычным и сказочным содержанием. В книге «Сердце отдаю детям» педагог В.А. Сухомлинский приводит массу примеров, как задачи со сказочной фабулой вызывали интерес у учащихся к решению задач. При этом В.А. Сухомлинский практиковал решение задач в процессе отдыха, похода в лес, поле.
Особое место в обучении младших школьников занимают математические логические задачи.
Математические логические задачи – это особый тип задач, способствующий развитию логического мышления ребенка, его умений осуществлять анализ и синтез, аналогию, конкретизацию и обобщение, классифицировать объекты по различным основаниям, наблюдать, сравнивать, проводить аргументированный поиск решения и делать обоснованные выводы. Логические задания ориентированы на развитие общих математических способностей детей младшего школьного возраста, рост их интеллектуального потенциала, активизацию познавательной деятельности, формирование умений и навыков самостоятельной работы. Каждое логическое задание содержит свою «изюминку», свой «секрет». Чтобы его найти и решить задачу, необходимо определить закономерность (правило), по которому составлено условие задания, и применить аналогии. Так, например, задания известных тестов Г. Айзенка и Дж. Равена, в которых нужно увидеть закономерности изменения сразу нескольких признаков, без труда выполняются детьми пяти-десяти лет и вызывают определенные трудности для детей более позднего возраста и для подавляющего большинства взрослых.
Развитие творческого мышления ребенка соответствует инновационной модели обучения и требует от педагога тщательного соблюдения баланса между логикой и интуицией, словом и наглядным образом, дискуссией и инсайдом, осознанным и подсознательным. Решение логических задач способствует закреплению у ученика его умений оперировать теоретическими знаниями не только в стандартных, но и в незнакомых ситуациях; формирует такие приемы умственной деятельности, как анализ, синтез, обобщение, классификация, выделение существенных признаков и др.; развивает навыки нахождения скрытых закономерностей в построении логических схем и наблюдаемых явлений; стимулирует его познавательную активность, способность к самоорганизации; предполагает наличие определенных личностных качеств – внимание, наблюдательность, настойчивость в достижении цели, целеустремленность, усидчивость, терпение.
Мы выделяем несколько блоков логических задач. Так, задачи пропедевтического, подготовительного уровня являются наиболее простыми и их целесообразно решать с помощью конкретных действий: дорисовать, обвести, закрасить, показать стрелочкой и т.д. Они предназначены для детей старшего дошкольного возраста. Также разработаны логические задачи четырех уровней для 1-4 классов. При этом от уровня к уровню задания усложняются.
Логические задачи могут быть использованы учителями математики в качестве дополнительных развивающих материалов при проведении уроков математики, занятий по интересам и организации кружковой и факультативной работы, при составлении разнообразных индивидуализированных реконструктивно-вариативных заданий, а также самими учащимися для самостоятельного решения в свободное время.
Приведем образцы решения некоторых логических задач, которые предлагались детям в дошкольных образовательных учреждениях.
Задача 1. Нарисуй пропущенный рисунок.
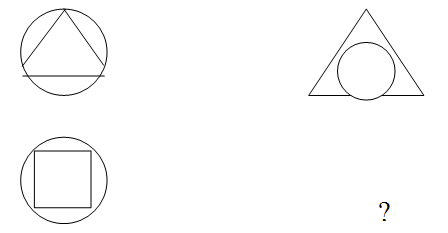
Если рассмотреть эту задачу по вертикали, то, исследуя левый вертикальный столбец, замечаем, что в первом круге нарисован треугольник, а во втором – квадрат, т.е. треугольник заменен квадратом. Рассматривая правый вертикальный столбец, видим, что в треугольнике нарисован круг. Рассуждая по аналогии с левым столбцом, делаем вывод, что треугольник надо заменить квадратом. Таким образом, нужно нарисовать квадрат, а в нем – круг.
Эта задача имеет и другую стратегию поиска решения – рассуждения по горизонтали: в первом ряду поменялись местами треугольник и круг. Поэтому и во втором ряду поменяем местами квадрат и круг и получим тот же ответ.
Задача 2. Вставь пропущенное число.
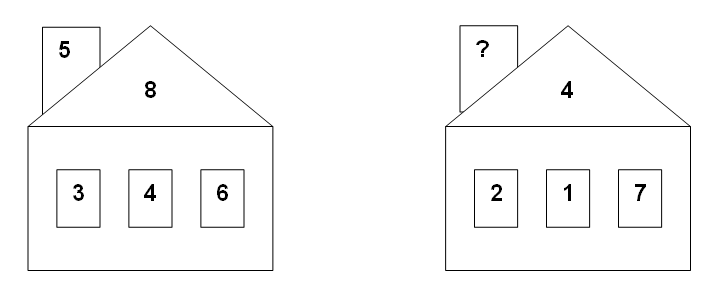
Начинаем решение с поиска закономерностей, записанных в домике слева. Замечаем, что сумма чисел, записанных в проемах окон (3+4+6=13), равна сумме чисел, расположенных в верхней части дома (5+8=13). Воспользуемся этой закономерностью в правом домике: имеем ?+4=2+1+7, т.е. искомое число равно 6.
Приведем следующее логическое упражнение, являющееся примером составления разнообразных вариативных заданий.
Задача 3. Определите пропущенное число.
Рассматривая числа, записанные на игрушках левой елочки, можно заметить, что сумма чисел на ветвях каждого ряда одинакова: 1+9=10, 2+8=10, 3+7=10, 4+6=10. Следовательно, сумма всех чисел на игрушках будет 1+2+3+4+5+6+7+8+9=45.Таким образом, число, записанное на стволе елки, равняется сумме чисел, записанных на всех ветвях и верхушке.
Эту логическую закономерность используем по аналоги для вычисления значения суммы чисел на стволе правой елочки. Так, сумма чисел, записанных на ветвях и верхушке, будет 2+3+4+5+6+7+8+9+10 . Для быстрого и рационального нахождения значения этой суммы можно использовать группировки чисел, как и на левой елочке, т. е. 2+8=10, 3+7=10, 4+6=10 и остается найти значение суммы 10+10+10+5+9+10. Можно было сгруппировать числа и иначе: (2+10)+ (3+9)+ (4+8)+ (5+7)+6.
Поскольку существуют и другие способы группировки чисел, способствующие быстрому нахождению значения суммы, целесообразно предложить учащимся попробовать найти их. Можно найти и иные варианты решения данного примера. Например.
1. Не выполняя сложения чисел, записанных на правой елке, найти их сумму, если сумма чисел на левой елке равна 45. Опираясь на то, что 1+2+3+4+5+6+7+8+9=45 , и, сравнивая числа, записанные на левой и правой елках, можно заметить, что каждое соответствующее число правой елки на единицу больше, чем число с левой елки. Таких чисел 9, т. е. сумма чисел, записанная на правой елке, будет 45+9=54.
2. Сравнивая сумму чисел на левой елке 1+2+3+4+5+6+7+8+9=45 и сумму чисел на правой елке 2+3+4+5+6+7+8+9+10, заметим, что во второй сумме отсутствует число 1, зато есть число 10, которое отсутствует в первой сумме. Значит, значение второй суммы будет 45-1+10=54.
Задача 4. Напиши зашифрованное слово.
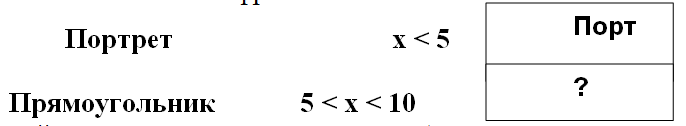
В первой строке задания пронумеруем буквы в слове «портрет». Так как x<5, это значит, что x∈{1;2;3;4}. А это означает, что решением неравенства x<5, являются четыре первые буквы, образующие закодированное слово «порт».
Рассуждаем аналогично во второй строке задания. Решение неравенства 5<x<10 есть x∈{6;7;8;9}. Таким образом, из слова «прямоугольник» выбираем буквы с порядковыми номерами 6, 7, 8, 9 и получаем закодированное решение этого неравенства в виде слова «угол».
Задача 5. Напиши недостающее число.
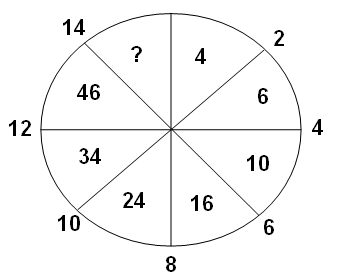
Начиная с числа 4, пытаемся выяснить, на сколько одно число больше другого. Например, на сколько число 6 больше числа 4; на сколько число 10 больше числа 6 и т.д. С этой целью выполним вычитание: 6-4=2; 10-6=4; 16-10=6; 24-16=8; 34-24=10; 46-34=12.
Анализируя полученные результаты и сравнивая их, находим закономерность: второе число больше первого на 2, третье больше второго на 4, следующее больше предыдущего на 6, на 8, на 10 и на 12. Следовательно, искомое число будет на 14 больше, чем 46, т. е. это число будет 60, так как 60=46+14.
Полученные результаты можно проанализировать и иначе. Числа 2, 4, 6, 8, 10, 12 – последовательные и четные. Следовательно, следующим числом за числом 12 будет число 14. Значит, искомое число больше 46 на 14. То есть искомое число равно 60. Мы получили тот же ответ.
Мир математических логических задач разнообразен и богат. Однако прежде чем предлагать ученикам задание для самостоятельного решения, необходимо рассмотреть хотя бы одно аналогичное задание со всем классом, объяснить его составные части и пути поиска решения.
Важно показать учащимся, в чем «изюминка», «секрет» предложенного задания. Поскольку именно наличие «секрета» способствует развитию познавательного интереса учащихся, их творческих способностей и исследовательских умений, а создание на уроке проблемной ситуации позволяет держать в напряжении мыслительную деятельность учащихся.
Следует обратить внимание учащихся, что многие математические задачи имеют несколько вариантов решений в зависимости от выбранной закономерности.
Таким образом, умение решать задачи является одним из показателей уровня математического развития детей, глубины усвоения ими математического материала. Регулярное использование на уроках математики разнообразных задач, в том числе и логических, воспитывает у школьников интерес к изучению математики, расширяет их математический кругозор, способствует математическому развитию.