2.4.Определение средней разности температур

Простейшими и распространенными схемами теплообмена являются прямоток и противоток (рис.2.1).

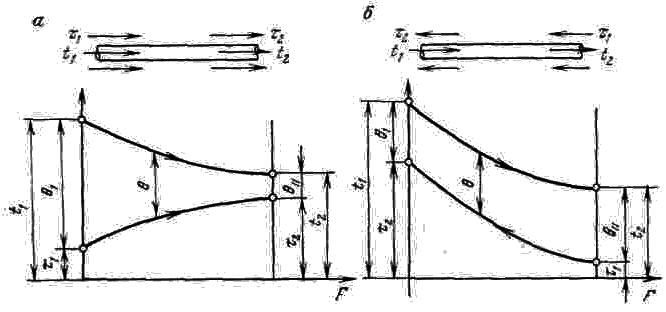
Рис.2.1. Температурные диаграммы для прямотока (а) и противотока (б)

Уравнение теплового баланса для элементарного участка поверхности теплопередачи теплообменников этих схем (при отсутствии тепловых потерь) формулируется следующим образом

(а)

где –количество теплоты в единицу времени, пройденное через стенку; – количество теплоты, отданное нагревающим потоком; – количество теплоты, полученное нагреваемым потоком.

Знаки в уравнении теплового баланса (а) определяются принятым направлением отсчета – направлением движения нагревающего потока; в связи с этим верхние знаки относятся к прямотоку, нижние – к противотоку.

Выделим из исходного дифференциального уравнения баланса теплопередачи (а) изменения температуры нагревающего и нагреваемого потоков

(б)

(в)

Вычитая из первого (б) выражения второе (в), получим

(г)

или

(д)

Отсюда непосредственно следует следующее преобразованное выражение баланса теплопередачи на элементарном участке:

(е)

где – текущая разность температур нагревающего и нагреваемого потоков; –приведенный эквивалент обоих потоков

(ж)

Поделив переменные в преобразованном уравнении (е), получим

(з)

Таким образом, первое интегральное соотношение после интегрирования выражения (з) имеет вид

(и)

Второе интегральное соотношение получается при непосредственном интегрировании исходного уравнения баланса теплопередачи (е)

(к)

Сопоставляя оба интегральных соотношения (и) и (к), получим расчетное уравнение для средней разности температур

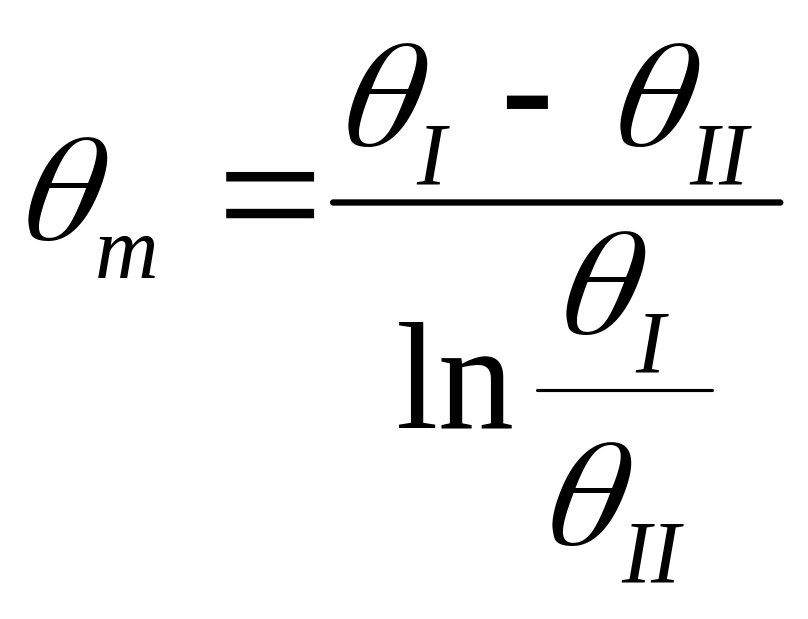(2.9)

Значения начальной и конечной разности температур приводятся в табл. 2.1.

Выражение средней разности температур (2.9) действительно для

прямотока и противотока и называется уравнением (формулой) Грасгофа.

Таблица 2.1.

Значения начальной и конечной разности температур

Разности температур	Схема теплообмена
	Прямоток		Противоток

2.5.Обобщенное уравнение теплового баланса в формулировке н.И.Белоконя

Наиболее общими уравнениями теплопередачи при переменных температурах, действительными для любой схемы теплообмена, являются уравнения, предложенные Н.И. Белоконем. Эти уравнения позволяют проводить как расчеты I рода, так и расчеты II рода на основе стабильной характеристики схемы теплообмена – индекса противоточности Р.

Количество передаваемой теплоты в единицу времени может быть определено или из уравнения теплового баланса (в расчетах I рода), или из уравнения Н.И. Белоконя (в расчетах II рода)

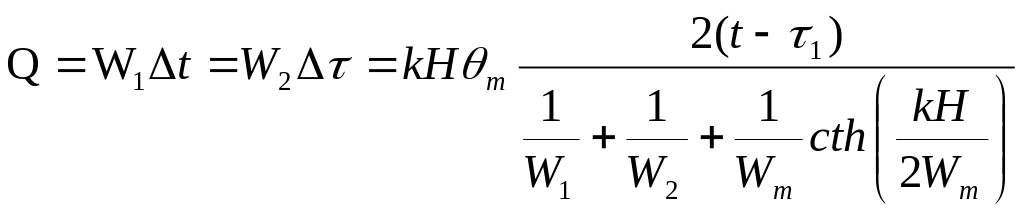(2.10)

где – средняя разность температур для любой схемы теплообмена,

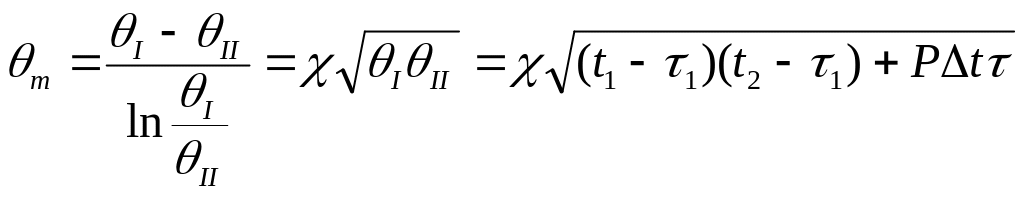(2.11.)

– приведенный эквивалент обоих потоков

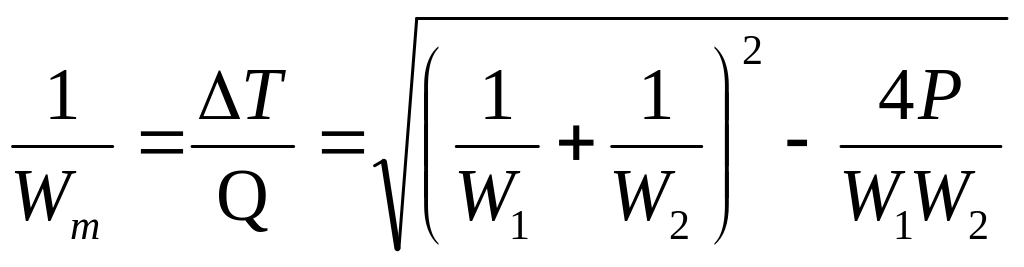(2.12)

– характеристическая разность температур

, – наибольшая ( ) и наименьшая ( ) разности температур процесса теплопередачи,

(2.13)

(2.14)

– средняя арифметическая разность температур процесса теплопередачи, независящая от схем теплообмена,

(2.15)

– коэффициент, характеризующий соотношение средних – логарифмической и геометрической,

Потери от наружного охлаждения теплообменного аппарата могут быть учтены путем соответствующего изменения величины , передающего теплоту в окружающую среду

; (2.16)

или

; (2.17)

Индекс противоточности Р является основной характеристикой схемы теплообмена при переменных температурах. Физическое содержание индекса противоточности можно уяснить из анализа схемы теплообмена теплообменного аппарата с U-образными трубками (рис. 1); причем любой теплообменный аппарат по конечному эффекту можно заменить теплообменным аппаратом с U-образными трубками.

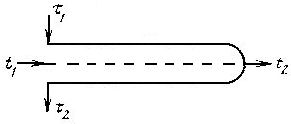
Рис. 2.2. Схема элемента теплообменного аппарата с U-образными трубками

Индекс противоточности в этом случае можно представить как отношение комплекса kH противоточной части к общему значению комплекса kH всего теплообменного аппарата

(2.18)

Тогда легко можно получить значения индекса противоточности для важнейших простейших схем теплообмена – противотока Р=1 и прямотока Р=0. Значения индекса противоточности для наиболее распространенных схем теплообмена приводятся в табл.2.2.

Для сложных симметричных схем теплообменных аппаратов, состоящих из участков противоточного, прямоточного и пере-крестноточного токов, индекс противоточности достаточно точно может быть подсчитан по принципу аддитивности

,

где – значения индекса противоточности и комплекса i-го участка сложной схемы теплообмена; kH –неразделимый комплекс всего теплообменного аппарата.

Для экспериментального определения индекса противоточности может быть использовано уравнение связи его с относительной величиной средней разности температур

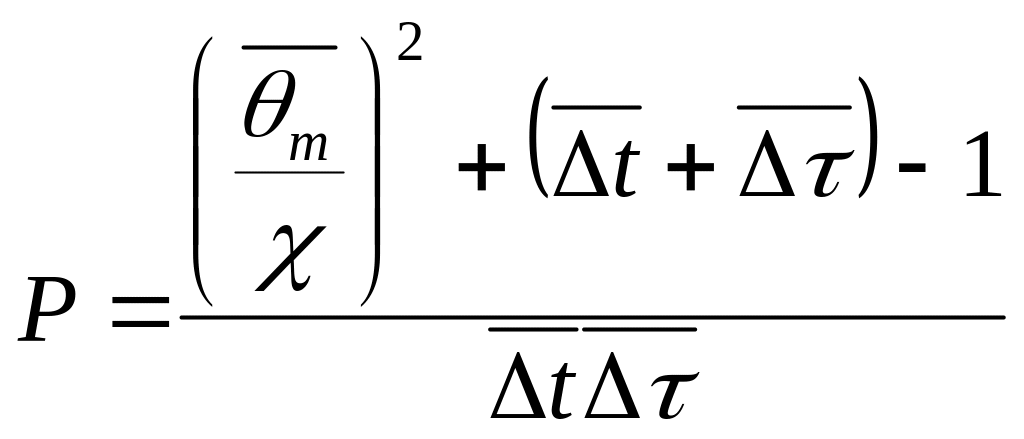(2.19)

где – средняя разность температур процесса теплопередачи, отнесенная к разности начальных температур;

; – отношения перепадов температур нагревающего и нагреваемого теплоносителей к разности начальных температур.

Выбор схемы теплообменного аппарата можно осуществить исходя из следующих соображений. Чем меньше значение средней разности температур, тем больше величина комплекса (kH) для теплообменного аппарата. В пределе, когда средняя разность температур приближается к нулю, потребуется бесконечно большой комплекс (kH)

теплообменного аппарата ( ).

Таблица2.2.

З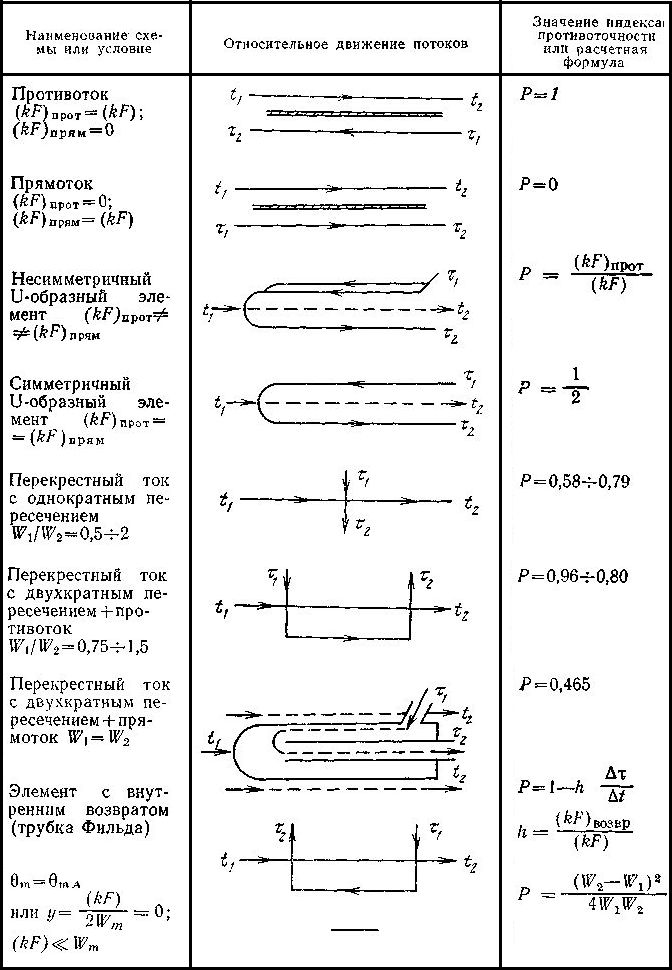 начения индекса противоточности для наиболее распространенных схем теплообмена (в таблице произведена замена обозначений согласно первоисточнику –F площадь поверхности теплопередачи

Средняя разность температур может быть равна нулю, если . Подставляя в (2.13, 2.14) значения из (2.15) и - характеристическую разность температур, получим минимальный индекс противоточности:

(2.20)

Таким образом, при минимальном значении индекса противоточности и значениях его меньше минимального не может быть реализован заданный температурный режим. Следовательно, основным условием получения заданных температур теплоносителей при выборе схемы теплообменного аппарата является превышение ее индекса противоточности Р над минимальным его значением , т.е. .Чем больше разность и , тем эффективнее схема теплообмена.

Расчетное уравнение (2.10) можно несколько упростить, исключив из него гиперболический котангенс. Функция

четная и может быть разложена в ряд

Соответственно может быть переписано уравнение (2.10)

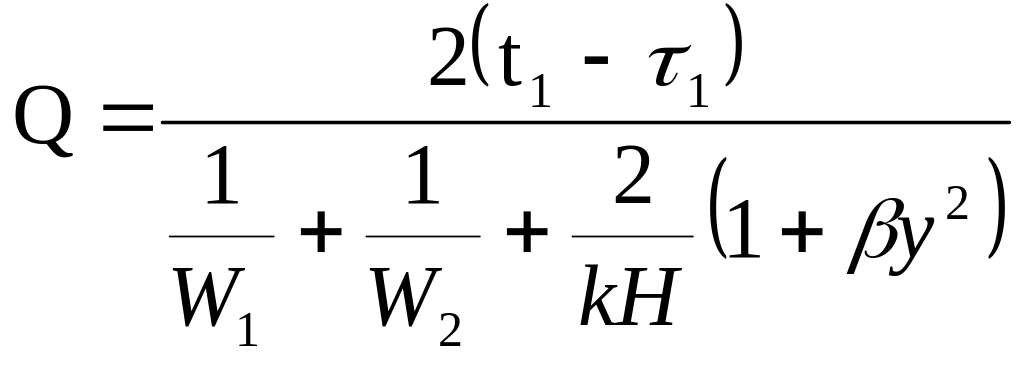(2.21)

Причем

;

Значение коэффициента в формуле (2.21)

	0	0,5	1,0	1,5	2,0
	0,3333	0,3279	0,3130	0,2921	0,2687

В связи со стабильностью значений в технических расчетах можно принять .