2.2. Теплопередача между двумя теплоносителями через разделяющую их стенку

Передача теплоты от одной подвижной среды (жидкости или газа) к другой через разделяющую их твердую стенку любой формы называется теплопередачей. Именно этот процесс реализуется в рекуперативных теплообменных аппаратах (ТА).

Расчетная формула теплопередачи для стационарного режима имеет следующий вид:

Q=кH(t_ж1t_ж2). (2.2)

Для однослойной плоской стенки коэффициент теплопередачи определяется следующим образом:

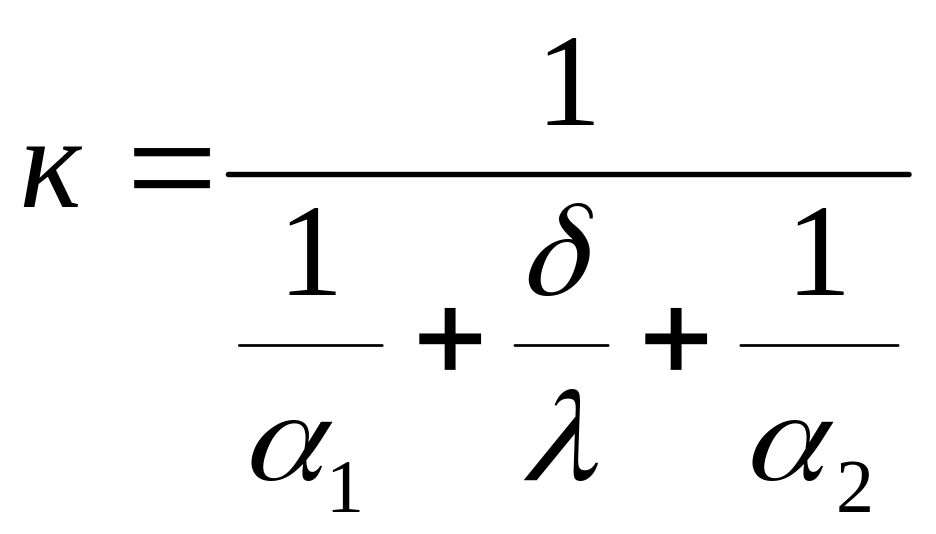. (2.3)

где α₁ и α₂ - соответственно внутренний и внешний коэффициенты теплоотдачи (Вт/м² К), λ- коэффициент теплопроводности материала стенки (Вт/м К), δ-толщина стенки (м).

Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи:

. (2.4.)

Для многослойной плоской стенки коэффициент теплопередачи для стационарного теплового режима следующий:

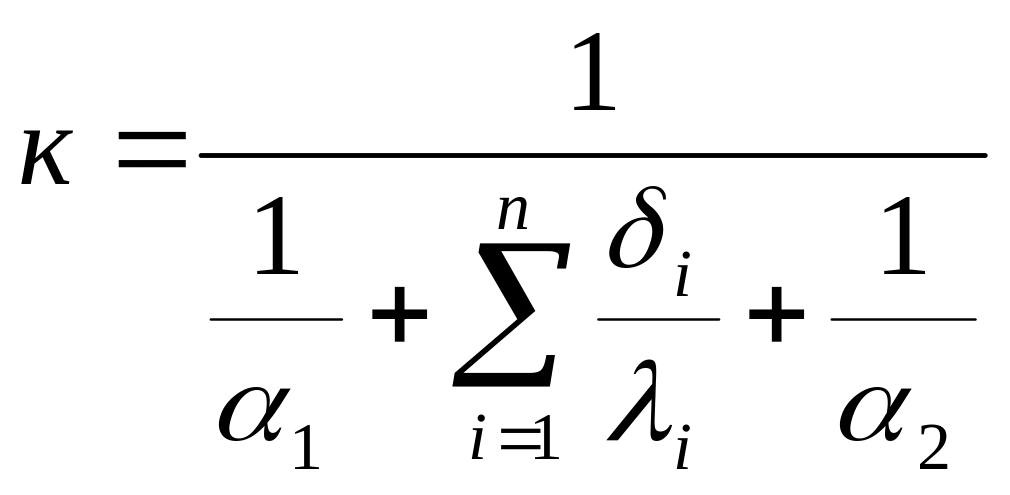, (2.5)

где — термическое сопротивление многослойной стенки.

Для многослойной цилиндрической стенки линейный коэффициент теплопередачи определяется:

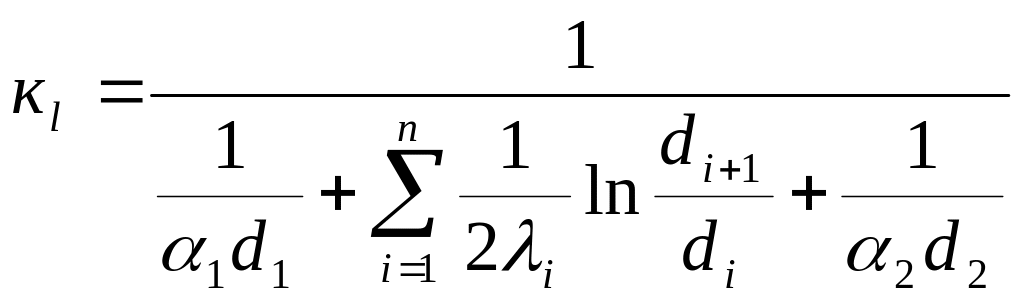. (2.6)

Величина к_l называется линейным коэффициентом теплопередачи, который численно равен количеству теплоты, проходящей через стенку трубы длиной в 1 м в единицу времени при разности температур между горячей и холодной средами в 1˚С.

2.3. Оптимизация (регулирование) процесса теплопередачи

В технике встречаются два вида задач, связанных с регулированием процесса теплопередачи. Один вид задач связан с необходимостью уменьшения количества передаваемой теплоты (тепловых потерь), т. е. с необходимостью введения в конструкцию устройств тепловой изоляции. Другой вид задач связан с необходимостью увеличения количества передаваемой теплоты, т. е. с интенсификацией теплопередачи. Из уравнения (2.2) следует, что количество передаваемой теплоты (при t_ж1=idem и t_ж2=idem) зависит от значения (кН).

При изоляции поверхностей любой геометрической формы задача в заключительной части решается технико-экономическим расчетом. Однако при изоляции криволинейных поверхностей имеются некоторые технические особенности. Термическое сопротивление, отнесенное к 1 м длины трубы, определяется из уравнения

(2.7)

При ₁=idem; d₁=idem; =cоnst; ₂=idem полное термическое сопротивление теплопередачи будет зависеть от внешнего диаметра трубы d₂. Из выражения для R_l (2.7) следует, что =idem; тепловое сопротивление увеличивается с возрастанием d₂; тепловое сопротивление уменьшается с увеличением d₂. Полное термическое сопротивление R_l зависит от характера изменения составляющих R_lc и R_l2.

Чтобы выяснить, как будет изменяться R_l при изменении толщины цилиндрической стенки, исследуем R_l как функцию d₂. Возьмем производную от R_l по d₂ и приравняем нулю:

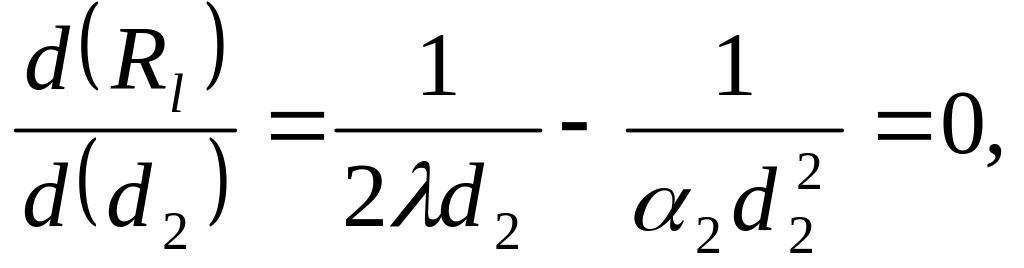
отсюда d₂=d_кр=2/₂, (2.8)

где d_кр — критический диаметр, м.

Значение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи, называется критическим диаметром.

В интервале d₂d_кр полное термическое сопротивление теплопередачи падает с увеличением d₂; это объясняется тем, что увеличение наружной поверхности трубы оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки.

В интервале d₂d_кр полное термическое сопротивление теплопередачи увеличивается с ростом d₂ из-за преобладающего влияния на R_l толщины стенки. Эту особенность изоляции криволинейных поверхностей различных аппаратов необходимо учитывать при выборе вида тепловой изоляции.

При наложении слоя тепловой изоляции на цилиндрическую поверхность полное термическое сопротивление теплопередачи определяется из выражения (2.7).

Удельные тепловые потери получим:

(а)

Из выражения (а) следует, что q_l при увеличении внешнего диаметра изоляции d₃ сначала будет возрастать и при d₃=d_кр будет иметь максимальное значение. При дальнейшем увеличении внешнего диаметра изоляции q_l будет снижаться.

Материал изоляции выбирается следующим образом: по заданным значениям ₂ и _из определяют d_кр из выражения (2.8). Если окажется, что d₃d_кр, то применение выбранного материала в качестве тепловой изоляции нецелесообразно. Для целесообразного выбора изоляции необходимо соблюдение условия , а . Из приведенного неравенства следует, что чем меньше диаметр изолируемого трубопровода, тем меньше должен быть коэффициент теплопроводности изоляционного материала — _из, т. е. качество изоляции должно быть выше. Аналогично решается задача при изоляции сферических поверхностей.

При интенсификации теплопередачи в соответствии с основным уравнением теплопередачи (2.2) необходимо по возможности увеличить кН, но изменять по желанию температуру сред (t_ж1, t_ж2) зачастую не позволяют условия технологического процесса, неэкономичность и другие причины.

Повысить значение кН можно путем увеличения коэффициента теплопередачи, расчетной площади поверхности теплопередачи в отдельности и одновременно.

Для чистой однослойной стенки выражение коэффициента теплопередачи из выражения (2.5) имеет вид

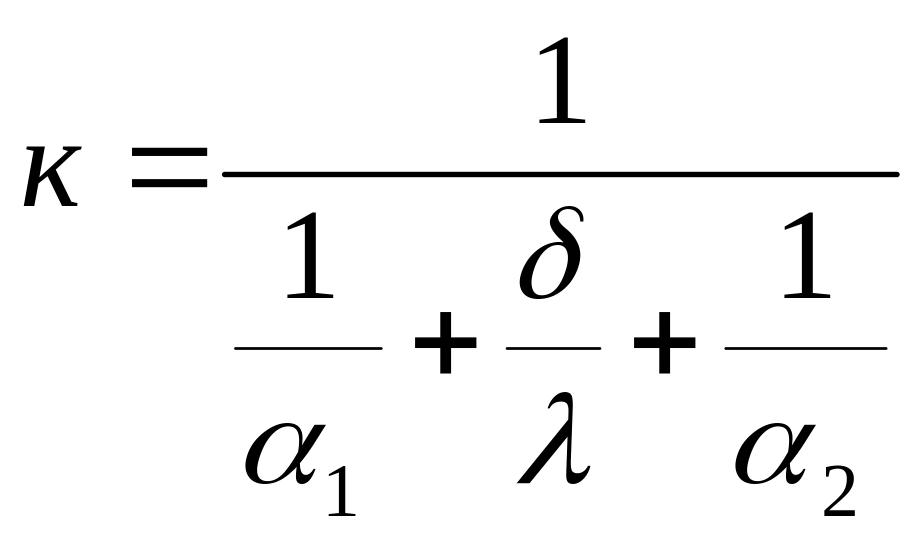. (б)

Термическое сопротивление теплопроводности металлической стенки мало lim(δ/λ)0, и им можно пренебречь, тогда

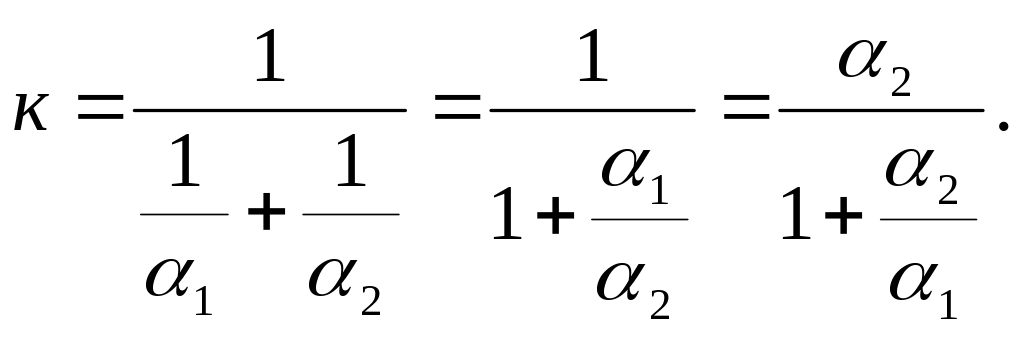(в)

Из этого уравнения следует, что если ₂₁, то к₁ и если ₁₂, то к₂, т. е. коэффициент теплопередачи всегда меньше минимального значения коэффициента теплоотдачи.

В соответствии с уравнением (в) и выводом для увеличения коэффициента теплопередачи необходимо повышать минимальный коэффициент теплоотдачи. Если ₁₂, то «к» можно увеличить за счет увеличения любого .

Для указанной однослойной металлической стенки

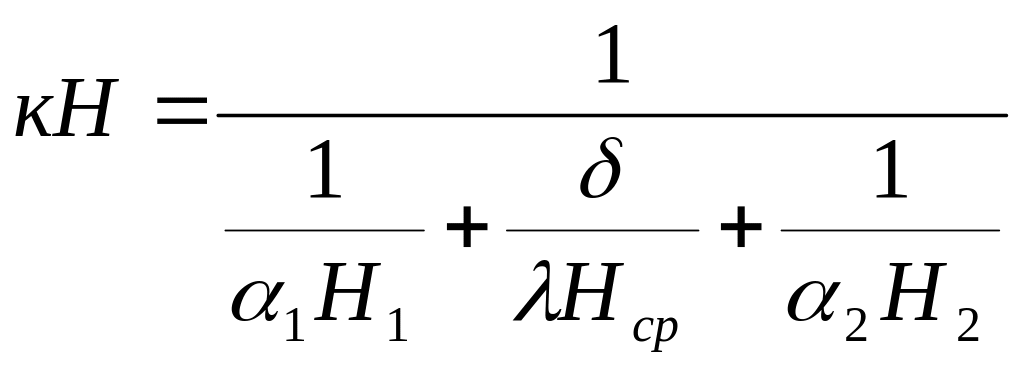, (г)

и соответственно запишется выражение общего термического сопротивления теплопередачи:

(д)

Естественно, чем меньше общее термическое сопротивление, тем больше значение «кН», интенсивнее процесс теплопередачи.

Значение термических сопротивлений и зависит не только от величин ₁ и ₂, но и от размеров площадей поверхностей Н₁ и Н₂. Следовательно, если  мало, то термическое сопротивление теплоотдачи можно уменьшить, увеличивая соответствующую площадь поверхности. Таким образом, для уменьшения общего термического сопротивления необходимо уменьшать наибольшее термическое сопротивление, т. е. увеличивать ту площадь поверхности, со стороны которой  меньше. Увеличение площади поверхности теплоотдачи достигается путем ее оребрения.