5. Дан ряд распределения случайной величины :

	1

. Математическое ожидание , дисперсия . Найти значение случайной величины

6. В урне 2 белых и 1 черный шар. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина – количество извлеченных белых шаров. Записать ряд распределения случайной величины.

7. Игральную кость бросают 54 раз. Случайная величина – количество выпавших «троек» и «шестерок». Найти дисперсию случайной величины.

8. Дана функция плотности распределения вероятностей случайной величины : Найти значение параметра .

9. Случайная величина распределена по равномерному закону на отрезке . Найти среднее квадратичное отклонение случайной величины.

10. Случайная величина распределена по экспоненциальному закону с параметром . Записать функцию распределения вероятностей случайной величины.

11. Случайная величина распределена по экспоненциальному закону с параметром . Найти математическое ожидание случайной величины.

12. Случайная величина распределена по экспоненциальному закону с параметром . Найти вероятность попадания случайной величины в интервал

13. Закон распределения случайной величины задан функцией плотности . Найти дисперсию случайной величины.

14. Функция плотности распределения вероятностей случайной величины имеет вид . Найти точки перегиба кривой Гаусса

Типовые расчеты по разделу «Теория случайных величин» Вариант 4

1 . Дан графический закон распределения дискретной случайной величины (многоугольник распределения). Записать ряд распределения случайной величины.

2. Дискретная случайная величина принимает значения -1, 1, 2 с соответствующими вероятностями , 0,5, 0,3. Найти математическое ожидание случайной величины.

3. Дан ряд распределения случайной величины:

	-2		6
		0,3	0 ,4

Найти моду случайной величины .

4. Дан график функции распределения случайной величины

со значениями и . Найти вероятность значения

	2

5. Дан ряд распределения случайной величины :

.

Математическое ожидание , дисперсия . Найти значение вероятности .

6. В урне 2 белых и 4 черных шара. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина – количество извлеченных белых шаров. Записать ряд распределения случайной величины.

7. Игральную кость бросают 36 раз. Случайная величина – количество выпавших «двоек». Найти дисперсию случайной величины.

8. Случайная величина задана функцией распределения

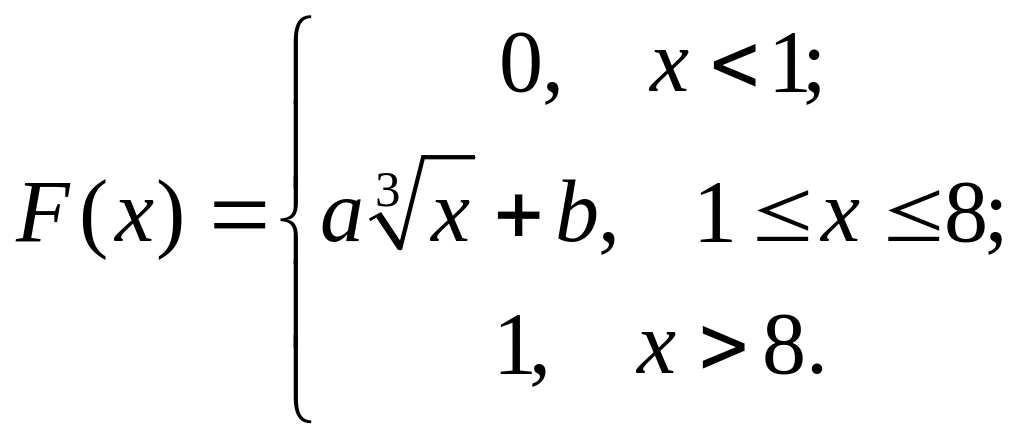
Найти значение параметра .

9. Случайная величина распределена по равномерному закону на отрезке . Найти математическое ожидание случайной величины.

10. Случайная величина распределена по экспоненциальному закону с параметром . Записать функцию распределения вероятностей случайной величины.

11. Случайная величина распределена по показательному закону с параметром . Найти дисперсию случайной величины.

12. Случайная величина распределена по экспоненциальному закону с параметром . Найти вероятность попадания случайной величины в интервал .

13. Закон распределения случайной величины задан функцией плотности . Найти среднее квадратичное отклонение случайной величины.

14. Функция плотности распределения вероятностей случайной величины имеет вид . Найти точки перегиба кривой Гаусса