4.7. Выбор вида модели

Выбор вида модели, наилучшим образом характеризующий существо экономического, производственного, технологического процесса и отвечающий задачам анализа, является важным этапом при принятии управляющего решения.

1. Прежде чем приступить к получению уравнения регрессии, следует провести качественный анализ (отбор фактов исходя из предположения о возможном их влиянии на анализируемый показатель).

2. После проведения предварительного качественного анализа следует приступить к получению уравнения регрессии.

3. Если фактический анализ не позволяет сделать однозначный выбор вида модели, то следует одну и ту же статистику использовать для получения различных уравнений (линейных и нелинейных, однофакторных и многофакторных) и сравнить их между собой по определенным признакам, характеризующим качество подбора модели.

Целесообразно в качестве такого признака принять функцию

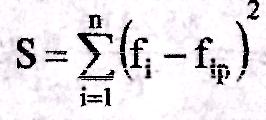
Если сравнивать две или несколько моделей, следует отдать предпочтение той, у которой величина S будет минимальной.

4.7.1. Сравнение величины значений функции s для линейной и параболической регрессий

Для сравнения величины значений функции S для линейной и параболической регрессий, рассчитанных по данным примеров (таблица 4.3,4.4), построим вспомогательную таблицу (таблица 4.5).

Таблица№4.5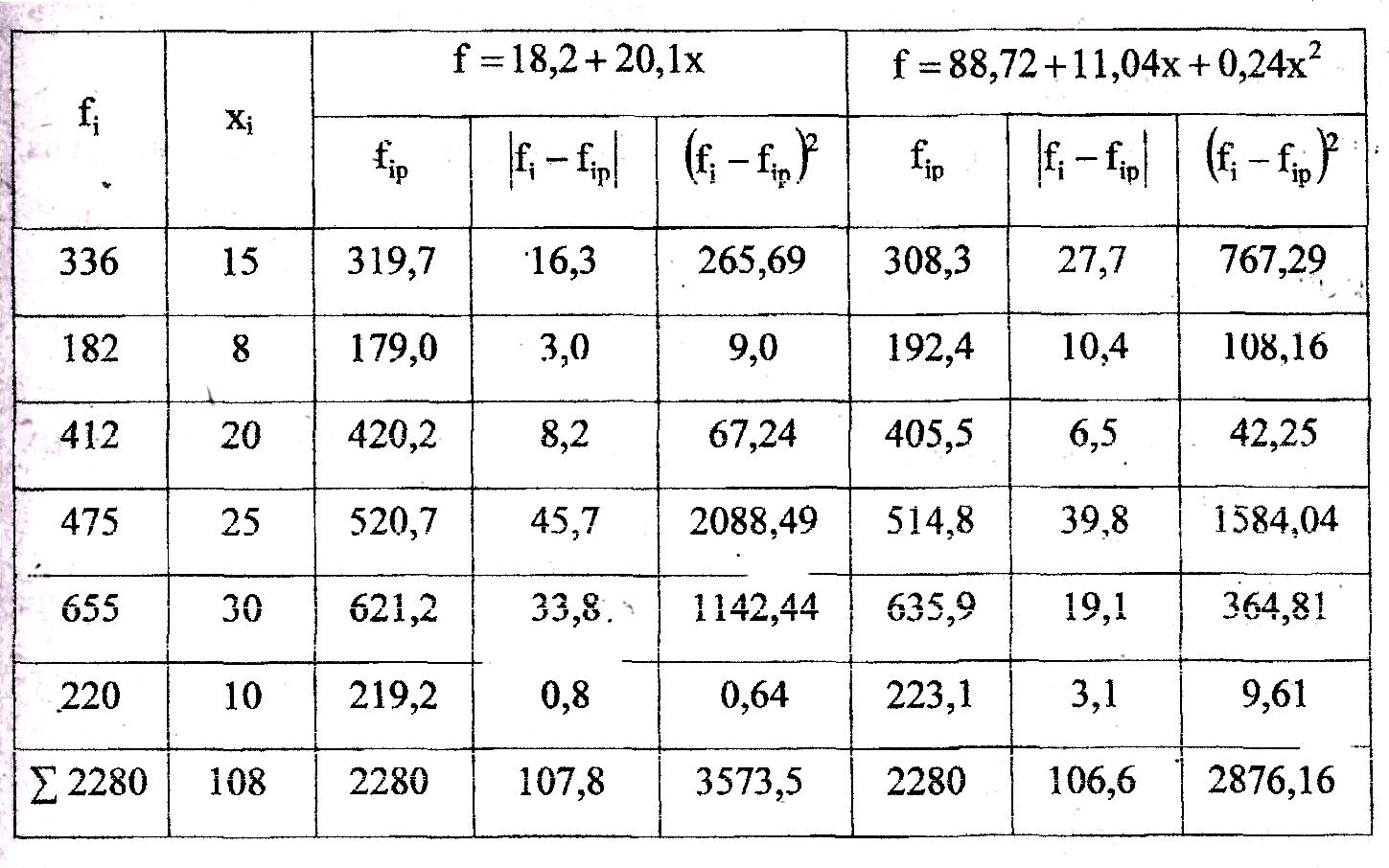

Расчеты показывают, что в данном случае уравнение параболы лучше описывают тенденцию изменения показателя . Однако при окончательном решении вопроса о выборе вида уравнения следует учитывать трудоемкость вычислений и соотносить ее с разностью в величине допустимой погрешности.

Для принятия решения о приемлемости полученного уравнения используются различные критерии,

Средняя относительная ошибка представляет собой отношение суммы абсолютных значений отклонений фактических значений от расчетных к сумме всех значений показателя. Если величина не превышает 15%, то модель считается адекватной реальному процессу.

В нашем случае для линейной

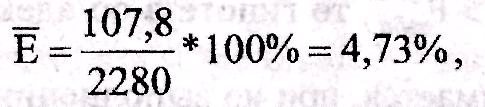регрессии а для параболической прогрессии

Так как линейная регрессия всего на 0,05% дает большую погрешность по сравнению с параболической, ее можно считать вполне пригодной для практического использования.

Критерий Фишера_используется для более строгой оценки соответствия уравнения регрессии реальной статистики, который определяется по формуле:

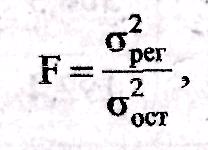
где: - дисперсия регрессии, характеризующая отклонение расчетных значений показателя от его среднего значения;

- остатки дисперсии, характеризующие отклонения фактических значений показателя от расчетных с помощью уравнении регрессии. Значения вычисляются по формулам:

где: - число пар наблюдений ;

- число вычисляемых статистических параметров

Величина характеризует интенсивность показателя при варьировании фактора. Значение является характеристикой плотности расположения точек относительно уравнения регрессии. Расчетное значение - критерия сравнивается с табличным. Если , то гипотеза об адекватности проверяемого уравнения регрессии принимается, при не выполнении этого условия - отвергается. При этом учитывается степень гарантии, с которой можно принять гипотезу о возможности использования проверяемого уравнения регрессии.