4.3. Корреляционный анализ многофакторных линейных и нелинейных моделей

Корреляция - систематическая и обусловленная связь между двумя рядами данных.

Корреляция - связь переменных, при которой одному значению одного признака соответствует несколько значений другого признака, отклоняющегося в ту или иную сторону от своего среднего значения.

Корреляционный анализ многофакторных линейных и нелинейных моделей имеет некоторые особенности. В тех случаях, когда на показатель влияет не один фактор, а несколько, их влияние оценивается через совокупный коэффициент корреляции .

Если показатель f линейно связан с двумя факторами x₁ и x₂ то

совокупный коэффициент корреляции определяется по формуле

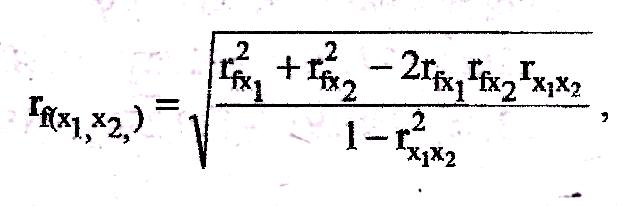
где: - коэффициент парной корреляции между показателем f и факторами х₁ , х₂;

- коэффициент парной корреляции факторов х₁ и х₂ между собой.

В сложных организационно-технических системах, экономических процессах факторы могут быть тесно связаны между собой. Это явление называется мультиколлениарностью.

Если коэффициент парной корреляции между факторами превышает , то это свидетельствует о наличии мультиколлениарности в двухфакторном уравнении регрессии и в этом случае один из факторов следует отбросить.

Вопрос о том, какой фактор следует исключить из уравнения регрессии, решается на основе качественного анализа сложного (экономического, преобразовательного, производственного, технологического) процесса.

Совокупный коэффициент корреляции изменяется от нуля до единицы. Если , то показатель f не может быть связан с х₁ и х₂ линейной корреляционной зависимостью. При этом возможна другая связь, может быть даже функциональная.

Если , то это означает, что связь между , носит линейный функциональный характер.

Во всех других случаях, где совокупный коэффициент корреляции имеет значения от 0 до 1, совокупный коэффициент корреляции является мерой линейной корреляционной связи .

Если в уравнении регрессии не два, а три и более факторов, то совокупный коэффициент корреляции определяется по соответствующим более сложным формулам.

Кроме совокупного коэффициента корреляции важное значение имеют частные коэффициенты корреляции, которые оценивают степень связи показателя с одним из факторов при исключении влияния других.

При линейной двухфакторной зависимости вида частный коэффициент корреляции f и х₁ при исключенном влиянии х₂ будет равен:

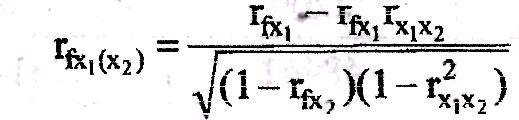
и аналогично оценивается влияние фактора х₂ на f при исключенном х₁:

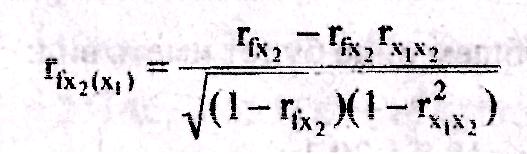
Частные коэффициенты корреляции аналогичны коэффициентам парной корреляции. Они изменяются в пределах (0,1).

Если , то исключается частная связь между , хотя нелинейная корреляционная и даже функциональная связь между ними возможна.

4.4. Однофакторная нелинейная модель

В случаях, когда наибольшее влияние на показатель оказывает один фактор, то связь между ними носит нелинейный характер, используется однофакторная нелинейная модель.

Задача – найти уравнение однофакторной регрессии F.

Для нахождения уравнения регрессии от одного параметра (фактора, переменной) воспользуемся следующей системой двух уравнений:

.

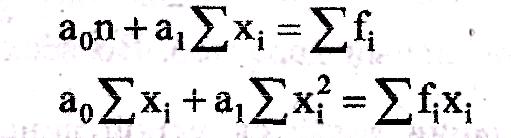По таблице, определяющей как исходные, так и промежуточные показатели для последней системы уравнений, представленной ниже, составим систему уравнений.

Таблица 4.2

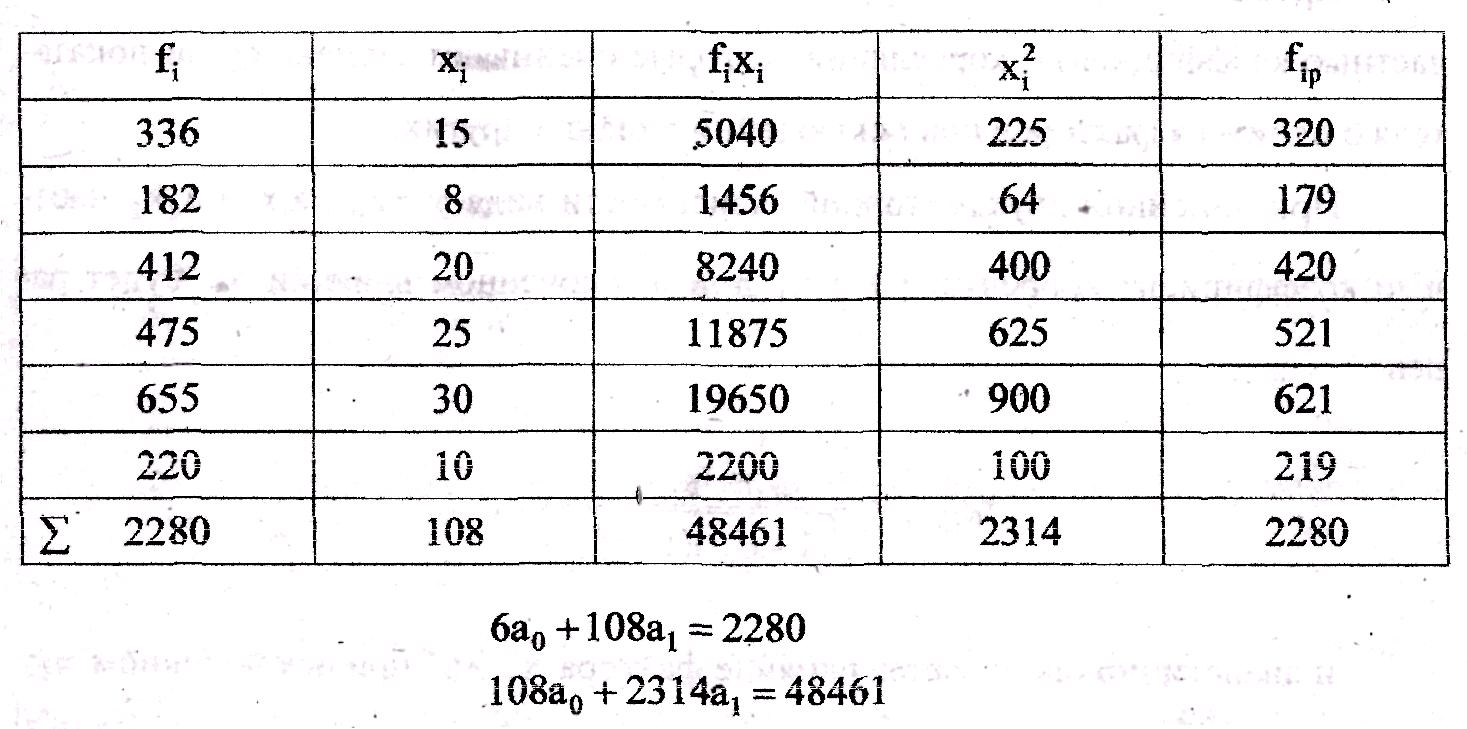
Уравнение связи в общем виде будет иметь вид:

Коэффициент называют коэффициентом регрессии,

коэффициент _- свободным членом уравнения регрессии.