Метод парных сравнений

По сравнению с предыдущими метод парных сравнений обладает пре- имуществом, в нем экспертам предлагается произвести сравнение вариантов (факторов, признаков) попарно, с тем чтобы установить в каждой паре наиболее важный. Варианты сопоставляются попарно, а затем выбирается один из них.

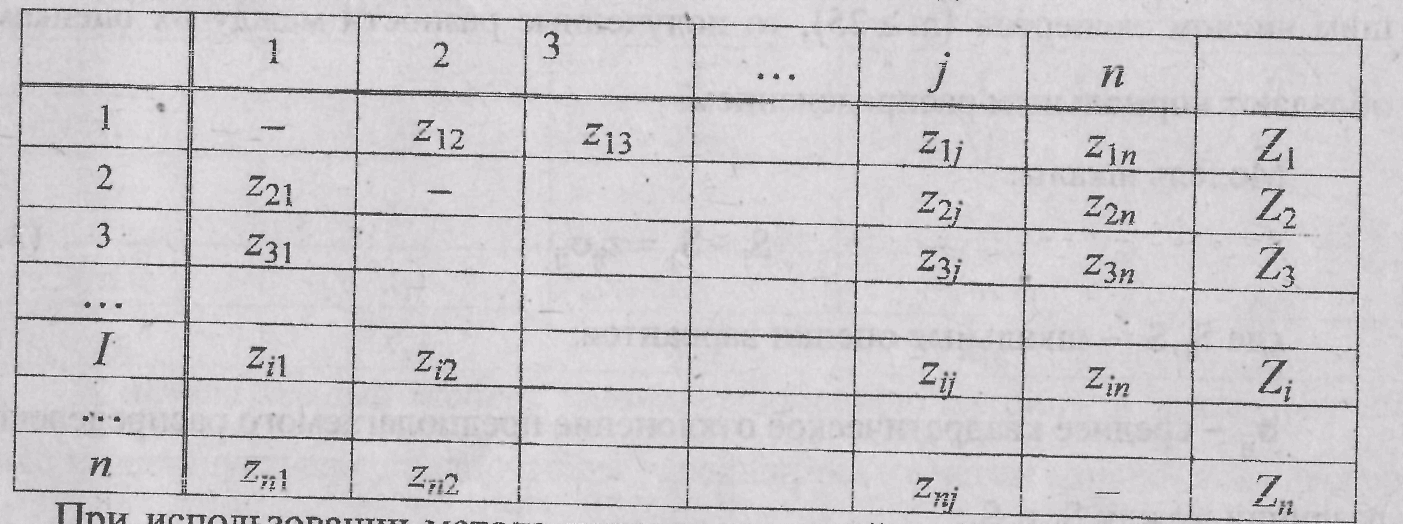
В результате сравнения, например, 5 вариантов получаем матрицу парных сравнений:

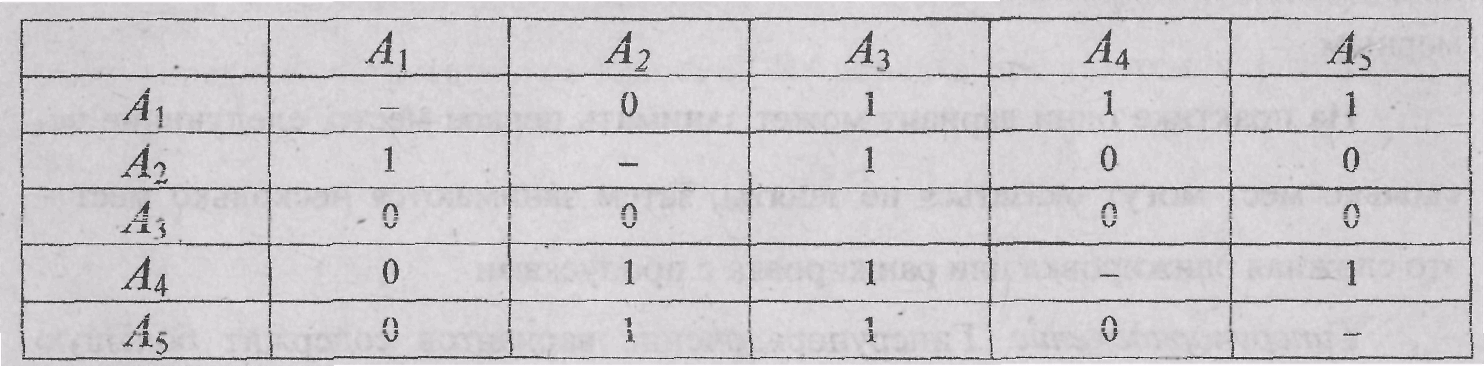
Общий вид матрицы:

Сначала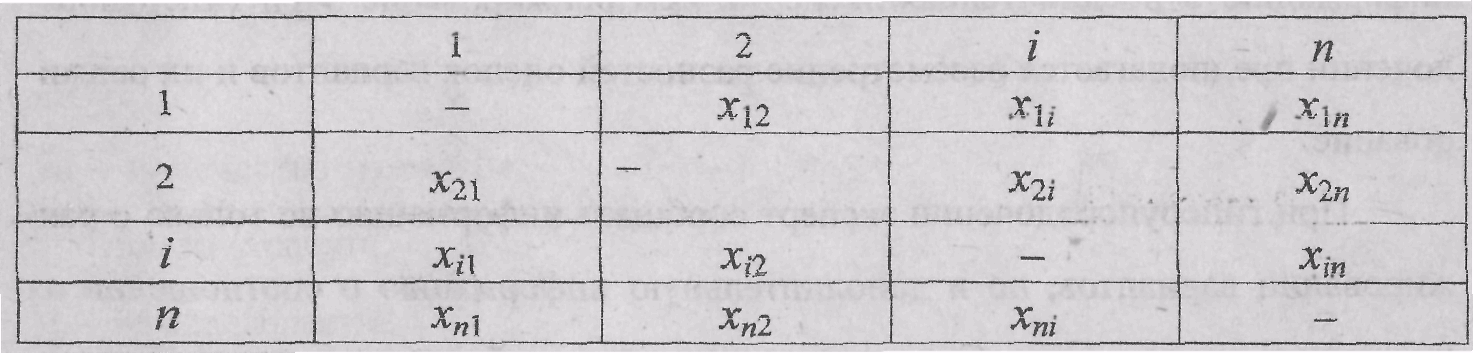 каждый эксперт заполняет подобную матрицу, а затем получен- ные индивидуальные предпочтения усредняются с учетом мнений всех экспертов. На основе этого строится вторая матрица , показывающая процентное отношение случаев, когда вариант оказывается более значимым, нежели вариант j а общем числе полученных оценок.

Элементы матрицы обладают тем свойством, что

где - число экспертов.

Матрица для случая когда вариант i предпочтительней выглядит сле- дующим образом:

26

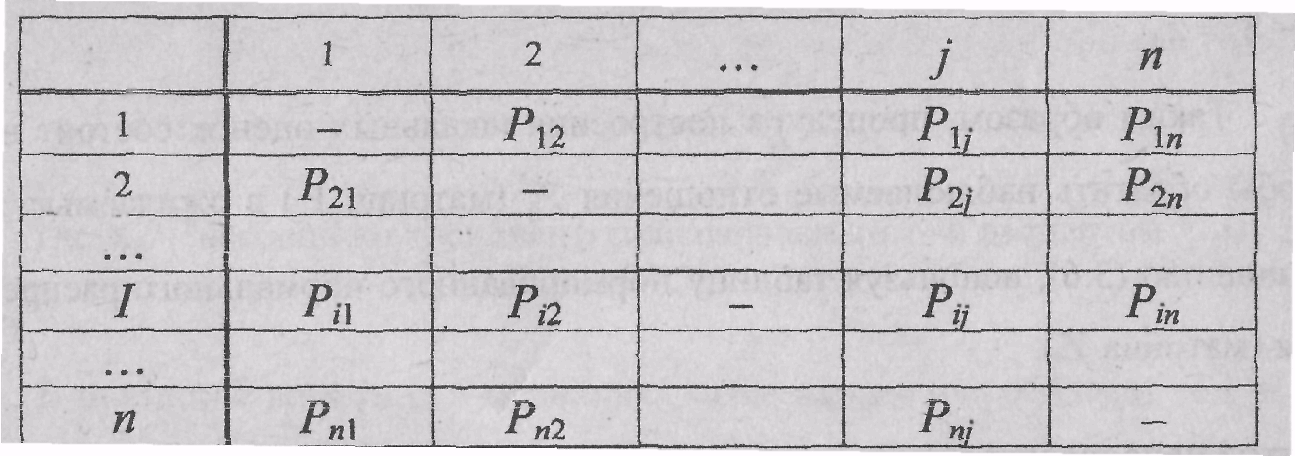
После получения обобщенной матрицы предпочтений , элементы кото рой представляют собой относительные числа предпочтений, полученных от всех экспертов, по каждому варианту перед каждым другим вариантом произ водится их шкалирование. Шкалирование основано на законе сравнительных суждений, сформулированном Л. Тер Стоуном, суть которого сводится к сле- дующему: если парное сравнение факторов выполняется относительно боль- шим числом экспертов , то полученные разности между их оценками обладают нормальным распределением.

Модель шкалы:

где - шкальные оценки вариантов;

- среднее квадратическое отклонение предполагаемого распределения различий между ;

- нормированное отклонение, соответствующее , представляющем}' долю случаев предпочтения варианта варианту, т.е.

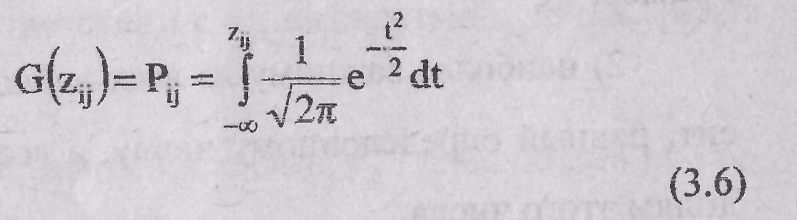
Связь между и изображена на рис. 3.1. Для упрощения принимается, что , тогда

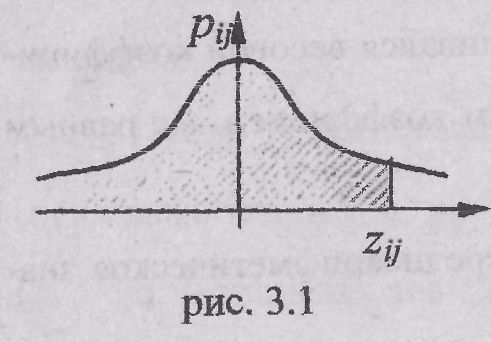
Таким образом, процедура построения шкальных оценок состоит в том, чтобы обратить наблюдаемые отношения (матрица ) в ожидаемые по

уравнению (3.6), используя таблицу нормированного нормального распределения (матрица ).

Метод непосредственной оценки

Среднее значение оценок вычисляется как:

где - число экспертов.

Матрица основного преобразования имеет вид:

метода непосредственной оценки всем вариантам на- значаются весовые коэффициенты таким образом, чтобы:

1) сумма коэффициентов была равна какому-то определенному числу (например, 1);

2) наиболее важному из всех вариантов присваивался весовой коэффициент, равный определенному числу, а всем остальным коэффициентам, равным долям этого числа.

Подобно предыдущему случаю вычисляется среднеарифметическое значение -го признака:

28

где — весовой коэффициент, присваиваемый i-м экспертом j-му при- знаку.

В принципе возможна и медианная мера, однако она обладает тем недос- татком, что результат очень чувствителен к изменению численности эксперт- ной группы, особенно когда имеются две совокупности сильно отличающихся оценок.

С

равним медианные и среднеарифметические оценки для следующих трех рядов исходных оценок, первый: второй: третий:

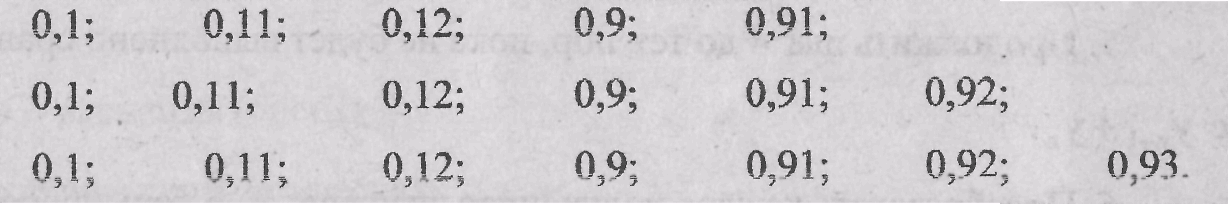
Медианное значение для первого ряда равно 0,12, для второго - 0,51, для третьего - 0,9.

Среднеарифметическая оценка для первого ряда равна 0,428, для второго - 0,51, для третьего - 0,57.

Как видно из примера, добавление каждой новой оценки сильно меняет медианную меру и гораздо слабее среднеарифметическую.