Приёмы разработки и выбора решений в условиях конфликта.
В отличие от предыдущих ситуаций, где вторым игроком была природа, здесь предполагается, что в качестве игрока выступает разумный противник.
В условиях конфликта каждый из игроков стремится к достижению своих целей (максимального выигрыша). Матрица выигрышей для двух игроков выглядит следующим образом:
.
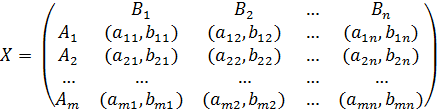В
данной матрице
и 
– это стратегии игроков
и 
соответственно, где
и
.
На пересечении каждой строки и столбца
стоит пара чисел 
,
где
– это выигрыш игрока
,
а 
– игрока
.
Дальше мы везде будем считать себя
игроком
.
При принятии решений в условиях конфликта можно различать следующие основные гипотезы.
Гипотеза 1. Каждый из игроков и не имеет информации о выборе, сделанном второй стороной. В этом случае можно принимать решение аналогично в условиях неопределённости по критерию Вальда. Тогда для игрока гарантированная оценка будет равна
,
а для игрока
.
Пусть дана матрица выигрышей для двух игроков:
.
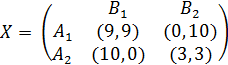Тогда
для игрока
наилучшей по этому критерию стратегией
будет
,
а для игрока
– стратегия 
.
Гипотеза
2. Предположим, что игрок
следует критерию Вальда и выбирает ту
стратегию 
,
при которой достигается оценка
.
Тогда мы должны выбрать стратегию согласно правилу
.
Гипотеза
3. Теперь мы предположим, что игрок
рассуждает точно так же, как и мы в
предыдущем случае, т. е. использует не
стратегию
,
а аналогичную стратегию 
.
Тогда мы тоже можем это учесть и выбрать
оптимально решение с учётом этой
гипотезы:
.
Рассмотрим теперь другой тип гипотез: когда один из игроков обязан сообщить о своём ходе другому игроку.
Гипотеза 4. Пусть мы знаем ход игрока , который он обязан нам сообщить. Пусть это будет стратегия . Тогда мы можем так же решить задачу максимизации и выбрать свою стратегию:
.
Гипотеза 5. Пусть теперь игрок должен знать наш ход. В этом случае он наверняка будет придерживаться той стратегии, которая будет получена аналогичным образом предыдущему случаю. Тогда при этом нам только остаётся так воздействовать на противника, чтобы он в максимальной степени соответствовал нашим целям:
,
где
- это некоторая функция, которая содержит
для каждой стратегии
значение
,
при котором
максимально.
Если
максимум 
при заданном 
достигается не в одной точке
,
а на некотором множестве 
,
то гарантированный результат будет
выглядеть следующим образом:
.
Для всех рассмотренных случаев было предположено, что оба игрока, не только точно знают свои цели, но и цели своего противника. Гораздо чаще мы не знаем точно целей второго игрока. Кроме того, необходимо учитывать и сознательную дезинформацию со стороны каждого игрока.
Заключение
В данном докладе были рассмотрены приёмы разработки и выбора решений в условиях неопределённости, риска и конфликта. Были так же рассмотрены различные критерии, по которым можно принимать решение, анализ последовательности принимаемых решений и состояний среды с помощью дерева решений, и принятие решений в условиях конфликта, когда известны точные цели своего противника.