2. Выбор решения по критерию Вальда.

Этот критерий ещё называют максиминным. Природа для этого критерия рассматривается как агрессивно настроенный противник. В этом критерии выбирается то решение, при котором достигается максимум из минимальных выигрышей для каждой стратегии:

.

Для нашей матрицы выигрышей получаем следующее:

1. для первой стратегии ;

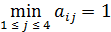2. для второй стратегии ;

3. для третьей стратегии .

Тогда наилучшим решением по данному критерию будет вторая стратегия, так как .

3. Выбор решения по критерию Сэвиджа.

Этот критерий ещё называют минимаксным. Он полностью аналогичен критерию Вальда, только здесь решение принимается на основе матрицы рисков :

.

Приведём расчёт, аналогичный предыдущему для матрицы выигрышей:

1. для первой стратегии ;

2. для второй стратегии ;

3. для третьей стратегии .

Тогда наилучшим решением по данному критерию будет первая стратегия, так как .

4. Выбор решения по критерию Гурвица.

По этому критерию выбирается та стратегия в матрице , при которой достигается следующее значение:

,

где – некий коэффициент ( , который выбирает лицо, принимающее решение.

При критерий Гурвица совпадает с максимаксным критерием, а при – с критерием Вальда.

Найдём наилучшую стратегию по этому критерию при :

1. для первой стратегии :

;

2. для второй стратегии :

;

3. для третьей стратегии :

.

Получаем, что оптимальна вторая стратегия, так как

.

Если для нахождения оптимального решения использовать матрицу рисков, критерий Гурвица имеет следующий вид:

.

В случае, когда по какому-либо критерию рекомендуется использовать одну из нескольких стратегий, выбор между ними можно сделать по какому-то дополнительному критерию. Например, по минимальному среднему квадратичному отклонению от средних выигрышей при каждой стратегии. То есть стандартного подхода по выбору критерий в условиях неопределённости нет.

3. Приёмы разработки и выбора решений в условиях риска

При принятии решений в условиях риска каждому состоянию природы соответствует вероятность. Решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска.

Если для некоторой матрицы выигрышей стратегиям природы соответствуют вероятности , то лучшей стратегией первого игрока будет та, которая обеспечивает ему максимальный средний выигрыш:

.

Если рассматривать матрицу рисков, то лучшей будет та стратегия, которая обеспечивает минимальный средний риск:

.

Пусть у матрицы выигрышей (1) и матрицы рисков (2) каждому состоянию природы соответствует одинаковая вероятность – 0.25. Тогда по критерию максимального среднего выигрыша мы получаем, что стратегия лучшая, так как

.

По критерию минимального среднего риска мы получаем ту же самую стратегию:

.

Производить расчёты лучше с той матрицей, которая определена с большей достоверностью. Это необходимо учитывать при оценках элементов этих матриц экспертами.

4. Позиционные игры

Многие задачи требуют анализа последовательности принимаемых решений и состояний среды, когда решения игрока и состояния природы порождают другие решения и состояния.

Дерево решений – это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды [2]. Оно используется, когда есть два или более последовательных множества решений и/или два или более множества состояний среды.

Рассмотрим простой пример. Руководство компании решает, создавать ли для выпуска новой продукции крупное предприятие, малое предприятие или вообще продать патент другой фирме. Размер выигрыша компании зависит от благоприятного или неблагоприятного рынка. Пусть вероятность для каждого состояния рынка будет равна 0.5.

Таблица 1

Номер стратегии	Решение компании	Выигрыш при определённом состоянии рынка (в долл.)
		Благоприятное	Неблагоприятное
1	Строительство крупного предприятия	200 000	-180 000
2	Строительство малого предприятия	100 000	-20 000
3	Продажа патента	10 000	10 000

На основе этой таблицы можно построить дерево решений (рис. 2).

1

2

3

Рис. 2. Дерево решений

Условные обозначения:

1. пустым квадратом обозначено принятие игроком решения;

2. квадратом с чёрным кругом в центре обозначено состояние природы;

3. крестиками обозначены отвергнутые решения.

Принятие решений с помощью дерева решений заключается в вычислении для каждой вершины дерева ожидаемых денежных оценок (ОДО). Вычисления проводятся при движении справа налево. После каждого вычисления остаются те ветви, которым соответствует максимальное значение ОДО, а неперспективные ветви отбрасываются.

Ожидаемая денежная оценка – это средний выигрыш в игре.

Определим ОДО для нашего примера:

1. для вершины 1: ;

2. для вершины 2: ;

3. для вершины 3: .

Так как больше остальных, то целесообразно строить малое предприятие, а остальные стратегии отбросить.

Равновероятные состояния природы на практике зачастую означают, что настоящие вероятности игроку неизвестны, и он всего лишь принимают такую гипотезу.

Рассмотрим теперь усложнённый выше пример. Пусть перед принятием решения о строительстве какого-либо предприятия или продаже патента, руководство компании должно определить, заказывать ли дополнительное обследование состояния рынка или нет. Такая предоставленная услуга обойдётся компании в 10 000 долл.. Дополнительное исследование изменит значения вероятностей благоприятного или неблагоприятного состояний рынка.

Пусть, когда фирма, которая должна выполнить заказ, утверждает, что рынок благоприятный, то с вероятностью 0.78 этот прогноз оправдается, а с 0.22 – нет. Прогноз о неблагоприятном состоянии рынка оправдывается с вероятностью 0.73.

Так же предположим, что фирма, которой заказали прогноз состояния рынка, с вероятностью 0.45 скажет, что рынок будет благоприятный, следовательно, с вероятностью 0.55 она скажет, что ситуация будет неблагоприятной. Условные вероятности благоприятного и неблагоприятного рынка представлены в таблице 2.

Таблица 2

Прогноз фирмы	Фактически
	Благоприятный	Неблагоприятный
Благоприятный (0.45)	0.78	0.22
Неблагоприятный (0.55)	0.27	0.73

На основании дополнительных сведений построим дерево решений (рис. 3).

Проанализировав полученное дерево решений можно сделать вывод о том, что целесообразно заказать дополнительное обследование рынка. ОДО при такой стратегии равна 49 200 долл.. Если прогноз будет благоприятный, то выгодней строить большое предприятие, так как у него ОДО равна 116 400 долл.. Если же прогноз неблагоприятный, то лучше строить малое предприятие, у которого ОДО равна 12 400 долл..

Рис. 3. Дерево решений при дополнительном обследовании рынка