Механическая выборка
Механическая выборка заключается в отборе единиц из генеральной совокупности через равные промежутки из определенного расположения их в генеральной совокупности (по алфавиту, в пространстве, последовательности появления во времени).
При организации механического отбора возникают две задачи:
1) определение «шага отчета» (расстояния между отбираемыми единицами);
2) выбор единицы, с которой надо начинать отчет.
«Шаг
отчета» определяется путем деления
численности генеральной совокупности
на численность выборочной совокупности:
.
Для оценки средней ошибки механической выборки применяются формулы случайной бесповторной выборки:
Пример 9: Для определения скорости расчетов с кредиторами в порядке механической выборки отобрали 50 платежных документов, по которым средний срок перечисления денег оказался равен 28,2 дня, со среднеквадратическим отклонением 5,4 дня. Определить средний срок всех платежей в течение данного года с вероятностью 0,95.
Решение.
Комбинированная выборка
Средняя ошибка комбинированной выборки определяется по формулам (условные обозначения даны раньше):
при
повторном отборе:
;
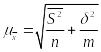при
бесповторном отборе:
.
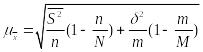Многоступенчатая выбрка
Число ступеней отбора может быть и более двух. Если число ступеней отбора больше двух, то средняя ошибка выборки определяется по формуле
,
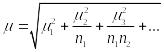где
,
,
– средние ошибки выборки на отдельных
ступенях отбора;
,
– численность выборок на соответствующих
ступенях.
Малые выборки
Выборки, при которых наблюдением охватывается небольшое число единиц (n < 30), принято называть малыми выборками. Они обычно применяются в том случае, когда невозможно или нецелесообразно использовать большую выборку (например, исследование качества продукции, если это связано с ее разрушением, в частности на прочность, на продолжительность срока службы и т.д.).
Предельная ошибка малой выборки определяется по формуле:
где t – коэффициент доверия малой выборки, зависящий не только от заданной доверительной вероятности, но и от численности единиц выборки.
Средняя (стандартная) ошибка малой выборки:
,
где S2 – дисперсия малой выборки.
S²
=
где
–
среднее значение признака по выборке;
п – 1 – число степеней свободы.