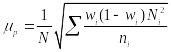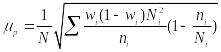Типическая (районированная) выборка

Распределение единиц выборочной совокупности между группами:

1.пропорционально численности групп в составе генеральной совокупности. Такой отбор называется пропорциональным.

N – общая численность единиц в генеральной совокупности:

N = + N₂ + ... + N_k,

где , N₂ , …,N_k – численность отдельных групп генеральной совокупности.

Объем выборки для каждой группы:

где n – общий объем выборочной совокупности.

– удельный вес данной (i-й) группы в генеральной совокупности;

п = + п₂ + ... + п_к .

2. способом оптимального размещения, при котором число наблюдений в группе определяется по формуле:

Таблица 2

Формулы ошибок типической выборки

Средняя ошибка (µ)	Способ отбора единиц
	повторный	бесповторный
Для средней: а) при пропорциональном размещении единиц б) при оптимальном размещении единиц
Для доли: а) при пропорциональном размещении единиц б) при оптимальном размещении единиц

– средняя из групповых выборочных дисперсий:

– внутригрупповая дисперсия данной (i-й) группы в выборочной совокупности;

– средняя из групповых выборочных дисперсий доли:

.

Пример 6: В целях изучения доходов населения по трем районам области сформирована 2%-ная выборка, пропорциональная численности населения этих районов.

Район	Численность населения, чел.	Обследовано, чел.	Средний доход на 1 человека, тыс. руб.	Дисперсия
1	120 000	2400	8,9	1,3
2	170 000	3400	8,5	1,1
3	90 000	1800	8,7	1,6

Определите границы среднедушевых доходов населения по области в целом при уровне вероятности 0,997.

Решение:

Серийная выборка

Сущность серийной выборки заключается в том, что вместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение. На практике чаще всего применяется серийный отбор с равными сериями.

Таблица 3

Формулы ошибок серийной выборки

Средняя ошибка (µ)	Способ отбора серий
	повторный	бесповторный
Для средней
Для доли

– межгрупповая выборочная дисперсия

=

— межгрупповая выборочная дисперсия доли:

,

где – доля единиц, обладающих данным признаком в серии;

w – доля единиц, обладающих данным признаком во всей выборочной совокупности.

Пример 7: В целях контроля качества комплектующих из партии изделий, упакованных в 50 ящиков по 20 изделий в каждом, была произведена 10%-ная серийная выборка. По попавшим в выборку ящикам среднее отклонение параметров изделия от нормы соответственно составило 9, 11, 12, 8 и 14 мм. С вероятностью 0,954 определите среднее отклонение параметров по всей партии в целом.

Пример 8: Генеральная совокупность состоит из 5000 ламп, разбитых на 50 равных по величине серий (в каждой по 100 ламп). Для проверки длительности горения ламп бесповторно отобрано 10 серий. Результаты выборки представлены в таблице:

Номера серий	1	2	3	4	5	6	7	8	9	10
Среднее число суток горения	51	54	60	61	62	70	73	77	79	92

Определить среднюю ошибку серийной бесповторной выборки.

Решение: