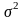Раздаточный материал к лекции «Выборочные наблюдения»

Основные этапы организации выборочного наблюдения

Определение цели, задач и составление программы наблюдения

Анализ информационных источников, используемых для выделения генеральной совокупности объектов наблюдения

Формирование генеральной совокупности для проведения выборочного обследования

Разработка методологии формирования выборочной совокупности, включающей:

- выбор способов отбора;

- определение необходимого объема выборки;

- определение этапов отбора единиц из генеральной совокупности;

- планирование и проведение пробной выборки

Формирование выборочной совокупности

Сбор данных на основе разработанной программы

Анализ полученных результатов и расчет основных характеристик выборочной совокупности

Расчет ошибок выборки и распространение ее результатов на генеральную совокупность

Параметрами генеральной совокупности называются числовые характеристики генеральной совокупности (средняя, доля, дисперсия и т.д.)

Ошибки выборки

Ошибки регистрации:

- несовершенство измерительных приборов;

- недостаточная квалификация наблюдателя;

- недостаточная точность подсчетов.

Ошибки репрезентативности

- систематические

- случайные

Степень точности оценки обычно характеризуется ее дисперсией, коэффициентом вариации, средней ошибкой и доверительным интервалом.

Точность какой-либо оценки, полученной по выборке, зависит от двух факторов:

1.

2.

Различают среднюю (стандартную) и предельную ошибки выборки.

Средняя ошибка –

Предельная ошибка –

Виды выборочных наблюдений

по способу организации:

-собственно случайная или простая,

-расслоенная (типическая или районированная),

-серийная,

-механическая,

-комбинированная,

-ступенчатая,

-многофазная.

по степени охвата единиц:

-большая

-малая выборки

Используемые обозначения

показатель	Для генеральной совокупности	Для выборочной совокупности
Объем совокупности	N	n
Среднее значение признака в совокупности
Доля единиц, обладающих данным признаком в совокупности	р	w
Дисперсия признака в совокупности
среднее квадратическое отклонение признака в совокупности

Неравенство П.Л. Чебышева: при неограниченном увеличении числа независимых наблюдений ( )в генеральной совокупности с ограниченной дисперсией с вероятностью, сколь угодно близкой к единице, можно ожидать, что отклонение выборочной средней от генеральной средней будет сколь угодно мало, т.е.

где Р – вероятность неравенства, стоящего в скобках;

-любое, сколь угодно малое положительное число;

- выборочная средняя;

- генеральная средняя;

Центральная предельная теорема А.М. Ляпунова:

где F(t) –представляет собой нормированную функцию Лапласа;

 - есть средняя квадратическая ошибка выборки.

Средняя (стандартная) ошибка выборки:

- для средней величины:

- для доли:

Средняя (стандартная) ошибка выборки зависит от:

1.

2.

Предельная ошибка выборки:

т.е. предельная ошибка выборки равна t кратному числу средних ошибок выборки.

Наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения t для выборок достаточно большого объема (n30).

t	1,00	1,96	2,00	2,58	3,00
F(t)	0,6827	0,9500	0,9545	0,9901	0,9973

Доверительные интервалы – пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра.

Для среднего значения в генеральной совокупности:

Нижняя граница будет равна:

Верхняя граница будет равна:

_{Для доли в генеральной совокупности:}

Формулы предельной ошибки позволяют решать задачи трех видов:

1. Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки.

2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более чем на определенную заданную величину. Доверительная вероятность является функцией от t, определяемой по формуле:

t=

По величине t определяется доверительная вероятность (используется Приложение).

3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.

Точность оценки параметров генеральной совокупности будет зависеть от:

1)

2)

При любом виде выборки отбор единиц производят тремя способами:

- случайный отбор (жеребьевка, таблицы случайных чисел);

- отбор единиц по какой-либо схеме;

- сочетание первого и второго способов.

В зависимости от способа отбора единиц различают:

1)

2)