2.Формулы Тейлора и Маклорена

Среди всех функций, которые нам приходилось исследовать, наиболее удобны многочлены: они определены при всех действительных , непрерывны, имеют производные всех порядков, которые также непрерывны. Поэтому более громоздкие или сложные для исследования функции выражают через степенные функции (многочлены).

36. (формула Тейлора). Если функция непрерывна и имеет непрерывные производные до порядка включительно на отрезке , причем в каждой внутренней точке этого отрезка существует производная , то на этом отрезке представима в виде: , где .

Следствие. (формула Маклорена). При имеем , где .

Доказательство формулы Тейлора во многом повторяет рассуждения, которые были приведены при доказательстве формулы бинома Ньютона (п. 70). Строгое доказательство можно найти в учебниках по математическому анализу для университетов.

Покажем, как получить соответствующие формулы для некоторых элементарных функций.

102. Для функций и при выполнены условия теоремы 48, поэтому , где ; , где .

Действительно, с учетом того, что функция – нечётная, искомое разложение можно искать в виде: . (1)

Чтобы найти , продифференцируем (1) по : (2)

Положим , получим . Продифференцируем (2) еще раз: (3)

Сравнивая (1) и (3), получим систему соотношений для коэффициентов : ; ;… ; .

Так как , последовательно находим: ; и так далее. Подставляя полученные значения для в формулу (1), имеем: .

По формуле (2) находим разложение для ;

8. для функции справедливо разложение: , где .

102. Многочлен разложить по целым положительным степеням бинома .

24. ; ; ; при . Вычислим ; ; ; , тогда по формуле Тейлора получим: .

Итак, .

3.Приближенное решение уравнений методом хорд и касательных

Многие задачи математики сводятся к отысканию корней уравнения . Но для большинства функций не существует формул для отыскания корней, а если формулы и существуют, то часто настолько громоздки, что корни приходится вычислять приближенно. Самым простым численным методом решения уравнения вида является метод половинного деления, упоминаемый в п. 48 при доказательстве теоремы Больцано-Вейерштрасса.

Пусть функция непрерывна и монотонна на отрезке , а её значения на концах этого отрезка имеют разные знаки, тогда на отрезке лежит один и только один корень уравнения . Справедливость этого утверждения следует из теоремы Вейерштрасса и условия монотонности функции .

Рассмотрим еще два способа численного решения уравнений: 1) метод хорд; 2) метод касательных.

Суть метода хорд состоит в том, что вместо значения - точки пересечения с осью абсцисс графика функции , находят точку пересечения с осью абсцисс хорды, соединяющей точки и (рисунок 59).

Уравнение хорды : . Положим и найдем : . Будем считать полученное значение первым приближением и обозначим . Итак, . (1)

Чтобы получить второе приближение, нужно вычислить и в зависимости от знака рассмотреть либо отрезок , либо отрезок . Для ситуации, изображенной на рис. 59, таким отрезком является отрезок . Повторив вычисления, с помощью которых была получена формула (1), мы получим . (2)

Продолжая процесс построения хорд, получим рекуррентную формулу: . (3)

Вычисления производятся до тех пор, пока разность между двумя последовательными приближениями станет не больше заданной границы точности: , где - заданная граница точности; тогда .

102. Найдем методом хорд с точностью до 0,01 значение корня уравнения , расположенного на отрезке .

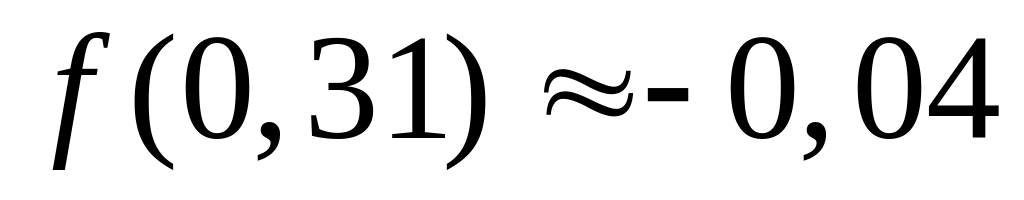25. ; и при , значит, на отрезке расположен один корень. Воспользуемся формулой (1) ; ; воспользуемся формулой (2); ; ; воспользуемся формулой (3); ; ; .

Мы видим, что , значит с точностью до 0,01 корень уравнения равен 0,32.

12. .

Если функция не только непрерывна, но и дифференцируема на отрезке , то можно заменять кривую не хордой, а касательной, проведенной в одном из концов отрезка . В этом и состоит метод касательных (метод Ньютона).

Уравнение касательной, проведенной в точке к графику функции , имеет вид: .

Чтобы найти точку пересечения касательной с осью абсцисс, положим и найдем : . (4)

Если касательную проводить в точке , то абсцисса точки пересечения вычисляется по формуле: . (5)

Д

B

ля метода касательных не все равно, в какой точке строить касательную. Рассмотрим рисунок 60: как видно, в первом случае касательную нужно строить в точке , а касательная, построенная в точке вообще не пересекает ось абсцисс на отрезке ; во втором случае – все наоборот.

Сравним знаки и со знаком второй производной функции на отрезке ; на рисунке 60(1) и ; на рисунке 60(2) и . Приходим к выводу:

Касательную надо проводить в том конце, где знак функции совпадает со знаком второй производной на отрезке (предполагается, что этот знак постоянен на отрезке ).

Найдя приближенное значение по формуле (4) или (5), надо вновь применить эту формулу к полученной точке. И в этом случае процесс продолжается до тех пор, пока последовательные значения не совпадут в пределах заданной точности. Иными словами, надо выбрать начальное приближение или и построить последовательность по рекуррентной формуле: . (6)

Процесс прерывается, когда , где - заданная точность; тогда .

102. Найдем методом касательных с точностью до 0,01 значение корня уравнения , расположенного на отрезке .

26. ; ; . На отрезке выполняется неравенство , поэтому касательную надо проводить в точке, где функция положительна, то есть . Вычислим и , и подставим в формулу (5): ; продолжим вычисления: , , получим: . Далее находим: . Поскольку , то .

Ответ: .

9. 1. Сравним рисунки 59 и 60(2), можно сделать вывод, что метод хорд и метод касательных дают различные приближения точного корня : метод хорд – с недостатком, а метод касательных с избытком; поэтому для ускорения процесса иногда применяют комбинированный метод – от отрезка переходят к отрезку , где – первое приближение методом хорд, – первое приближение методом касательных и так далее. При этом , где и соответствующие приближения. Так, для разобранных примеров 129 и 130: при получим с точностью до 0,01.

10. 2. Обратим внимание на единообразие рекуррентных формул (3) и (6) для последовательностей приближений корня уравнения : , где – угловой коэффициент. Для метода хорд он равен – угловой коэффициент хорды с концами и , а для метода касательных – – угловой коэффициент касательной к кривой в точке .

102. Решим уравнение методом касательных.

Мы имеем ; ; значит, по формуле (6) получим: . (7)

Заметим, что положительным корнем уравнения является число , поэтому мы получаем удобный алгоритм извлечения квадратного корня из положительного числа :

взять произвольное положительное число и построить последовательность приближений по формуле (7).

Перепишем формулу (7) в таком виде: ; (7.1) правая часть – среднее арифметическое чисел и , а – их среднее геометрическое; таким образом, смысл описанного процесса – на каждом шагу искомое среднее геометрическое чисел и заменяется их средним арифметическим.

Докажем, что последовательность, заданная формулой (7), сходится к , независимо от выбора :

1. по неравенству Коши , значит, для любого натурального (8) и ;

2. рассмотрим , значит, - не возрастает.

Итак, последовательность – не возрастает и ограничена снизу (8), значит, по аксиоме Больцано–Вейерштрасса, у неё есть предел. Обозначим его ; тогда перейдем к пределу в равенстве (7); получим: , откуда и . Итак, .

102. Вычислить с точностью до 0,0001.

27. выберем и воспользуемся формулой .

Тогда ;

;

.

Итак, , значит, с точностью до 0,0001.

Ответ: с точностью до 0,0001.