2.Теоремы Ролля и Лагранжа

Рассмотрим теоремы, с помощью которых можно получить достаточные условия монотонности и экстремума функции.

36. (Теорема Ролля). Если функция :

1. непрерывна при всех ;

2. дифференцируема при всех ;

3. на концах отрезка принимает равные значения: ,

то существует такая точка , в которой производная функции обращается в нуль; .

2. заметим, что если функция - постоянная ( ), то теорема справедлива для любой точки из интервала , поэтому будем доказывать теорему для функции , не являющейся постоянной. Поскольку функция непрерывна на отрезке , то она имеет на нем свое наименьшее и наибольшее значение (теорема Вейерштрасса, п.48); , . Хотя бы одно из них достигается во внутренней точке отрезка (иначе ). Пусть это будет точка . Таким образом, в точке функция имеет экстремум и дифференцируема. Тогда по теореме Ферма, в этой точке производная равна нулю: , что и требовалось доказать.

Интересен геометрический смысл теоремы Ролля. Если выполнены условия:

1. - непрерывна при ;

2. – дифференцируема при ;

3. ,

т о существует внутренняя точка такая, что касательная в этой точке к графику функции параллельна оси (смотри рисунок 46).

Следствие из теоремы Ролля: между двумя корнями дифференцируемой функции имеется, по меньшей мере, один корень производной.

36. (Теорема Лагранжа). Если функция :

1. непрерывна при всех ;

2. дифференцируема при всех , то существует такая точка , в которой .

3. введем вспомогательную функцию так, чтобы для нее выполнялись условия теоремы Ролля, действительно:

1. – непрерывна для всех , как сумма непрерывных функций при ;

2. – дифференцируема для всех : ;

3. параметр найдем из условия : .

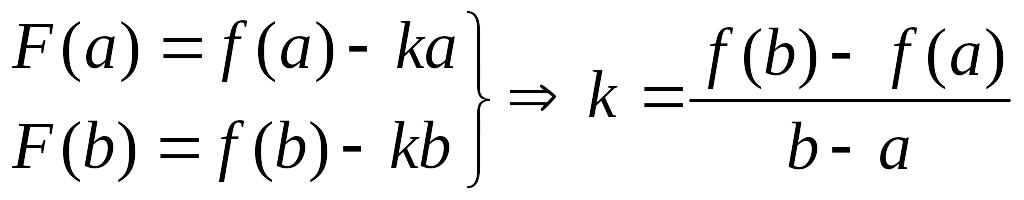Итак, функция удовлетворяет условиям теоремы Ролля, значит, существует такая точка , в которой , то есть , значит, , что и требовалось доказать.

Из равенства следует, что (1).

П оскольку – приращение аргумента на отрезке , а – приращение функции на этом отрезке, то формулу (1) называют формулой конечных приращений.

Геометрический смысл теоремы Лагранжа: если выполнены условия теоремы, то существует такая точка , касательная в которой параллельна хорде, стягивающей дугу с концами в точках и , так как - угловой коэффициент этой хорды (смотри рисунок 47).

Следствие: если функция непрерывна на отрезке и для всех , то функция постоянна на отрезке .

102. Покажем, что функция на отрезке удовлетворяет теореме Ролля, и найдем соответствующее значение .

4. функция непрерывна и дифференцируема для всех ; , значит, на отрезке теорема Ролля применима для данной функции.Для нахождения составим уравнение: , значит, ; ; ; но отрезку принадлежит лишь , поэтому .

102. Проверим выполнение условий теоремы Лагранжа для функции на отрезке и найдем соответствующее значение .

5. функция непрерывна и дифференцируема для всех , поэтому теорема Лагранжа применима. Найдем ; ; составим уравнение: ; , ; . Отрезку принадлежит , значит, .