Пластична деформація

Якщо тіло виготовлене з пластичного матеріалу, його поведінка під навантаженням буде відрізнятись від поведінки пружного тіла. Спочатку, коли напруження дуже малі, пластичне тіло буде себе поводити подібно до пружного тіла. Однак, коли напруження досягають певного значення (границя текучості τ_т), деформація буде зростати без збільшення напруження. Графічне зображення закону деформації пластичного матеріалу показано на рис.3.5.

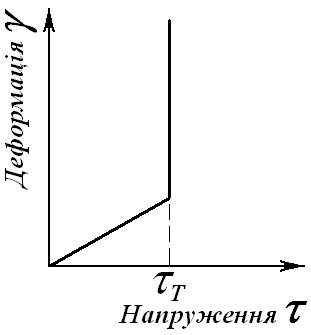
Рис.3.5. Графік деформації пластичного матеріалу

В’язкість. В’язка течія

В’язкість є мірою опору течі рідини і чисельно дорівнює відношенню напруження зсуву (τ) до швидкості зсуву :

(Закон Ньютона) (3.18.)

Рідини, що підпорядковуються цьому закону називаються ньютонівськими. Якщо деформація такої рідини здійснюється безмежно повільно, то в матеріалі, який деформується, не виникає ніяких напружень. Шари рідини зсуваються один відносно іншого без жодного опору. Розвиток деформації залежить тільки від часу дії напруження зсуву. Тому і використовують в якості критерію опору матеріалу розвиткові деформації поняття швидкості деформації ( ). Однак, як тільки швидкість зміщення шарів зростає, виникає опір зсуву. Для в’язких ньютонівських рідин ця сила опору тим більша, чим більша швидкість деформації. Рівняння, в які входить в’язкість, значно спрощуються, якщо замість неї використовувати обернену величину, яка називається текучістю (φ):

(3.19.)

В’язка течія

Рідини і гази відрізняються від твердих тіл своєю рухливістю. Під дією різниці тисків вони рухаються – течуть. Течія є одним з видів деформації при якому величина деформації γ безперервно збільшується під тиском постійно діючої сили. Рух газів відрізняється від руху рідин тим, що він супроводжується стисненням і зміною густини. Рідина в звичайних умовах не стискається, а її густина залишається практично сталою.

Якщо під дією сил деформація тіла неперервно збільшується, то це означає, що матеріал тече. Розрізняють два види течій: пластична і в’язка.

Пластична течія виникає тільки тоді, коли сила перевищує деяку межу (межу текучості). В’язка течія виникає під дією будь-яких навантаженнях, навіть при малих.

В’язка та пластична деформації виникають при напружені, але після зняття напруження не зникають на відміну від пружної деформації. Пружна деформація еквівалентна величині напруження. А при в’язкій або пластичній деформації швидкість деформації пропорційна величині діючого напруження.

Як згадувалось вище, математично закон Ньютона записується як:

Графічно закон Ньютона зображується прямою 1 (рис. 3.6.), кутовий коефіцієнт якої рівний 1/η.

Існує великий клас рідин, у яких величина швидкості зсуву зростає швидше, ніж напруження зсуву. Графічно це зображено на прикладі кривої 2. В’язкісні характеристики таких рідин неможливо охарактеризувати постійною величиною. За аналогією з ньютонівськими рідинами можливо прийняти, що в будь-якій точці кривої 2 величина швидкості зсуву також визначається законом Ньютона. Тоді коефіцієнт в’язкості втрачає значення константи, а сам, в свою чергу, залежить від швидкості (або напруження) зсуву. В цьому випадку його називають коефіцієнтом ефективної в’язкості і позначають . Рідини, в’язкість яких залежить від режиму течії називають аномально-в’язкими, а явище – аномалією в’язкості. Графіки такого типу (рис. 3.6.) одержали назву кривих течії.

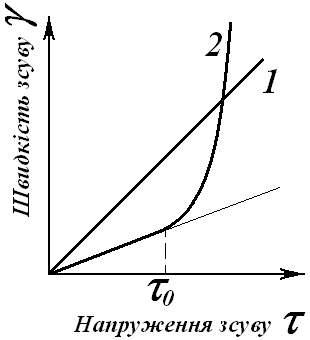
Рис.3.5. Криві течії

1 – ньютонівська рідина; 2 – аномально-в’язка рідина

Переважно усі полімери та їх розчини в умовах переробки володіють аномалією в’язкості, що значно ускладнює задачу побудови кількісних теорій процесів переробки.