Напруження
Сили, які діють на тіло поділяються на дві групи:
а) внутрішні, які зв’язані із взаємодією окремих частин тіла;
б) зовнішні, які залежать від дії оточуючих сил.
Під дією зовнішніх сил проходить зміна форми і розмірів тіла – всі реальні тіла деформуються. Якщо зовнішні сили прикладені до поверхні тіла, то, в залежності від напряму дії, вони поділяються на нормальні, направлені перпендикулярно до поверхні, і тангенціальні, які направлені по дотичній до цієї поверхні. Відношення сили до площі, на яку вони діють, носить назву напруження, яке є мірою інтенсивності внутрішніх сил. Величина і характер деформації залежить від властивостей матеріалу тіла, його форми і способу прикладення зовнішніх сил.
Розглянемо приклад появи деформації:
Рис. 3.1. Приклад деформованої призми |
Нехай в деякий
початковий момент часу
|
,
тіло мало форму паралепіпеда ABCDEKLM,
яке в момент часу
деформувалося і прийняло форму фігури
A’B’C’D’E’K’L’M’.
При цьому довжина паралепіпеда
зменшилась на
.Змінилась
також його висота та ширина.
є пропорційне
початковій довжині
та силі
,
яка спричинила деформацію і обернено
пропорційна площі поперечного січення
паралелепіпеда (∆l↑
S↓) та деякій
постійній Е,
яка характеризує матеріал з якого
виготовлене тіло:
–
закон Гука;
(3.3.)
(3.4.)
Сила, яка діє на
одиницю площі називається напруженням
і позначається
.
;
(3.5.)
–
відносне видовження.
(3.6.)
Таким чином, закон Гука встановлює залежність між напруженнями, які діють в твердих тілах, та їх видовженням, або деформацією при одноосному розтязі:
(3.7.)
У розглянутому випадку маємо одноосне навантаження, але під дією складної системи сил тіло може деформуватись по трьох напрямках (x,y,z). Причому, деформація в кожному з напрямків визначається за рахунок дії відповідних складових напружень.
Особливістю течії ньютонівських рідин є те, що в них повністю співпадають напрями дії напружень та швидкостей деформацій, а в полімерах – ні. При будь-якому виді деформації в полімерних системах виникають напруження, які діють у всіх напрямках, а саме при зсувній течії – перпендикулярно до площини та напрямку зсуву. Такі напруження називають “нормальними”.
Розглянемо течію в’язкого середовища в просторовій системі координат (наприклад розплавлений полімер під тиском). В масі середовища виберемо деякий об’єкт (наприклад у формі паралелепіпеда):
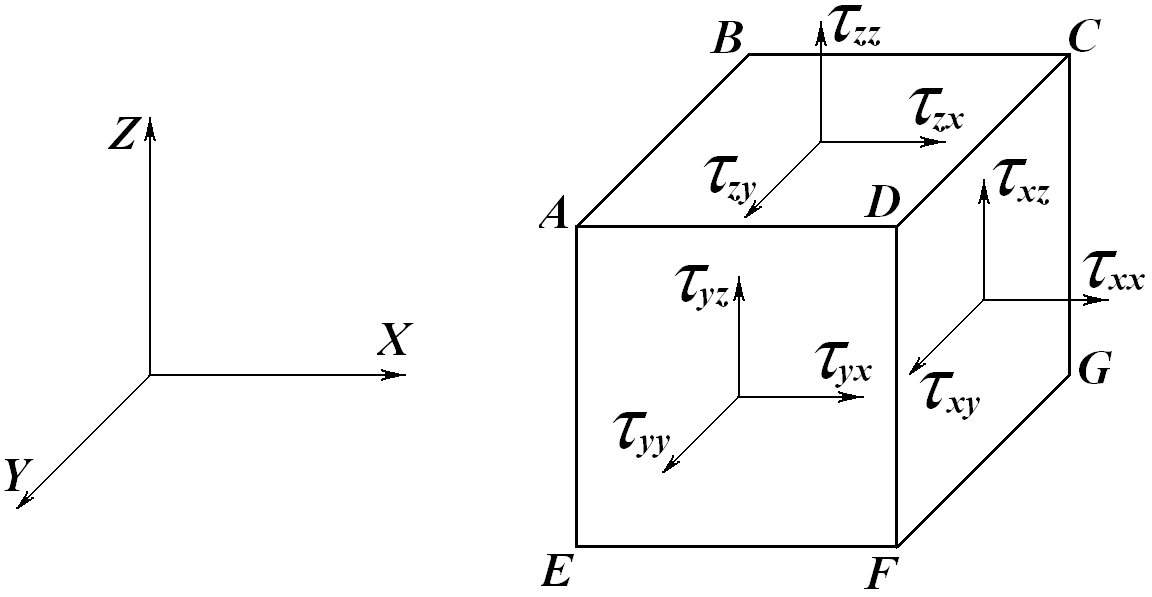
Рис. 3.2. Розподіл напружень, які діють на елементарний об’єм матеріалу
З боку оточуючого середовища на об’єкт діють деякі поверхневі сили.
Повне напруження, як будь-який вектор у тривимірному просторі може бути розкладене по осях координат, одна з яких направлена по нормалі до площини січення, а дві інші розміщені в площині січення.
Напруження
позначаємо
(літерою з двома індексами). Перший
індекс вказує в якій площині діє
напруження, що розглядається, другий –
вздовж якої осі. Наприклад, на грані
ABCD
діє три напруження
.
Так як грань паралелепіпеда розміщена
нормально (перпендикулярно) до осі z
перший індекс при напруженнях, діючих
на дій грані - z.
Одне з напружень
–нормальне, два
– дотичні. Нормальним напруженням також
є проекція вектора повного напруження
на нормаль, а проекція вектора на осі в
площині січення є дотичним напруженням.
Таким чином напружений етап середовища
обмеженого розглянутим паралепіпедом
характеризується наступними величинами
, які складають так званий тензор
напружень:
.
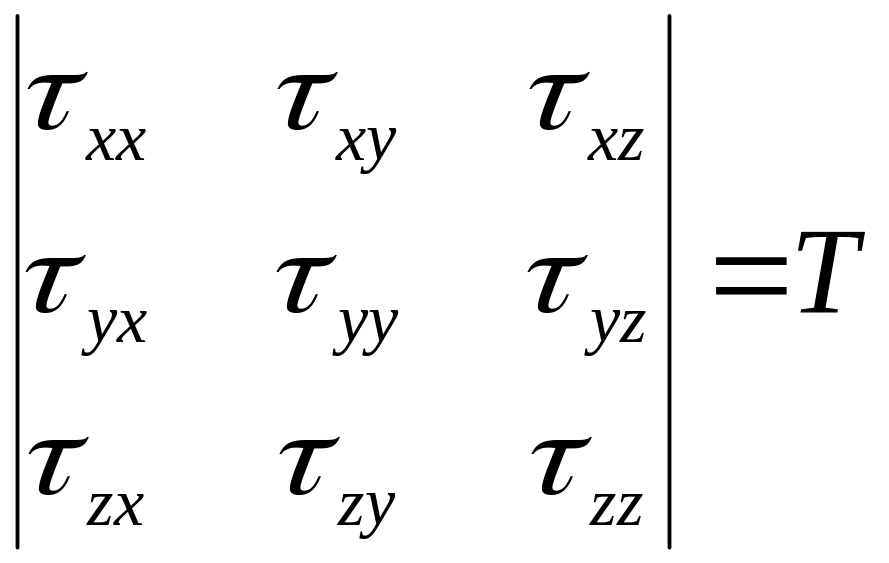(3.8.)
Дотичні напруження взаємно перпендикулярних площин рівні і направлені або до ребра, або від ребра елемента об’єму. Нормальне напруження, прикладене до всієї поверхні тіла, носить назву тиску, тому будь-яке механічне напруження вимірюється в одиницях тиску.