4. Модель Каргіна-Слонімського

Суттєвим доповненням моделі Каргіна-Слонімського є те, що всі елементи ланцюжку моделей поміщені в загальне в’язке середовище (Рис. 6.13.).

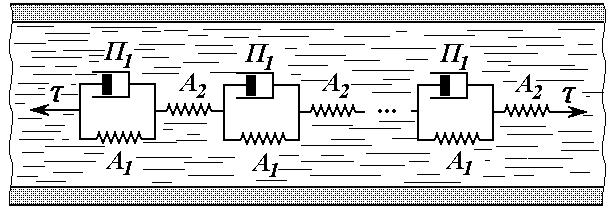
Рис. 6.13. Модель Каргіна-Слонімського

Це дає можливість моделювати лінійний полімер. Три елементи моделі , і з’єднуються так, що величини, які характеризують дані елементи моделі набувають певного фізичного значення.

Наприклад, величина, яка характеризує пружність пружини , моделює константу пружності полімера, обумовлену деформацією валентних кутів та зв’язків в ланцюгових макромолекулах.

Пружність пружини - це константа пружності, яка визначається зміною числа конформацій ланцюгових макромолекул при їх деформації внаслідок внутрішнього обертання. Поршні характеризують внутрішню рухливість макромолекул, тобто кінетику переходу від одної конформації до іншої.

В’язкість рідини, в яку поміщені моделі сегментів, характеризує їх рухливість і визначає протидію їх руху.

Модель здатна проявляти весь комплекс релаксаційних явищ в амфорних полімерах.

Лекція 7

Криві течії

План лекції

1. В’язкість.

1.1. Динамічний та кінематичний коефіцієнт в’язкості.

1.2. Визначення динамічного коефіцієнту в’язкості з кривих течії.

2. Криві течії.

2.1. Індекс течії.

2.2. Степеневий закон.

В’язкість є однією з основних характеристик рідини, яка характеризує сили внутрішнього тертя і являє собою властивість рідини чинити опір її руху під дією сил, які викликають цей рух.

або

(Закон Ньютона) ,

де τ – напруження зсуву, Н/м²;

– швидкість зсуву, сек^-1.

Характеризується в’язкість двома коефіцієнтами:

• динамічним коефіцієнтом в’язкості η ;

• кінематичним коефіцієнтом в’язкості μ, який визначається як відношення динамічного коефіцієнту до густини:

(7.1.)

Для ньютонівських рідин (як слідує із закону Ньютона): динамічний коефіцієнт в’язкості η є коефіцієнтом пропорційності між дотичним напруженням та швидкістю деформації рідини.

Рідини, які описуються законом Ньютона називають ньютонівськими, а коефіцієнт в’язкості η – ньютонівським коефіцієнтом в’язкості. Він може бути визначений за так званою кривою течії рідини – геометричному представленню рівняння закону Ньютона (Рис. 7.1.).

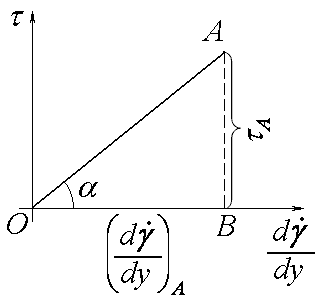
Рис. 7.1. Крива течії ньютонівської рідини

На осі ординат відкладене значення напруження , а по осі абсцис – градієнта швидкості .

З трикутника АОВ:

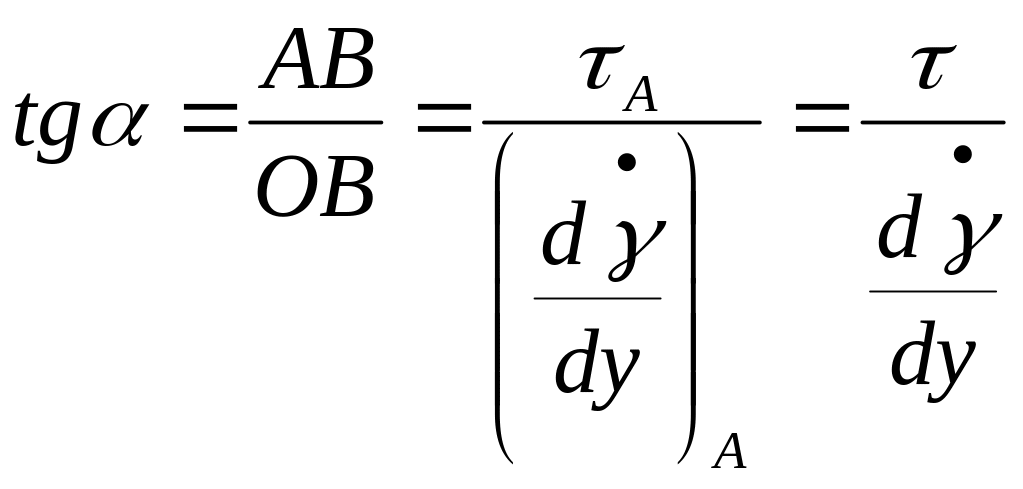. (7.2.)

Використовуючи дане рівняння та закон Ньютона, бачимо, що tgα = η, тобто динамічному коефіцієнту в’язкості.

Ньютонівський коефіцієнт в’язкості залежить тільки від та в рідині:

. (7.3.)

Закон Ньютона справедливий для більшості газів та рідин, у яких дисипація енергії визначається зіткненням невеликих молекул.

Повну залежність в більшості випадків можна представити формулою:

, (7.4.)

де А₀, С, D, В₀ - деякі константи;

x, y - параметри, характерні для даної рідини.

Якщо течія будь-якої рідини не описується законом Ньютона, то така рідина, як зазначалось вище, називається неньютонівською (аномально-в’язкою). Крива течії такої рідини не буде визначатися прямою лінією, а коефіцієнт η не буде сталою, і може залежати від градієнта швидкості і т.д.

На відміну від ньютонівських рідин, для яких в’язкість є сталою величиною, в’язкість більшості розплавів і розчинів полімерів залежить при сталій температурі від режимів формування, тобто від напруження зсуву. При переробці полімерів напруження зсуву і швидкість деформації змінюються в широких межах, оскільки для повної характеристики реологічних властивостей розплаву потрібно представляти його криву течії при зміні швидкості зсуву в діапазоні 3-4 десяткових порядків. Тому криві течії будують в подвійних логарифмічних координатах «lg - lgτ». Характер кривої течії при цьому не змінюється. Якщо величини масштабів, вибраних для осі абсцис і для осі ординат, однакові, системам, які володіють властивостями ньютонівських рідин, будуть відповідати прямі, нахилені до осей під кутом 45°. Криві течії реальних розплавів полімерів дещо вигнуті (Рис. 7.2.).

Рис. 7.2. Крива течії неньютонівської рідини

На кривій є три ділянки. При τ < τ0 має місце ньютонівська течія із сталою в’язкістю, яку називають найбільшою ньютонівською в’язкістю ηнб. На цій ділянці (І) справджується рівняння: . (7.5.) Кутовий коефіцієнт прямої: . (7.6.) Величина n характеризує ступінь аномалії в’язкості і отримала назву індексу течії. При зростанні напруження τ0 < τ < τ1 розплав полімеру проявляє аномально-в’язкі властивості. Ця ділянка (ІІ) не описується законом Ньютона. Коефіцієнт в’язкості змінюється в кожній точці кривої.

На ділянці (ІІ) необхідно вводити деяку функцію від напруження зсуву, яка характеризує фактичну нелінійність зв’язку між і τ. Такою функцією є ефективна в’язкість:

(7.6.)

Ефективну в’язкість називають іноді еквівалентною в’язкістю.

В області високих напружень (ІІІ) при τ > τ₁ має місце ньютонівська течія зі сталою в’язкістю, яка одержала назву найменшої ньютонівської в’язкості η_нм. На даній ділянці кривої течії структура полімеру повністю зруйнована, розвивається процес течії окремих макромолекул. Таким чином, існування ефективної в’язкості, яка визначає специфіку поведінки полімеру при течії, пояснюється одночасним розвитком основних видів деформації. Для структурної ділянки кривої індекс течії n є більшим 1. Практично ця величина лежить в межах 1 < n ≤ 6.

Невелика кривизна кривих течії в подвійних логарифмічних координатах є причиною широкого поширення для опису структурної ділянки течії полімерів так званого степеневого закону:

(7.7.)

де k – показник консистенції рідини.

Для ньютонівських рідин величина k характеризує в’язкість. Для аномально-в’язких рідин k є своєрідним аналогом в’язкості і носить назву коефіцієнта консистенції.

Використання степеневого закону є найбільш простим способом опису кривих течії. При цьому реологічні властивості розплаву характеризуються за допомогою двох експериментальних констант: k і n.

Степеневий закон в достатній мірі описує ті ділянки структурної вітки, де залежність від τ є лінійною. Прологарифмувавши рівняння, одержимо:

(7.8.)

Степеневий закон справедливий тільки у вузькому діапазоні кривої течії, а для більш повного її опису запропоновано ряд більш складних емпіричних формул, наприклад:

(7.9.)

де k₁ і k₂ – емпіричні константи, які визначаються при обробці експериментальних даних.

Дане рівняння дає можливість достатньо точно описати криву течії при широкій зміні швидкості зсуву.

Лекція 8.