Релаксаційний спектр

Якщо спостерігати за часовою залежністю напруження при заданій величині деформації, то спостерігається явище так званої релаксації напруження. Введемо по аналогії з пружним модулем в якості характеристики будь-якої полімерної системи релаксаційний модуль Е(t). Визначимо релаксаційний модуль як відношення миттєвого значення напруження в досліджуваному зразку до величини деформації, встановленої при дослідженні в режимі постійної деформації. Для тіла Максвела:

, (6.12.)

де Е – модуль пружності,

t – час;

t₀ – час релаксації.

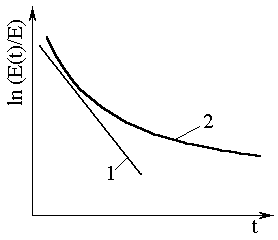
Співставлення отриманих характеристик тіла Максвела з характеристиками реальних полімерів, які знаходяться у високоеластичному або в’язко-текучому станах, показує, що між ними існує якісна залежність. Якщо взяти натуральні логарифми правої та лівої частини попереднього рівняння, то одержимо:

(6.13.)

Якщо релаксаційні властивості реального полімеру можна було б описати за допомогою тіла Максвела, то експериментальні дані по релаксації напружень в координатах – f(t) повинні були б вкластися на прямій. В дійсності ж релаксаційні властивості реальних полімерів описуються кривою:

Рис. 6.10. Криві релаксації напруження: 1 – тіло Максвела;2 – реальний полімер.

Для описання релаксаційних власти-востей реальних полімерів необхідно використовувати моделі, які складаються з набору паралельно з’єднаних елементів Максвела, кожний з яких характеризується своїм значенням модуля пружного елемента та часу релаксації. При цьому, чим більша кількість паралельно з’єднаних елементів Максвела, тим точніше буде така узагальнена модель описувати деформацій-

ні характеристики реального полімеру. Необхідність введення великої кількості паралельно з’єднаних елементів для описання деформаційних характеристик реальних полімерів є наслідком складності полімерної структури та механізму деформації реальних полімерів.

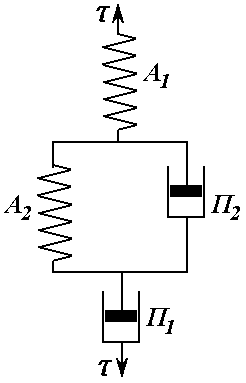
3. Об’єднана модель Максвела і Кельвіна

Рис. 6.11. Об’єднана модель Максвела і Кельвіна

Об’єднана модель Максвела і Кельвіна (рис. 6.11.) найбільш повно описує реологічні властивості полімерів, тобто закономірності їх деформацій. Вона включає в’язко-пружну поведінку як твердого, так і рідкого тіла. При прикладенні до такої моделі деякої сили миттєво відбувається деформування пружного елемента моделі на величину деформації, яка визначається модулем пружності пружини . Якщо представити цей процес графічно (Рис. 6.12.), то ця деформація буде відповідати відрізку кривої , а час – відрізку часу від початку дефор-

мування. Потім, з часом, буде відбуватись деформація в’язкого елемента і елементів і . До моменту часу пружна деформація пружини повністю закінчиться і далі буде спостерігатись в’язка течія (лінія ) до моменту часу , який відповідає моменту зняття навантажень з моделі.

Рис. 6.12. Кінетика деформації об’єднаної моделі Максвела-Кельвіна

Відрізок відповідає зменшенню пружної деформації. Він рівний по величині відрізку . Ділянка кривої відповідає загальмованому скороченню пружини , тобто зменшенню високоеластичної деформації. Дану модель можна використовувати для якісного опису реальних в’язкопружних середовищ. Така модель може бути основою для загальної моделі лінійного полімеру. Однак, вона не враховує однієї з основних особливостей полімеру – відносної незалежності окремих ділянок довгих гнучких ланцюгів макромолекул. Тому було запропоновано Каргіним та Слонімським модель наступного типу.