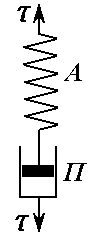- •Прийняті позначення
- •Лекція 1
- •Історичний огляд розвитку переробки пластмас
- •1.1. Методи при здійсненні яких протікають однакові фізичні перетворення (екструзія, каландрування, лиття під тиском) та обладнання для їх здійснення.
- •1. Огляд технологічних процесів та обладнання в переробці полімерів
- •2. Аналіз процесів переробки полімерів із позицій елементарних стадій
- •2) Плавлення; 3) перекачування матеріалу і створення тиску; 4) змішування;
- •5) Дегазація та розділення.
- •Основні поняття реології
- •Аксіоми реології полімерів
- •Напруження
- •Напруження зсуву
- •Швидкість зсуву
- •Накопичення та дисипація енергії
- •Деформація. Основні види деформації
- •Пружна деформація. Пружність
- •Пластична деформація
- •В’язкість. В’язка течія
- •В’язка течія
- •Види течії
- •Класифікація реологічних рідин
- •Реологічні моделі полімерних систем
- •1. Модель Кельвіна-Фойгхта
- •Релаксаційний спектр
- •4. Модель Каргіна-Слонімського
- •Криві течії
- •Вплив температури та тиску на реологічні властивості полімерів
- •1. Вплив температури на реологічні властивості полімерів.
- •2. Вплив тиску на в’язкість полімерів.
- •В’язкість полімерів. Методи визначення в’язкості
- •2. Методи визначення в’язкості.
- •3. Реологічні випробування термопластів
- •Віскозиметрія полімерів
- •Капілярна віскозиметрія
Реологічні моделі полімерних систем
План лекції
1. Ідеальні тіла.
1.1.Ідеально-пружне тіло Гука.
1.2. Ідеально-пластичне тіло.
1.3. Ідеально-в’язка рідина Ньютона.
2. Складні моделі.
2.1. Модель Кельвіна-Фойгхта.
2.2. Пружно-в’язке релаксуюче тіло Максвела. Релаксаційний спектр.
2.3. Об’єднана модель Максвела і Кельвіна.
2.4. Модель Каргіна-Слонімського.
Для точного математичного опису реологічної поведінки рідини необхідно врахувати всі фактори, які впливають на її реологічні властивості.
Реологічне рівняння для реальних рідин розв’язати дуже важко. Якісну картину течії такого середовища можна одержати на основі механічних ( або електронних) моделей або аналогій, які з певною точністю відтворюють реологічні властивості рідини. Дані моделі переважно представляють собою систему, яка складається з пружин та поршнів, і моделює такі властивості рідини, як текучість, пружність, еластичність і т. д.
І. Ідеальні тіла.
До них відносять – ідеально-пружне тіло Гука, ідеально-пластичне тіло Сен-Венана, ідеально-в’язка рідина (Ньютонівська рідина)
1) Ідеально-пружне тіло Гука.
Самою простою механічною моделлю ідеально пружного тіла є звичайна спіральна пружина (рис. 6.1. а), яка підпорядковується закону:
Якщо реальне тіло в якомусь діапазоні невеликих напружень після їх зняття раптово повертається до своєї початкової форми, то воно проявляє властивості ідеально-пружного тіла.
2) Ідеально-в’язка рідина Ньютона
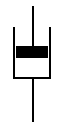
Моделлю рідини Ньютона є перфорований поршень (рис. 6.1. б), який розміщений в циліндрі з в’язкою рідиною. Дана модель характеризується тим, що між силою, яка прикладена до поршня і швидкістю його переміщення спостерігається наступна залежність:
![]() .
.
η – коефіцієнт ньютонівської в’язкості.
Рис. 6.1. Модель пружного тіла Гука (а) та ньютонівської рідини (б) |
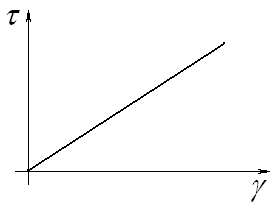
Рис. 6.2. Залежність γ від τ ідеально-в’язкої рідини |
В’язка рідина є дисипативною системою. В таких системах механічна енергія, затрачена на перемагання внутрішнього тертя і на пластичну деформацію, перетворюється в теплоту. Пружне тіло є консервативною системою – вся енергія, затрачена на деформацію, накопичується і може бути вивільнена при знятті навантаження.
ІІ. Складні моделі
Для моделювання реальних полімерних систем, яким притаманні всі реологічні властивості, використовують моделі, складені з ідеально-пружного тіла Гука та ідеально-в’язкої рідини Ньютона. Моделі ідеальних тіл можуть з’єднуватись одна з одною або послідовно, або паралельно.
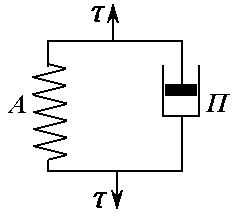
1. Модель Кельвіна-Фойгхта
Модель
Кельвіна-Фойгхта (рис. 6.3.) є деяким
аналогом ідеалізованого в’язкопружного
тіла. Вона складається з пружини
![]() та поршня
та поршня
![]() ,
які знаходяться у взаємодії. Дає
можливість моделювати явища «пружної
післядії». Під цим терміном в реології
розуміють зміну пружної деформації в
часі, коли вона поступово наростає до
деякої межі після прикладення навантаження,
або поступово зменшується після його
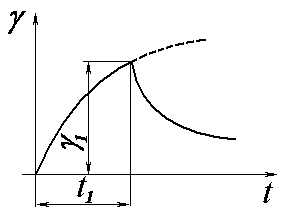
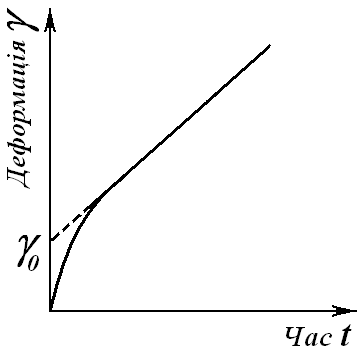
зняття (рис. 6.4.).
,
які знаходяться у взаємодії. Дає
можливість моделювати явища «пружної
післядії». Під цим терміном в реології
розуміють зміну пружної деформації в
часі, коли вона поступово наростає до
деякої межі після прикладення навантаження,
або поступово зменшується після його
зняття (рис. 6.4.).
Рис. 6.3. Модель Кельвіна-Фойгхта |
Рис. 6.4. Кінетика деформації тіла Кельвіна-Фойгхта |
Паралельне з’єднання двох елементів дає можливість записати для рівнодійної прикладених сил наступне рівняння:
![]() ,
(6.1.)
,
(6.1.)
де ![]() характеризує напруження на пружному
елементі моделі (пружині),
характеризує напруження на пружному
елементі моделі (пружині),
![]() - на в’язкому
(поршень з циліндром). Так, згідно закону
Гука
- на в’язкому
(поршень з циліндром). Так, згідно закону
Гука
![]() ,
а за законом Ньютона
,
а за законом Ньютона
![]() ,
,
де
![]() - в’язкість, тоді можна записати:
- в’язкість, тоді можна записати:
![]() .
(6.2.)
.
(6.2.)
Врахувавши час
релаксації
![]() та проінтегрувавши рівняння (6.2.),
одержимо:
та проінтегрувавши рівняння (6.2.),
одержимо:
![]() (6.3.)
(6.3.)
Рівняння (6.2.) і (6.3.) показують як залежить від часу дії напруження, тобто характер деформації моделі Кельвіна-Фойгхта.
Перемноживши всі
члени рівняння (6.3.) на
![]() ,
одержимо:
,
одержимо:
![]() .
(6.4.)
.
(6.4.)
При t<<t0, величина γ t/t0 буде дуже малою і дана модель характеризує течію, яка описується формулою Ньютона:
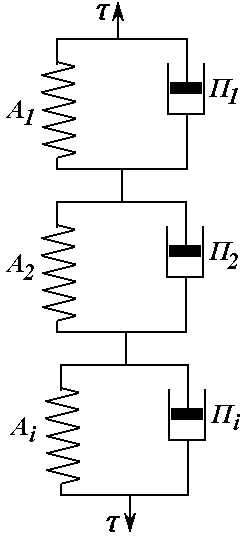
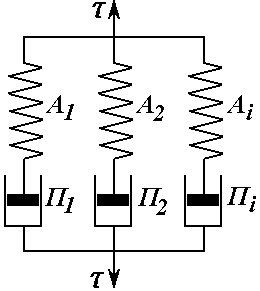
Рис. 6.5. Узагальнена модель Кельвіна-Фойгхта |
При
Використовуючи дану модель або узагальнену модель Кельвіна-Фойгхта (рис.6.5.) досліджувати безмежну та необоротню течію в’язкої рідини неможливо. Моделі дають можливість тільки моделювати поведінку в’язкопружного „твердого” тіла. |
2. Пружно-в’язке релаксуюче тіло Максвела
Рис. 6.6. Модель тіла Максвела |
Модель Максвела представляє собою з’єднані послідовно пружину та поршень (Рис.6.6). Дана модель, як і модель Кельвіна-Фойгхта, відтворює поведінку в’язкопружного середовища при його деформації. Якщо тіло Максвела деформувати, приклавши до нього постійне навантаження, то спочатку воно скачкоподібно деформується на величину, яка відповідає стисненню пружного елемента, а потім буде деформуватись з постійною швидкістю, яка відповідає величині прикладеного зусилля (Рис. 6.7.). |
З іншого боку, якщо швидко деформувати тіло Максвела, а потім зафіксувати одержану деформацію і спостерігати за зміною сили (або напруження) в часі, то початкове напруження, яке відповідає наданій величині деформації пружини, буде постійно зменшуватись за рахунок зміщення поршня. При цьому величина напруження буде змінюватись так, як зображено на рис. 6.8.
Таким чином, на прикладі тіла Максвела змодельовано явище релаксації напружень – явище постійного зменшення в часі існуючих у деформованому зразку полімерного матеріалу напружень.
Рис. 6.7. Діаграма процесу деформації тіла Максвела під дією постійного навантаження |
Рис. 6.8. Релаксація напружень в тілі Максвела |
Як видно з рис. 6.6., сумарна деформація при дії напруження , в цьому випадку буде рівна:
![]() ,
(6.5.)
,
(6.5.)
де ![]() - пружна деформація пружини;
- пружна деформація пружини;
![]() - необоротня
деформація в’язкого елемента.
- необоротня
деформація в’язкого елемента.
Використавши закони Гука та Ньютона для визначення , можна записати:
![]() .
(6.6)
.
(6.6)
Продиференціювавши
та враховуючи, що
![]() ,
одержимо:
,
одержимо:
![]() .
(6.7.)
.
(6.7.)
З рівняння (6.7.) можна одержати вираз для :
![]() ,
(6.8.)
,
(6.8.)
де ![]() - напруження в початковий момент часу
- напруження в початковий момент часу
![]() ;
;
- час релаксації.
В умовах постійної деформації для тіла Максвела рівняння (6.7.) набуває наступного вигляду:
![]() .
(6.9.)
.
(6.9.)
Інтегруючи дане рівняння за умови р = р0 при t = 0, одержимо наступну експоненційну залежність:
![]() (6.10.)
(6.10.)
Фізичний зміст часу релаксації полягає в тому, що через час t = t0 величина початкового напруження зменшується в е разів.
В тому випадку, коли на тіло Максвела діє постійне навантаження τ = const, рівняння (6.7.) перетворюється на закон Ньютона.
Аналізуючи модель Максвела, можна показати, що ця модель дає можливість описати в’язкопружну поведінку вже не „твердого”, а „рідкого” тіла.
Рис. 6.9. Узагальнена модель Максвела |
Аналогічні результати одержуються і для узагальненої моделі Максвела (Рис. 6.9.). В цьому випадку повне напруження , як функція від часу , визначається сумою напружень кожного з елементів моделей:
де
|

 б)
б)