Класифікація реологічних рідин

План лекції

1. Класифікація реологічних рідин.

1.1. Ньютонівські рідини.

1.2. Неньютонівські рідини.

1.2.1. Стаціонарні неньютонівські рідини.

1.2.1.1. Бінгамівські пластичні рідини.

1.2.1.1. Псевдопластичні рідини

1.2.1.1. Дилатантні рідини

1.2.2. Нестаціонарні неньютонівські рідини.

1.2.2.1. Тіксотропні рідини (істинно-тіксотропні, квазітіксотропні, антитіксотропні середовища

1.2.2.2. Реопектичні рідини.

1.2.3. В’язкопружні рідини.

Всі рідини поділяють на:

1. Ньютонівські рідини.

2. Неньютонівські рідини.

Ньютонівські рідини – рідини, які підлягають закону Ньютона, в яких в’язкість є постійною величиною і не залежить від швидкості зсуву. Ньютонівські рідини деформуються під впливом самих малих навантажень. Неньютонівські рідини – рідини, в’язкість яких при заданій температурі і навантаженню залежить від швидкості деформації.

Неньютонівські рідини рідини поділяються на три групи:

1. Стаціонарні неньютонівські рідини – системи, для яких швидкість деформації в кожній точці кривої течії являє собою деяку функцію тільки напруження зсуву в цій точці.

2. Нестаціонарні неньютонівські рідини – системи, які характеризуються залежністю величини швидкості зсуву від часу дії напруження.

3. В’язкопружні рідини – системи, які мають властивості як твердого тіла, так і рідини , а також частково проявляють пружне відновлення форми після зняття напруження.

Стаціонарні неньютонівські рідини описуються реологічним рівнянням:

(5.1.)

Рис. 5.1. Криві течії 1 – ньютонівські рідини; 2 – дилатантні рідини; 3 – псевдопластичні рідини; 4 – бінгамівські пластики; 5 – в’язкопластичні рідини.

В залежності від виду кривої течії (рис. 5.1.) їх можна розділити на три групи. До першої групи (криві 2, 3) належать в’язкі рідини, в яких швидкість зсуву залежить тільки від прикладених напружень. Це, так звані, дилатантні (крива 2) та псевдопластичні рідини (крива 3). До другої групи відносяться рідкі середовища, які при напруженнях , менших граничного напруження зсуву , поводять себе як тверді тіла, а при - як рідини. Це, так звані, бінгамівські пластики (крива 4). До третьої групи відносяться в’язкопластичні рідини (крива 5), яким притаманні деякі властивості рідин як першої так і другої групи

Дилатантні рідини – характеризуються тим, що при збільшенні напруження зсуву відбувається зростання ефективної в’язкості системи. Вони, так як і псевдопластики не мають границі текучості, але їх реологічна поведінка протилежна псевдопластичним рідинам, їх ефективна в’язкість поступово збільшується із зростанням швидкості зсуву. Дилатансія – зміна об’єму, викликана простим зсувом. Дилатансія може бути пружною, пластичною та в’язкою. Пластична дилатансія спостерігається в піщаних ґрунтах, суспензіях полімерів, пластизолях, наповнених розплавах полікапроаміду.

Псевдопластичні рідини (псевдопластики). Характерною особливістю їх є зниження ефективної в’язкості з ростом швидкості зсуву. Такими псевдопластиками є розчини полімерів.

Бінгамівські пластичні рідини (бінгамівські пластики), течія яких починається тільки після досягнення границі текучості, являють собою желеподібні утворення з просторовою структурою. Для того, щоб рідина текла (пластична деформація) необхідно зруйнувати цю структуру, що досягається при τ > τ_Т. Як тільки напруження стає меншим границі текучості, структура знову відновлюється. До числа бінгамівських пластиків відносяться фарби, пігменти, деякі реакційно-здатні олігомери, мінеральні наповнювачі.

До нестаціонарних рідин відносяться:

– тіксотропні рідини;

– реопектичні рідини.

Тіксотропні середовища характеризуються зменшенням в’язкості протягом часу. Для багатьох реальних матеріалів залежність між напруженням зсуву та швидкістю зсуву має часовий характер, тобто ефективна в’язкість визначається не тільки швидкістю зсуву, але й тривалістю деформації зсуву. У зв’язку з цим, зменшується або зростає з часом напруження зсуву, якщо матеріал деформується з постійною швидкістю зсуву. Розрізняють матеріали тіксотропні та антитіксотропні.

Тіксотропія – це зворотня зміна реологічних властивостей матеріалу в часі, яка виникає в результаті зовнішньої механічної дії.

Розрізняють два типи тіксотропних систем:

• істинно-тіксотропні системи, реологічні властивості яких відрізняються наявністю явно вираженої межі зсувної міцності. До таких систем відносяться друкарські фарби, конденсовані змазки, деякі сажонаповнені гумові суміші;

• квазітропні системи, у яких відсутня явно виражена межа текучості.

Істинно-тіксотропні системи - системи, специфічні особливості яких полягають в існуванні гістерезису в’язкісних властивостей.

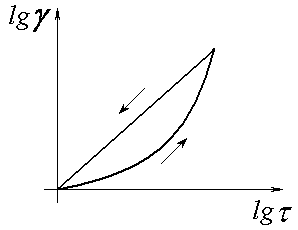
Рис. 5.2. Гістерезис в’язкісних властивостей

γ- швидкість зсуву; τ - напруження зсуву.

Структурна особливість істинно-тіксотропних систем полягає в тому, що в них існує стійка просторова сітка, утворена силами міжмолекулярної взаємодії.

Такий просторовий каркас володіє певною зсувною міцністю. Тому істинно-тіксотропні системи навіть при великих деформаціях поводять себе як тверді тіла. Деформація в цих межах повністю зворотна, а напруження які виникають в матеріалі не релаксують до нуля, яким би не був час експерименту.

Для характеристики тіксотропних властивостей істинно-тіксотропних систем використовують такі параметри:

а) відношення критичного напруження зсуву , який характеризує міцність просторової структури, до значення напруження зсуву , який відповідає встановленому режиму течії із заданою швидкістю деформації:

(5.2.)

б) часова (деформаційна) залежність відношення ефективної в’язкості частково зруйнованої структури до ефективної в’язкості системи, яка відповідає встановленому режиму течії :

(5.3.) , (5.4.)

де γ - деформація зсуву.

Квазітіксотропні системи

Специфічна особливість квазітіксотропних систем полягає в тому, що в’язкісні властивості системи, починаючи з певного значення швидкості деформації залежать не тільки від швидкості деформації, але й від абсолютної величини деформації. До квазітіксотропних систем відносяться більшість каучуків та розплавів полімерів. В квазітіксотропних системах відсутній стійкий просторовий каркас, тому, при малій швидкості навантаження, напруження, які виникають в полімері, встигають релаксувати: течія такої системи (в області малих швидкостей деформації) відбувається без будь-яких помітних руйнувань надмолекулярної структури.

Антитіксотропні середовища

Термін „антитіксотропія” введений для визначення явища зростання ефективної в’язкості в результаті деформації. Представляє собою дуже рідкісне явище. Наприклад, таке явище виявлене в 5% розчині поліметакрилової кислоти у воді.

Реопектичні середовища

Антитіксотропія та реопексія супроводжуються зростанням напруження зсуву в процесі деформації. Однак, між ними є різниця. Реопексія – властивість деяких матеріалів поступово структуруватися при механічній дії в умовах невеликих швидкостей зсуву. При подальшому збільшенні швидкості зсуву матеріал стає тіксотропним. Матеріали називають реопектичними.

Реопектичні та тіксотропні матеріали є реологічними середовищами з характеристиками, які є функціями часу. Для даних середовищ характерна наступна функціональна залежність:

. (5.5.)

Тобто, напруження визначається не тільки швидкістю зсуву, але і його тривалістю.

В’язкопружні середовища

При течії в’язкої рідини вся механічна енергія, яка підводиться до неї ззовні, повністю дисипує в теплоту. Ідеально пружні тіла при їх деформуванні здатні накопичувати надану їм енергію, і знову повертати її при знятті навантажень.

Існують середовища, які володіють одночасно як властивостями в’язкої рідини так і властивостями пружного тіла. Вони називаються в’язкопружними. Типовим прикладом таких рідин є максвелівська рідина, яка характеризується наявністю спектра релаксації. До таких середовищ можна віднести розчини і розплави більшості термопластів та колоїдні систем, які володіють деякою пружністю форми.

Для таких матеріалів, залежність між діючим напруженням і викликаною деформацією має складний вигляд. Це пояснюється тим, що під дією напруження, крім миттєвої пружності, яка властива цим середовищам може мати місце явище запізнілої пружності і течія, що обумовлює виникнення зворотніх в часі та остаточних деформацій.

Такі середовища називають лінійно-в’язкопружними, так як вони описуються лінійною залежністю між напруженням, деформацією та їх похідними в часі.

Якщо напруження, що діє у в’язкопружному середовищі – , а деформація – , то лінійно-в’язкопружна залежність може бути записана як:

, (5.6.)

де - лінійні диференціальні оператори.

Залежність деформацій від часу при дії постійного напруження для нелінійно-в’язкопружних тіл приведена на рис. 5.3.

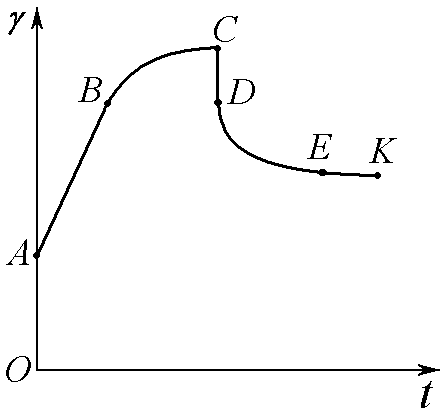
Рис. 5.3. Залежність деформацій від часу при

для нелінійно-в’язкопружних тіл

Після деформації, викликаної миттєвою пружністю, слідує деформація, викликана запізнілою пружністю та течією (ділянка ). Потім ділянка , яка визначає деформацію обумовлену однією течією. При знятті напруження відбувається відновлення миттєвої пружності деформації (відрізок ). Деформація, обумовлена запізнілою пружністю, відновлюється з часом ( точки та ).

Остаточна деформація, пов’язана з течією середовища, показана на кривій відрізком . Найбільш точною математичною моделлю лінійно-в’язкопружного середовища є модель Максвела.

Якщо між напруженням та деформацією немає лінійної залежності, то середовище називають нелінійно-в’язкопружним.

Лекція 6