16. Методика расчёта средней арифметической (простой и взвешенной).
Средняя арифметическая – наиболее распространённый вид средней. Она исчисляется в случаях, когда объём осредняемого признака образуется как сумма его значений у отдельных единиц совокупности. Например, требуется вычислить средний стаж десяти работников предприятия, причём дан ряд одиночных значений признака 6, 5, 4, 3, 3, 4, 5, 4, 5, 4. Тогда объём осредняемого признака
а среднее значение вычисляется по формуле простой средней
Если те же данные сгруппированы по величине признака, то среднее значение вычисляется по формуле взвешенной средней
17. Методика расчёта средней арифметической взвешенной в дискретном и интервальном рядах распределения.
Если те же данные сгруппированы по величине признака, то среднее значение вычисляется по формуле взвешенной средней
Методы расчёта средних по данным интервальных рядов имеют специфику, связанную с тем, что исследователь имеет дело не с дискретными значениями, а с интервалами группировочного признака. В этих случаях определения степенных средних сохраняются с учётом, что вместо значений вариант в них подставляются серединные значения интервалов.
Для расчёта моды по данным интервального ряда используется следующая формула:
где
- нижняя граница модального интервала;
- размер модального
интервала;
- частота модального
интервала;
- частота интервала,
предшествующего модальному;
- частота интервала,
следующего за модальным.
Для расчёта медианы в интервальном ряду используется следующая формула:
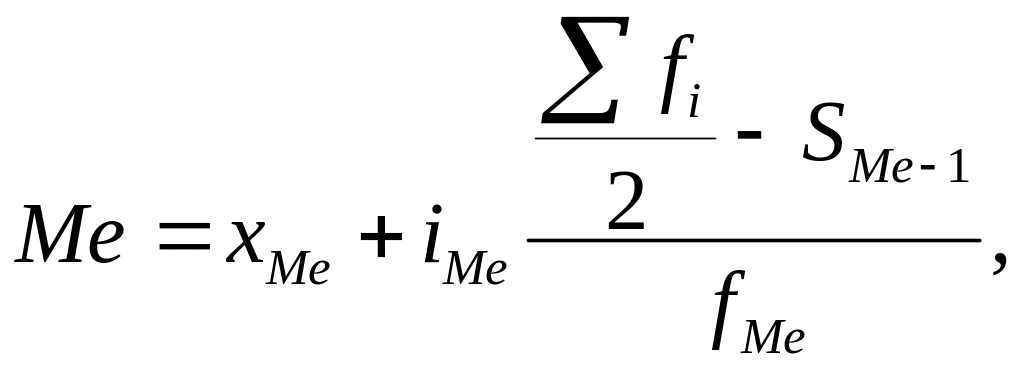
где
- нижняя граница медианного интервала;
- размер медианного
интервала;
- сумма накопленных
частот до медианного интервала;
- частота медианного
интервала;
- полусумма частот
ряда.
18. Методика расчёта средней гармонической и область её практического применения.
Средняя
гармоническая величина
чаще всего вычисляется, когда статистическая
информация не содержит частот по
отдельным вариантам совокупности, а
имеются данные по объёмам осредняемого
признака, относящимся к отдельным
вариантам совокупности. Например,
необходимо вычислить среднюю цену
единицы товара, причём даны объёмы
реализации по каждому виду товара
в виде ряда 600, 1000, 850 (тыс. руб.) и
соответствующие цены по каждому виду
товара
в виде ряда 20, 40, 50 (тыс. руб./шт.). Тогда
средняя цена вычисляется по формуле
средней гармонической взвешенной
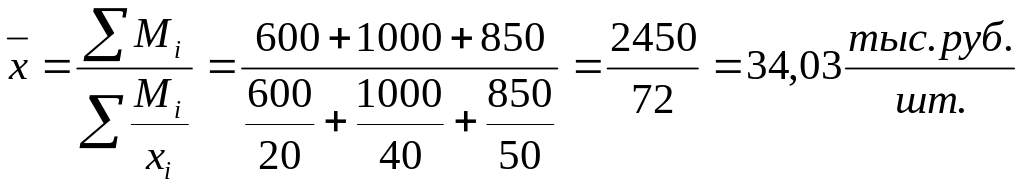
Можно видеть,
что средняя гармоническая является
превращённой (обратной) формой средней
арифметической. Вместо средней
гармонической всегда можно рассчитать
среднюю арифметическую, но для этого
сначала нужно определить веса
отдельных значений признака.
19. Средняя геометрическая: методика расчёта и область практического применения.
0 |
Средняя геометрическая |
|
|
При использовании формулы средней геометрической индивидуальные значения признака, как правило, представляют собой относительные величины динамики, построенные в виде цепных величин (как отношения последующих уровней показателя к предыдущим уровням в ряду динамики), причём временные отрезки ряда динамики одинаковы (сутки, месяц, год). Средняя геометрическая величина характеризует, таким образом, средний коэффициент роста. Например, для данных ряда динамики, представленных в табл.10,
Табл.10. Ряд динамики роста доходов населения
-
Год
2000
(базовый)
2001
2002
2003
Отношение доходов последующего периода к предыдущему
1
1,04
1,144
1,35
средний темп роста доходов населения вычисляется по формуле средней геометрической простой
