1.2. Методы расчета переходных процессов, функции веса и построения графиков переходных процессов

Понятие переходного процесса является одним из важнейших понятий ТАУ, и особенно теории линейных систем. Поэтому умение легко, практически автоматически, рассчитывать переходный процесс во многом определяет успех дальнейшего понимания ТАУ.

Как известно, передаточная функция звена – это отношение изображения по Лапласу выходного сигнала к изображению входного, которыми в частном случае могут быть переходный процесс h(p) и единичный сигнал 1(p)=1/p,

Из этого следует, что изображение переходного процесса

(1.9)

Аналогично для функции веса

и (1.10)

По свойству преобразования Лапласа, умножение изображения на p, соответствует первой производной от оригинала. Поэтому функция веса определяется также как производная от переходного процесса:

(1.11)

Заметим еще раз, что все функции комплексной переменной p - h(p), k(p) и т.д., являются изображениями соответствующих функций действительной переменной t - h(t), k(t) и т.д.

Примеры расчетов переходных процессов и функции веса

Далее расчёты переходного процесса, функции веса с построением их графиков выполним на числовых примерах.

Вид переходного процесса определяется корнями характеристического уравнения, образуемого приравниванием к нулю либо многочлена знаменателя передаточной функции, либо сомножителя при у(р) в операторном уравнении.

I. Корни характеристического уравнения действительные.

Пусть задана передаточная функция САУ

Решение.

1. Раскладываем знаменатель на простейшие сомножители

Решаем относительно p характеристическое уравнение

Оно имеет следующие действительные корни:

Следовательно, характеристический многочлен можно разложить на множители следующим способом:

(1.12)

2. Определяем оригинал табличным способом

Представляем выражение h(p) в виде суммы простейших дробей, оригиналы для каждой из которых имеются в таблице 1.1:

(1.13)

Чтобы коэффициенты при степенях p в левой и правой частях равенства (1.13) были бы одинаковыми, необходимо:

Приравняв коэффициенты при одинаковых степенях p, получаем:

Решая, эту систему уравнений, получаем:

Окончательно получаем разложение h(p) на табличные выражения:

Перейдя согласно табл.1.1 от изображений к оригиналам, получим:

(1.14)

и для функции веса:

(1.15)

3. Строим графики переходного процесса и функции веса

Для построения графика надо определить время счета и шаг изменения времени.

Определение времени счета

Приводим выражение h(t) к стандартному виду, так что бы свободный член был равен 1:

(1.16)

На бесконечности значение h(t) стремится к установившемуся значению h_уст=3, так как обе экспоненты в выражении (1.16) обращаются в нуль.

Находим время переходного процесса для каждой из экспонент.

Переходный процесс считается завершенным, когда его график h(t) попадает в 5%-зону установившегося значения, и далее не выходит из нее. В представлении переходного процесса в виде (1.16) установившееся значение для выражения, заключённого в скобки, равно 1. Поэтому время t_пп1, в течение которого затухает 1-я экспонента, находится из уравнения

Аналогично находим время переходного процесса для 2-й экспоненты:

Время t_пп всего переходного процесса не равно ни t_пп1, ни t_пп2, но меньше большего из этих двух значений. Точное значение t_пп можно найти только из графика переходного процесса. Для аналитического его определения потребовалось бы решить трансцендентное уравнение, что невозможно.

Определение шага вычислений

Шаг вычислений Δt выбираем таким образом, чтобы объём вычислений был минимальный и достаточный для построения графика. Здесь используется практическое правило: для построения гладкого графика вручную достаточно иметь 5-10 точек графика, через которые затем "на глаз" проводится весь график.

Согласно оценке (1.17) времени t_пп1 для построения составляющей графика h(t), соответствующей 1-й экспоненте, шаг вычислений Δt₁ должен быть равен 0,32...0,64 с. Аналогично, основываясь на оценке t_пп2, находим Δt₂=0,04...0,08 с. Поэтому в интервале изменения t от 0 до 0,4 с вычисления ведём с шагом Δt₁=0,08 с, а далее до времени 3,2 с - с шагом Δt₂=0,4 с.

Функцию веса k(t) рассчитываем по выражению (1.15) при тех же значениях t, которые использовались при вычислении h(t).

Результаты вычислений сводятся в таблицу 1.2.

Таблица 1.2

t	0	0,08	0,16	0,24	0,32	0,4	0,8	1,2	1,6	2	2,4	2,8	3,2
h(t)	0													3
k(t)	1													0

По данным этой таблицы строятся графики h(t) и k(t) (рис.1.5).

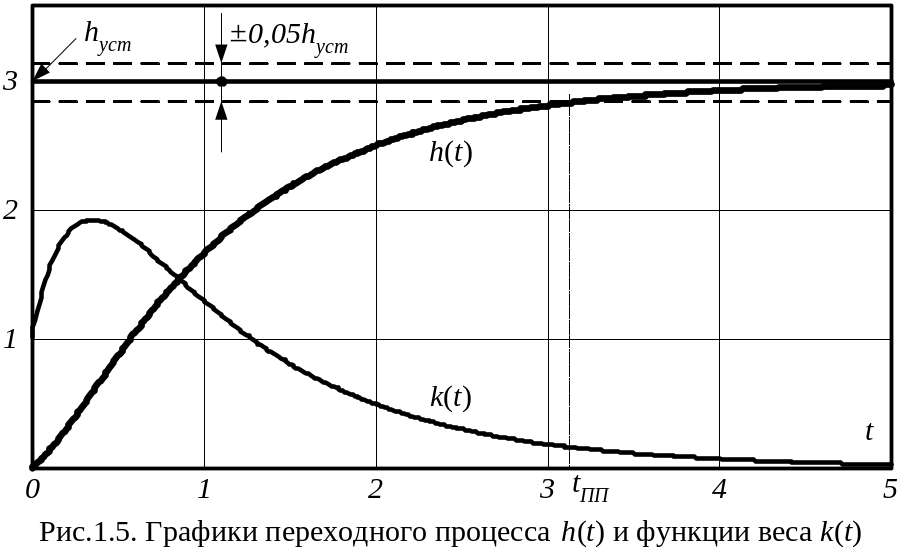
II. Корни характеристического уравнения комплексные

Этапы расчётов те же, что и в предыдущем примере, поэтому нумерацию этапов и названия далее не приводим.

Пусть задана передаточная функция

Решаем характеристическое уравнение

Корни комплексные, поэтому далее решение идет по другому пути.

Выделяем полный квадрат в знаменателе, а затем, как и раньше раскладываем выражение h(p) на сумму табличных выражений:

Из равенства второй и последней дробей получаем систему уравнений, использемую для расчета значений коэффициентов А, В и С,

Решая, эту систему уравнений, получаем:

Окончательно изображение переходного процесса примет вид:

Переходим согласно табл.1.1 от изображений к оригиналам:

(1.17)

Далее находим функцию веса:

(1.18)

Определение времени счета:

Преобразуем выражение h(t) (1.17) следующим образом:

(1.19)

Сумму в скобке можно представить в виде одной функции sin:

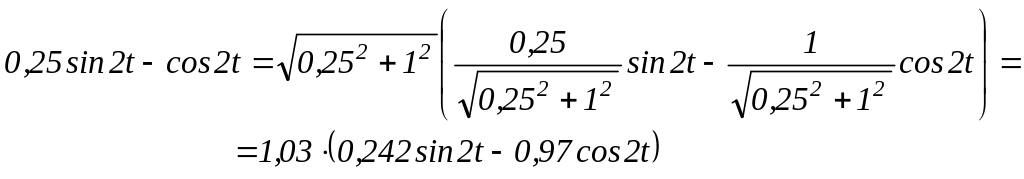(1.20)

Мы имеем право на замену дробей 0,242 и 0,97 на cos и sin, соответственно, т.к. сумма их квадратов равна 1: 0,242²+0,97²=1. Это свойство коэффициентов при sin t и cos t (в данном случае ) в выражении (3.28) верно всегда при выполнении преобразований, приведенных в этом выражении.

C учетом (1.20) h(t) можно представить в таком виде:

,

где рад (вычислить  можно по любой формуле из приведенного их ряда).

Окончательно:

(1.21)

Так как функция sin по модулю не превосходит 1, то время переходного процесса можно вычислить так же, как и раньше, из уравнения:

(1.22)

График переходного процесса колебательный и будет содержать экстремальные точки. Для их нахождения используется производная от h(t), т.е. функция веса k(t):

k(t)=0, 1,875e^-0,5tsin2t+e^-0,5tcos2t=0, tg2t=-1/1,875=-0,533,

откуда

t_e=(arctg(-0,533)+n)/2=-0,245+n/2 (рад), где n=1,2,3...

Значения t_e: t_e1=1,325 c, t_e2=2,9 c; t_e3=4,465 c, t_e4=6,03 c и т.д.

Определение шага вычислений:

Из времени t_пп=6,1 с находим шаг вычислений  t=1с; Время счета t=0..7.

Далее заполняется таблица (табл.1.3) вычислений при найденных значениях t и затем строятся графики h(t) и k(t) (рис.1.6).

Таблица 1.3

t	0	1,325	2	2,9	3,7	4,465	5	6,03	7	∞
h(t)	0									1
k(t)	1									0