3.3.3. Структурная группа 2-го класса, 3-го вида

Рассмотрим условие равновесия звена 3 (рис. 3.9)

, (3.5)

где сила задана.

Из условия равенства нулю всех моментов сил звена 3 относительно точки В находим силу , предполагая, что без учета трения ее вектор перпендикулярен АВ:

; ,

где h₃ – плечо момента силы P₃; .

Отсюда .

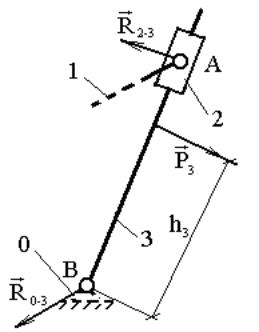
Рис. 3.9. План структурной группы

2-го класса, 3-го вида

Силу реакции между звеньями 1 (кривошипом) и 2 (ползуном) находим из условия . Силу реакции R_0-3 между коромыслом 3 и станиной можно найти, построив план сил, используя уравнение (3.5) равновесия звена 3.

3.3.4. Силовой анализ ведущего звена

Вариант 1

(ведущее звено – зубчатое колесо или кривошип)

На изображенном плане кривошипа (рис. 3.10) сила реакции в кинематической паре А , Р_ур ОА.

Силу берём из силового анализа, проведённого ранее для присоединённой к кривошипу структурной группы. Сила реакции || OA (исходя из теоремы о трёх силах, в соответствии с которой линии сил, действующих на тело, находящееся в равновесии, пересекаются в одной точке. В данном случае это точка А).

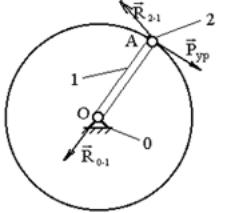
Рис. 3.10. План кривошипа с приложенными силами

Условие равновесия звена 1 (кривошипа):

. (3.6)

Строим план сил звена 1 в масштабе (рис. 3.11), предварительно записав уравнение равновесия (3.6) в виде векторных отрезков:

.

Уравновешивающая сила вычисляется по формуле:

,

а реакция в кинематической паре О – по формуле:

,

где величины и берутся измерением на плане сил (рис. 3.11).

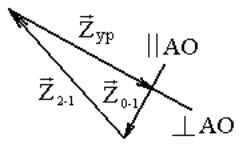
Рис. 3.11. План сил кривошипа

3.4. Теорема о «жёстком» рычаге Жуковского

При определении мощности, расчете на ведущем валу и других задачах необходимо знать только уравновешенную силу, приложенную к начальному звену. В таких случаях применяется теорема Жуковского.

Теорема Жуковского основана на принципе возможных перемещений: сумма элементарных работ внешних сил на их возможных перемещениях равна нулю.

Теорема используется для определения уравновешивающей силы или уравновешивающего момента без предварительного определения реакций в кинематических парах механизма и является графической интерпретацией принципа возможных перемещений точек приложения сил. Для реального механизма эти возможные перемещения являются реальными.

Исходя из принципа сохранения энергии сумма работ всех внешних сил, приложенных к звеньям механизма, равна нулю. Это условие можно записать в виде:

, (3.7)

где P_i – все внешние силы, в том числе силы полезного и вредного сопротивления, силы инерции и веса, действующие на звенья механизма (силы реакции здесь не учитываются); dS_i – элементарные перемещения точек приложения этих сил; _i – угол приложения внешних сил, или угол давления (угол между вектором силы и вектором скорости).

Разделим уравнение (3.7) на бесконечно малый интервал времени dt и получим (при условии, что dS/dt = ):

, (3.8)

то есть сумму мгновенных мощностей, равную нулю.

Для определения величины мгновенных мощностей можно выполнить решение следующей графической интерпретации. Дано звено ВС с известной скоростью точки D и приложенной к этой точке силой (рис. 3.12). Построим план скоростей, повёрнутый на 90⁰, где , . Вычислим момент силы относительно полюса Р_v плана скоростей:

.

С учётом этого уравнение (3.8) можно записать как .

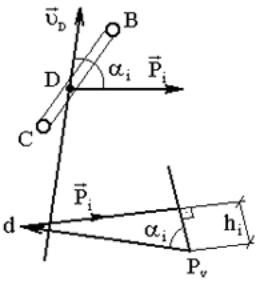
Рис. 3.12. План звена с повёрнутым

на 90⁰ планом скоростей

Так как масштаб , то можно сформулировать теорему Жуковского:

, (3.9)

или алгебраическая сумма моментов всех внешних сил, перенесенных с механизма в соответствующие точки повёрнутого на 90⁰ плана скоростей, относительно полюса равна нулю.

Последовательность определения P_ур в механизме по теореме Жуковского:

1. Построить повёрнутый на 90⁰ (в любую сторону) план скоростей механизма.

2. В соответствующие точки плана скоростей нанести все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу P_ур.

3. Составить уравнение вида (3.9). Плечи моментов сил брать из повёрнутого плана скоростей.

4. Из составленного уравнения определить P_ур.

Пример

Заданы внешние силы, действующие на звенья механизма Р₂ и Р₃. Найдём уравновешивающую силу Р_ур, для чего построим план механизма в масштабе длин (рис. 3.13) и повёрнутый на 90⁰ план скоростей (рис. 3.14).

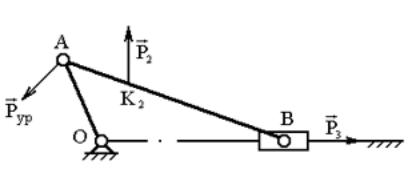
Рис. 3.13. План механизма

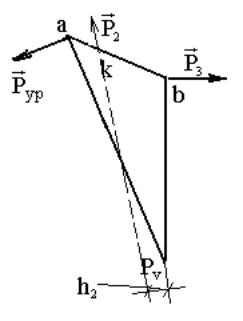
Рис. 3.14. Повёрнутый на 90⁰ план скоростей

Приложим силы в соответствующие точки k и b₃ повёрнутого плана скоростей, обозначаем плечи сил. Составляем уравнение моментов сил относительно полюса плана скоростей:

.

Отсюда:

.

Если сила P_ур получается с отрицательным знаком, то её предварительно выбранное направление следует поменять на противоположное.