Р ешение

ЭДС генератора E = U_х = 110 В, внутреннее сопротивление генератора r_в = 0,25 Ом, расчётный ток короткого замыкания для рабочего участка внешней характеристики J_k = = = 440 А. Схема замещения генератора с последовательным включением источника ЭДС E = 110 В и сопротивления r_в = 0,25 Ом приведена на рис. 1.13,а; схема с параллельным включением источника тока и сопротивления приведена на рис. 1.13,б.

Для последовательной схемы замещения в соответствии со ІІ законом Кирхгофа получаем ir_H + ir_в = Е.

У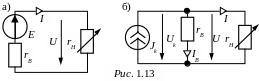 множим всё это выражение на ток цепи i и получим

i ²r_H + i ²r_в = Еi. (1.1)

В соответствии с законом Джоуля-Ленца

i ²r_H = Р_H – мощность, потребляемая нагрузкой,

i ²r_в = Р_в – мощность, рассеиваемая в виде тепла во внутреннем сопротивлении генератора,

Еi = Р_Г – мощность, развиваемая генератором (источником ЭДС).

Выражение (1.1) отражает одно из основных свойств электрической це-пи: суммарная генерируемая источниками энергии мощность равна суммар-ной мощности потребителей цепи. Это свойство можно сформулировать так: для электрической цепи выполняется баланс мощностей.

Для параллельной схемы замещения в соответствии с рис. 1.13б на основании І закона Кирхгофа получаем i + i_в = J_k . (1.2)

Для этой схемы напряжение на зажимах источника тока U_k и на зажимах сопротивлений U одинаковы. Умножим полученное выражение (1.2) на U_k = U и получим: Ui + Ui_в = U_kJ_k .

Но по закону Ома U = ir_H, U = i_вr_в и мы приходим к выражению баланса мощностей для схемы с источником тока:

i ²r_H + i ²r_в = Р_Г = U_kJ_k . (1.3)

З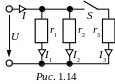 АДАЧА 1.7. Для электрической цепи рис. 1.14 заданы сопротивления r₁ = 100 Ом, r₂ = 150 Ом, r₃ = 50 Ом и напряжение U = 150 B. Рассчитать токи при разомкнутом рубильнике S. Как изменятся токи, если рубильник будет замкнут?

Решение

При разомкнутом рубильнике S токи сопротивлений рассчитаем по закону Ома: i₃ = 0, так как рубильник разомкнут;

i₁ = = = 1,5 A; i₂ = = = 1,0 A;

ток на входе параллельного соединения найдём в соответствии с І законом Кирхгофа i = i₁ + i₂ + i₃ = 1,5 + 1 + 0 = 2,5 A.

При замкнутом рубильнике токи

i₁ = = = 1,5 A – имеет прежнее значение,

i₂ = = = 1,0 A – также не изменится,

i₃ = = = 3 A.

Ток общей части схемы изменится: i = i₁ + i₂ + i₃ = 1,5 + 1 + 3 = 5,5 A.

ЗАДАЧА 1.8. Для приведенной на рис. 1.15 схемы известны показания приборов: вольтметр V показывает 120 В, ваттметр W имеет показание 240 Вт. Известны сопротивления r₁ = 16 Ом, r₂ = 40 Ом. Определить токи, сопротивление r₃, напряжение U. Проверить баланс мощностей.

Решение

В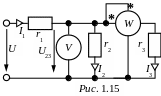 ольтметр V измеряет напряжение U₂₃ = 120 В на участке с параллельным соединением сопротивлений r₂ и r₃. По закону Ома ток i₂ = = = 3 A.

Ваттметр измеряет мощность, потребляемую сопротивлением r₃

P₃ = i₃²r₃ = U₂₃I₃,

поэтому i₃ = = = 2 A, а по закону Ома r₃ = = = 60 Ом.

Ток сопротивления r₁ и источника питания в соответствии с І законом Кирхгофа i₁ = i₂ + i₃ = 3 + 2 = 5 A.

В соответствии со ІІ законом Кирхгофа, записанным для контура r₁-r₂-U, напряжение на входе схемы рис. 1.15

U = i₁r₁ + U₂₃ = 516 + 120 = 200 В.

Мощность генератора P_г = Ui₁ = 2005 = 1000 Вт.

Суммарная мощность потребителей

 P_п = i₁²r₁ + i₂²r₂ + i₃²r₃ = 5²16 + 3²40 + 2²60 = 400 + 360 + 240 = 1000 Вт.

Так как баланс мощностей P_г =  P_п выполняется, задача решена верно.

ЗАДАЧА 1.9. В схеме рис. 1.16 ток i₄ = 8 A измерен амперметром магнитоэлектрической системы. Часть параметров схемы известна:

E₁ = 120 В, E₄ = 80 В, E₅ = 6 В, r₂ = r₄ = 6 Ом, r₃ = r₅ = 2 Ом, r₆ = 3 Ом.

Определить остальные токи, найти сопротивление r₁. Для наружного контура построить потенциальную диаграмму.