Решение
Используем следующие столбцовые матрицы:
- токи ветвей [I] = [I2, I3, I1, I4]T;
- токи источников тока [J] = [0, 0, 0, -J]T;
- обобщённые токи ветвей [Iв] = [I] + [J] = [I2, I3, I1, I4 – J]T;
- напряжения ветвей [U] = [U2, U3, U1, U4]T;
- ЭДС ветвей [E] = [E2, 0, E1, 0]T;
- обобщённые напряжения ветвей [Uв] = [U] – [E] = [U2-Е2, U3, U1-Е1, U4]T.
Матрица
соединений:
[A]
=
.
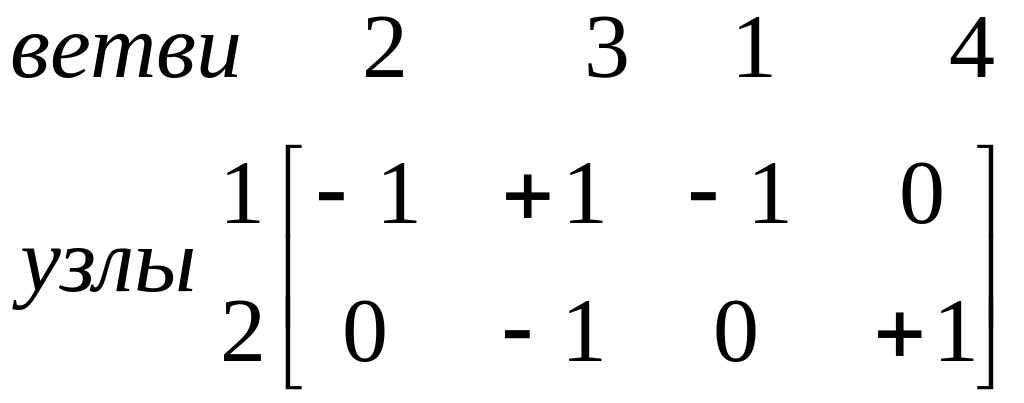Уравнения по первому закону Кирхгофа:
[A][Iв]
=
=
0,
т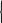
о
есть
-I2
+ I3
– I1
= 0, (*)
-I3 + I4 – J = 0.
Или [A][I] = -[A][J]:
=
-
.
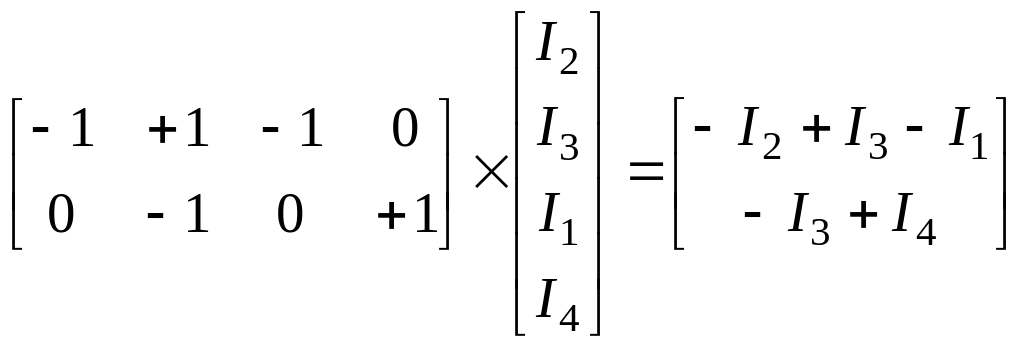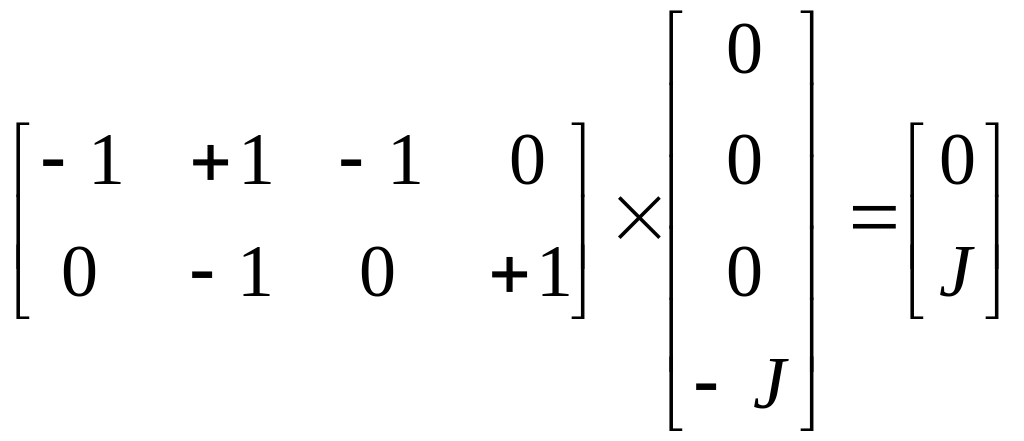Диагональная матрица сопротивлений
[Z]
=
=
.
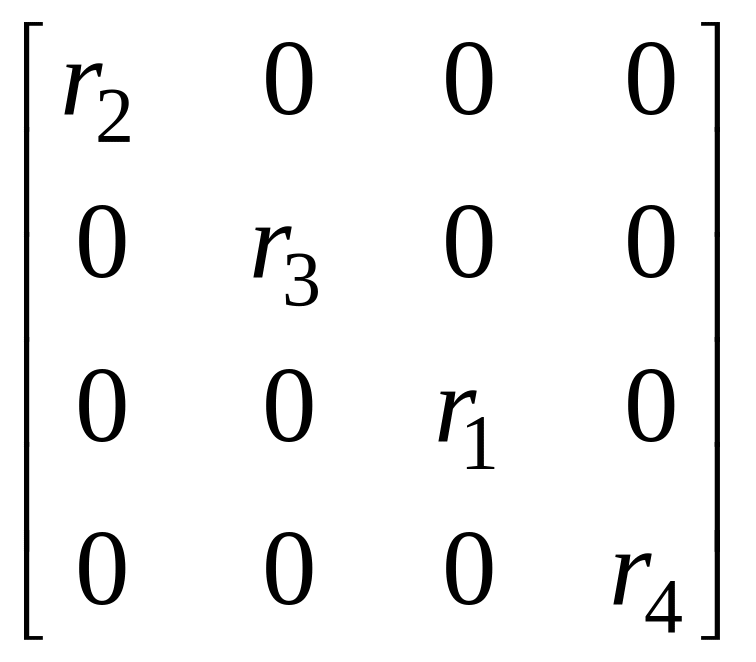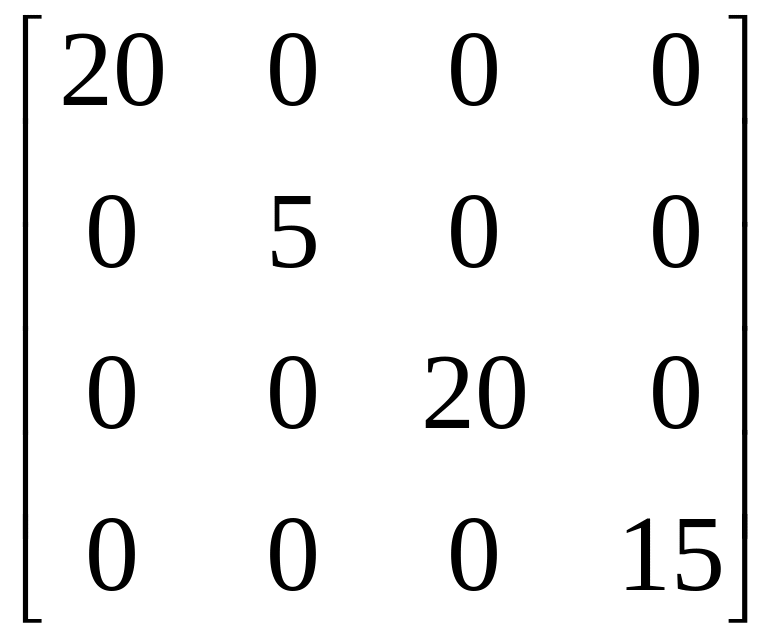Получим матрицу главных контуров. Сначала представим матрицу соединений в виде двух подматриц:
[A]
=
[А1,
A2],
где
[A1]
=
и
[A2]
=
.
Вычислим:
[A1]-1
=
;
-[F]T
= [A1]-1[A2]
=
=
;
[F]
=
.
Матрица
главных контуров:
[В]
=[F,
1]
=
.
Уравнения по второму закону Кирхгофа: [В][Uв] = 0,
[В][Uв]
=
=
=
=
=
0.
Или с учётом [U] = [Z][I] = [r2I2, r3I3, r1I1, r4I4]T
имеем
превращение [Uв]
= [U]
– [Е]
=
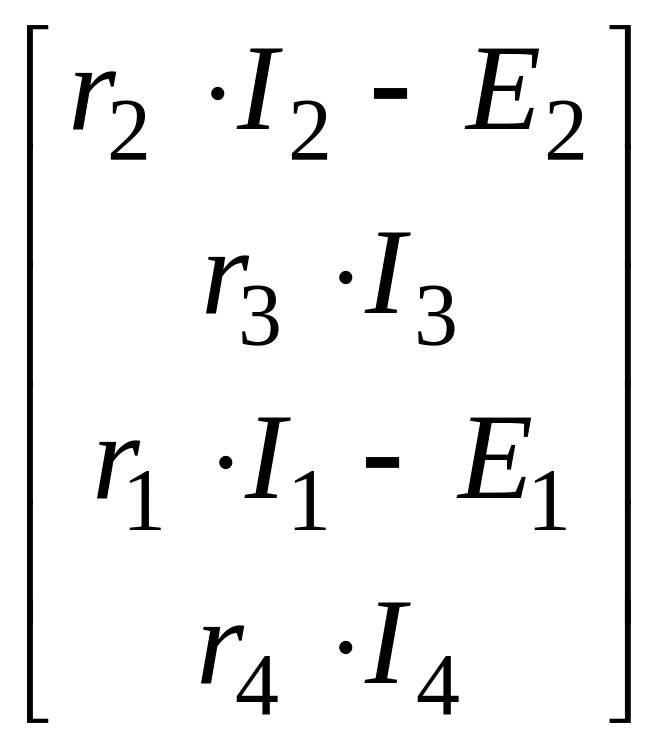и тогда
[В][Uв]
=
=
0.
Таким образом, получаем уравнения:
-
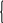r2I2
+ E2
+ r1I1
– E1
= 0 или
r1I1
–
r2I2
= E1
–
E2,
(**)
r2I2 – E2 + r3I3 + r4I4 = 0 r2I2 + r3I3 + r4I4 = E2.
Уравнения (*)-(**) образуют систему уравнений Кирхгофа.