
- •1. Линейные цепи постоянного тока
- •1.1. Основные теоретические положения
- •1.2. Расчёт цепей по законам ома и кирхгофа
- •Решение
- •П олучаем цепь с последовательным соединением резисторов r1-r234-r5.
- •Решение
- •Р ешение
- •Решение
- •Решение
- •Р ешение
- •1.3. Метод уравнений кирхгофа
- •Решение
- •Решение
- •Решение
- •1.4. Метод контурных токов (мкт)
- •Решение
- •Контурные уравнения для контуров:
- •Уравнение баланса мощностей
- •Баланс мощностей сошёлся, задача решена верно.
- •Решение
- •1.5. Метод узловых потенциалов (муп)
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверка правильности решения задачи по I закону Кирхгофа
- •Токи в перемычках рассчитаем по I закону Кирхгофа:
- •1.6. Эквивалентные преобразования электрических цепей
- •Решение
- •1.7. Метод эквивалетного генератора
- •Решение
- •По II закону Кирхгофа для нижнего контура схемы рис. 1.44,а получаем:
- •Искомый ток
- •Что совпадает с ранее полученным значением.
- •Решение
- •1.8. Метод наложения (мн)
- •Решение
- •Решение
- •1.9. Применений матриц к расчёту электрических цепей
- •Решение
- •Решение
Решение
1. Задаёмся положительными направлениями токов в ветвях цепи.
2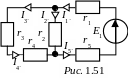 .
Полагаем, что в цепи действует только
ЭДС E1
(рис. 1.51) и определяем токи в ветвях:
.
Полагаем, что в цепи действует только
ЭДС E1
(рис. 1.51) и определяем токи в ветвях:
I5=I1=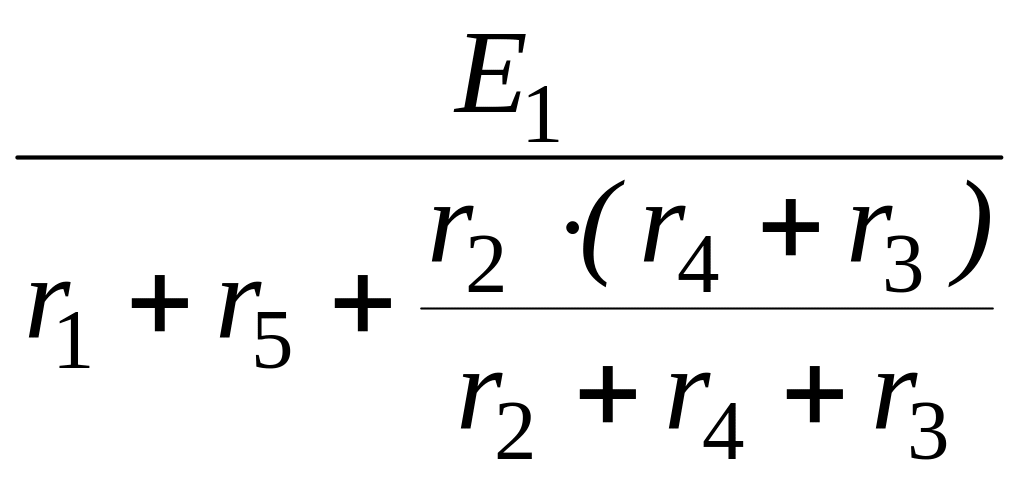 =
=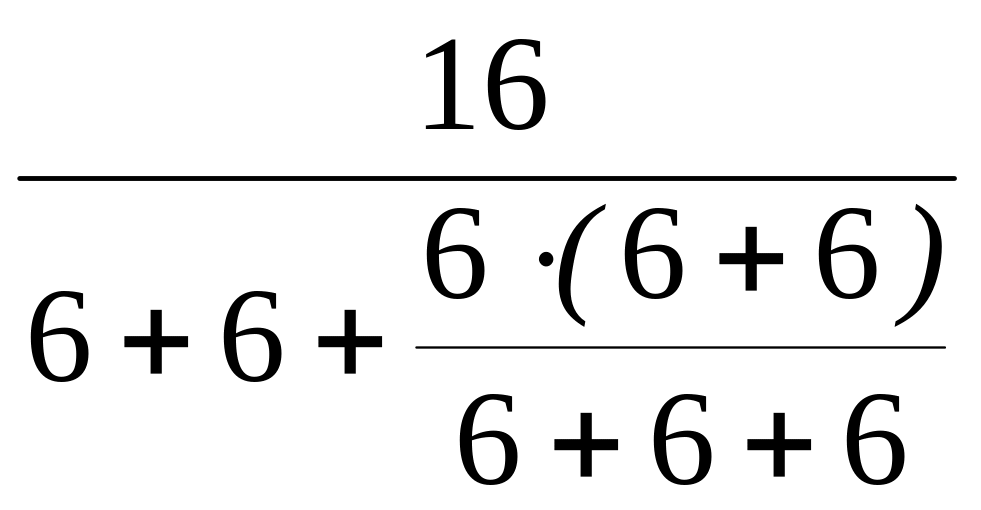 =1
A.
=1
A.
Ток I2 определим по формуле распределения тока в параллельные ветви
I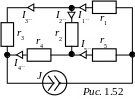 2
= I1
2
= I1![]() =
1
=
1![]() =
0,667 A.
=
0,667 A.
Ток I3 определим по I закону Кирхгофа
I4 = I3 = I1 – I2 = 1 – 0,667 = 0,333 A.
3. Теперь будем считать, что в цепи действует только источник тока J (рис. 1.52) и определим токи от действия этого источника.
Для определения токов в схеме рис. 1.52 преобразуем треугольник сопротивлений r2-r3-r4 в эквивалентную звезду. Учтём, что сопротивления треугольника равны:
r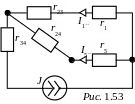 23
= r24
= r34
=
23
= r24
= r34
=![]() =
=![]() =
2 Ом.
=
2 Ом.
В результате преобразования получим эквивалентную схему рис. 1.53, откуда определим токи I1 и I5:
I1
= J![]() =
1
=
1![]() =
0,5 А,
=
0,5 А,
I5 = J – I1 = 1 – 0,5 = 0,5 A.
Из схемы рис. 1.52 с использованием II закона Кирхгофа для контура r1-r2-r5 определим ток I2:
r1I1
+ r2I2
– r5I5
= 0, откуда
I2
=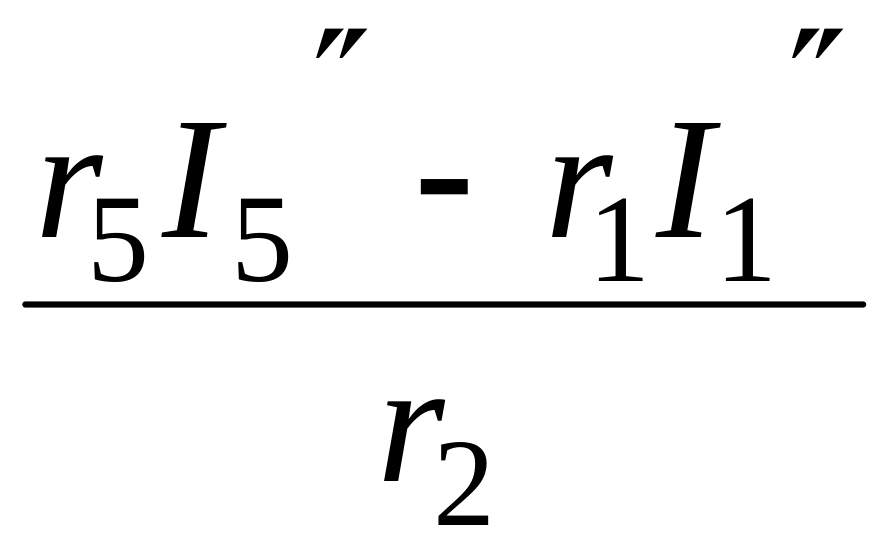 =
0.
=
0.
По I закону Кирхгофа определим оставшиеся токи:
I4 = I2 + I5 = 0,5 A, I3 = I1 – I2 = 0,5 A.
4) По принципу наложения определим полные токи в ветвях
I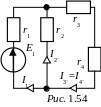 1
=
I1
+ I1
= 1 + 0,5 = 1,5 A,
I2
=
-I2
– I2
= 0,667 A,
1
=
I1
+ I1
= 1 + 0,5 = 1,5 A,
I2
=
-I2
– I2
= 0,667 A,
I3 = I3 + I3 = 0,333 + 0,5 = 0,833 A,
I4 = I4 – I4 = 0,333 – 0,5 = -0,167 A,
I5 = I5 – I5 = 1 – 0,5 = 0,5 A.
ЗАДАЧА 1.49. В условиях задачи 1.18 (рис. 1.26) определить токи по методу наложения.
Решение
1) Определим токи от воздействия источника E1 (рис. 1.54):
I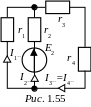 1
=
1
=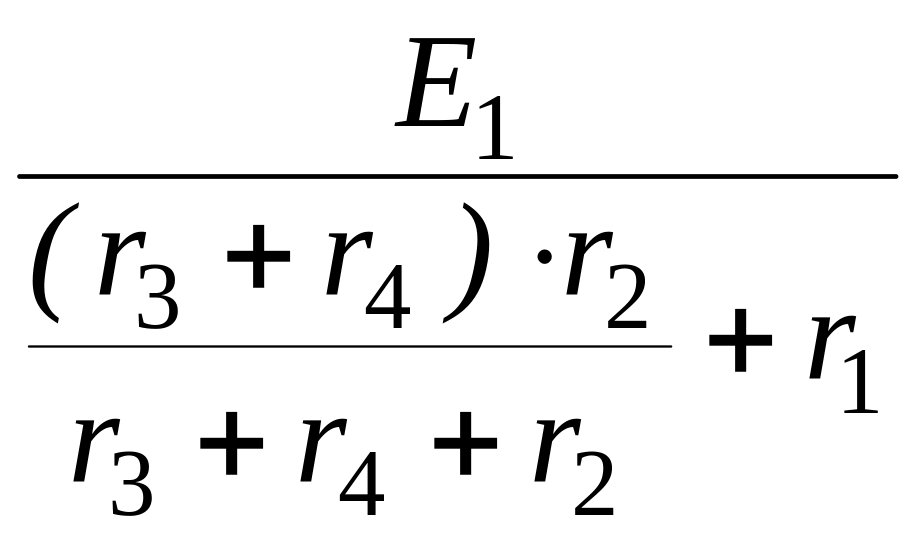 =
=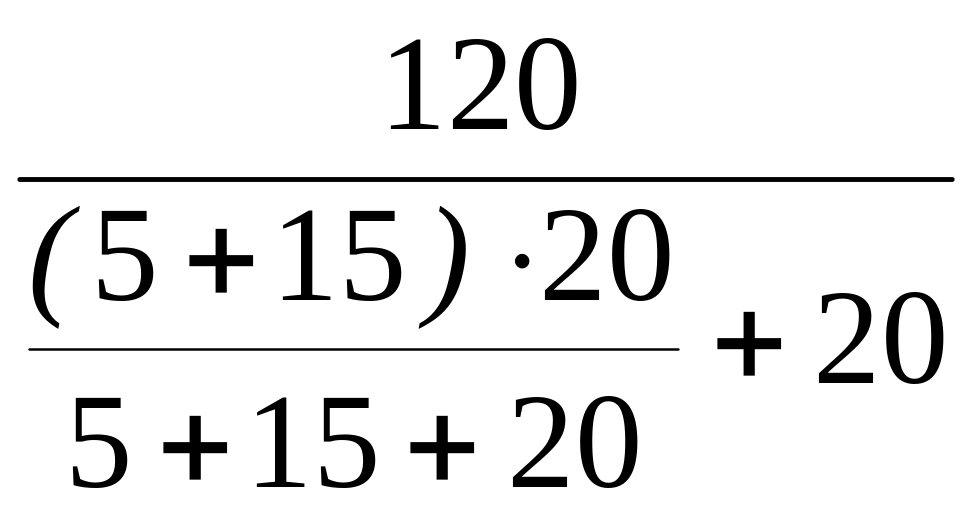 =
4 A,
=
4 A,
I3
=
I4
=
I1![]() =
4
=
4![]() =
2 A,
=
2 A,
I2 = I3 – I1 = 2 – 4 = -2 A.
2) Определим токи от воздействия источника E2 (рис. 1.55). Так как r1 = r2, то схемы рис. 1.54 и рис. 1.55 оказываются идентичными, и поскольку E2 = 0,5E1, то частичные токи схемы рис. 1.55 оказываются в 2 раза меньше соответствующих токов схемы рис. 1.54:
I2 = 0,5I1 = 2 A, I1 = 0,5I2 = -1 A, I3 = I4 = 0,5I3 = 1 A.
3) Определим токи от воздействия источника тока J (рис. 1.56):
I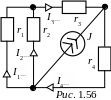 4
=
J
4
=
J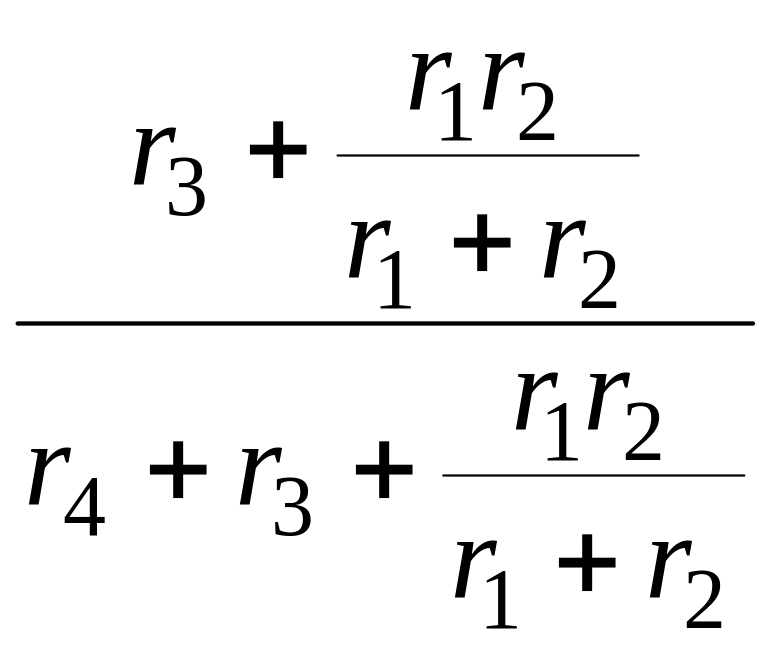 =
4
=
4![]() =
2 A,
=
2 A,
I3 = I4 – J = 2 – 4 = -2 A.
Так как r1 = r2, то I1 = I2 = 0,5I3 = -1 A.
4) По принципу наложения определяем полные токи:
I1 = I1+ I1+ I1 = 4 – 1 – 1 = 2 A, I3 = I3+ I3+ I3 = 2 + 1 – 2 = 1 A,
I2 = I2+ I2+ I2 = -2 + 2 – 1 = -1 A, I4 = I4+ I4+ I4 = 2 + 1 + 2 = 5 A.
ЗАДАЧА 1.50. Решить задачу 1.34 МН.
ЗАДАЧА 1.51. В условиях задачи 1.17 (рис. 1.25) определить токи во всех ветвях МН.
ЗАДАЧА 1.52. Определить токи МН в условиях задачи 1.14 (рис. 1.22,а).
ЗАДАЧА 1.53. Методом наложения определить токи в условиях задачи 1.26 (рис. 1.32).
1.9. Применений матриц к расчёту электрических цепей
Обратим
внимание на то, что при записи уравнений,
описывающих состояние электрических
цепей, в матричной форме ветви схемы не
должны состоять только из идеальных
элементов таких, как: 1) источник тока,
внутреннее сопротивление которого
принимается бесконечно большим rв=,
gв
=![]() =
0; 2) источник ЭДС, внутреннее сопротивление
которого rв
= 0, а
соответствующая проводимость gв
= rв-1
= ;
3) перемычка, сопротивление которой r
= 0, а g
= .
=
0; 2) источник ЭДС, внутреннее сопротивление
которого rв
= 0, а
соответствующая проводимость gв
= rв-1
= ;
3) перемычка, сопротивление которой r
= 0, а g
= .
Поэтому на первом этапе работы со схемой она подвергается эквивалентным преобразованиям:
1) источники тока переключаются параллельно конечным сопротивлениям других ветвей;
2) источники ЭДС ветвей, состоящих только из этих ЭДС, переносятся за узел электрической цепи;
3) узлы, соединённые перемычками, объединяются в единый узел.
П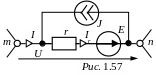 осле
таких преобразований исходной схемы в
новой расчётной схеме будут только
обобщённые ветви вида рис. 1.57.
осле
таких преобразований исходной схемы в
новой расчётной схеме будут только
обобщённые ветви вида рис. 1.57.
На этой схеме: точки «m» и «n» – конечные точки ветви, становящиеся узлами разветвлённой цепи, потенциалы этих точек, соответственно, m и n; напряжение ветви U = m – n; ток обобщённой ветви (в дальнейшем ток ветви) I, положительное направление которого выбирается обязательно совпадающим с положительным направлением напряжения ветви U; Ir – ток сопротивления ветви; E – ЭДС источника ЭДС ветви; J – ток источника тока ветви; r – сопротивление ветви.
Примечание. Указанные на рис. 1.57 направления I, Ir, E, J приняты за положительные. Если по какой-то причине направления некоторых величин будут противоположными тем, которые указаны на рис. 1.57, при передаче цифровой информации необходимо предусмотреть знак «-» перед числом.
ЗАДАЧА 1.54. Для расчёта электрической цепи рис. 1.58,а с выбранным графом, представленным на рис. 1.58,б, составить уравнения по законам Ома и Кирхгофа в матричной форме.
Параметры приведенной электрической цепи заданы:
E1 = 80 В, E5 = 150 В, J2 = 3 A, J3 = 7 A,
r1 = 6 Ом, r2 = 12 Ом, r3 = 15 Ом, r4 = 25 Ом, r5 = 30 Ом, r6 = 8 Ом.
