2.2.6.2 Конические днища.

Р исунок 2.13 – Схема конической оболочки

Для конической обечайки имеем:

R₁ = ; R₂ = x tg;  = ( /2) – ; ctg = tg ; R₁d = dx ,

где  - угол полураствора конуса; X - расстояние точки от вершины конуса.

Преобразуем основные уравнения БТТО применительно к коническим обечайкам. Ограничимся случаем, когда коническая оболочка без нагрузки на краях. Тогда из уравнения равновесия зоны определим меридиональную силу:

SR₂sin² + (X sin + Z cos)sind = Q/2

S xtg sin² = – (X+Z ctg )sin² dx

S = –

S = –

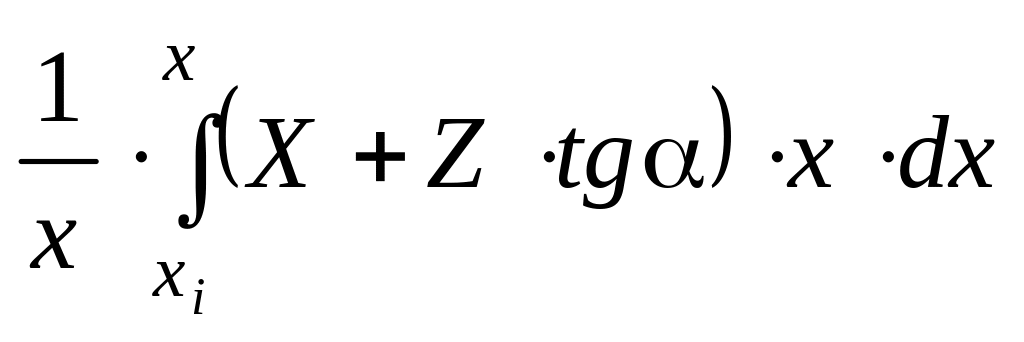
Из уравнения равновесия элемента определим величины кольцевой силы:

S/R₁ + T/R₂ = – Z, T = – ZR₂ = – Z x tg

Если сосуд, нагружен внутренним газовым давлением, то X = 0; Z = – P

Тогда S = – = =

=  ,

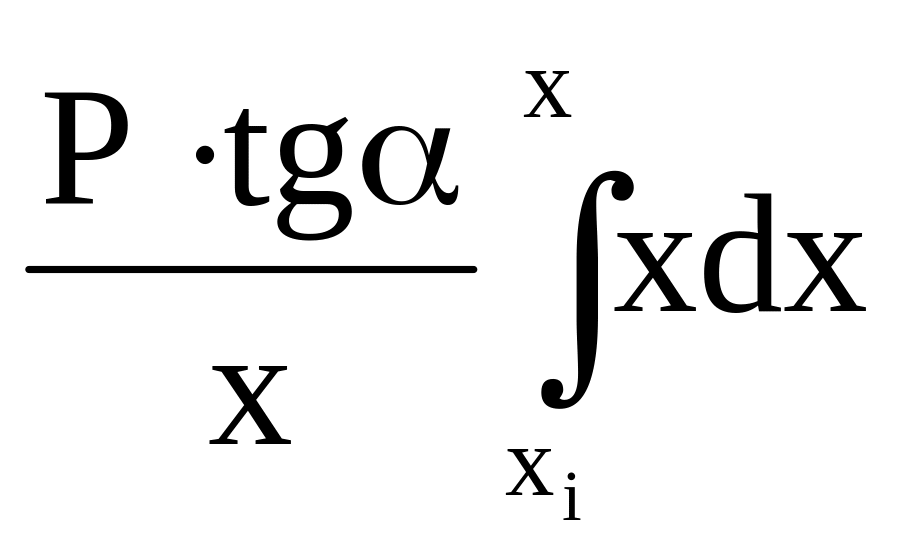а кольцевая сила равна: T = - Z x tg = P x tg.

Если коническая оболочка, нагруженная газовым давлением, и замкнута в вершине, то x_i = 0, тогда:

S = .

Напряжения будут равны:

_S = ; _T =

Следовательно, для конической оболочки, кольцевая напряжения в два раза больше меридиональных.

2.2.6.3 Эллиптическая оболочка.

Рисунок 2.14 – Схема эллиптической оболочки [1]

Для эллиптической оболочки (рис.2.14) с полуосями а и b главные радиусы кривизны рассчитывают следующим образом [1]:

R₁ = ;

R₂ = .

А меридиональные и кольцевые напряжения определяются по следующим формулам:

_S = ; _T = .

2.2.6.4 Плоские днища [1].

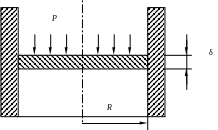
Рисунок 2.15 – Схема нагружения плоского днища.

Главные напряжения, возникающие в плоском днище при такой схеме нагружения рис.2.15, определяются по следующим формулам [1]:

кольцевые напряжения

_T = [(1+ )R² - (1+3 )²],

меридиональные напряжения

_S = [(1+ )R² - (3+ )²],

где δ - толщина плоского днища; R - радиус днища;  - коэффициент Пуассона;  - текущий радиус.

3. Вывод основных уравнений БТТО.

Данный раздел по выводу основных уравнений БТТО представлен в упрощенной форме [3] для студентов заочной формы образования. Основные сведения по геометрии поверхности вращения и допущения к БТТО были изложены в п.2.1 и 2.2.1, которые необходимы для понимания вывода основных уравнений по упрощенной методике.

2.3.1 Вывод уравнения Лапласа.

Рассмотрим оболочку, находящуюся под действием внутреннего давления. Выделим из оболочки элемент двумя меридиональными и кольцевыми сечениями (рис.2.16). Меридиональное сечение – это сечение через ось симметрии; кольцевое – сечение, перпендикулярное к меридиану. На выделенный элемент действуют внутренние и внешние удельные нагрузки, распределенные равномерно по всей толщине оболочки.

Рисунок 2.16 – Элемент оболочки.

К внутренним силам относятся:

- меридиональная сила, действующая на единицу длины параллельного круга серединной поверхности;

- кольцевая сила, действующая на единицу длины меридиана и на всю толщину элемента.

Кроме того, на элемент действует кольцевой и меридиональный изгибающие моменты и поперечная сила (среза). Т.к. в данном случае рассматривается безмоментное состояние оболочки, то изгибающими моментами и силами среза пренебрегаем (в силу их малости).

Обозначим радиус кривизны серединой поверхности меридиональной кривой через R₁. (первый главный радиус), а радиус кривизны серединной поверхности в направлении, перпендикулярном меридиану – R₂ (второй главный радиус).

R₁ = b0  d0; R₂ = aA = bA

Запишем уравнение равновесия элемента в проекциях на нормальn к серединной поверхности оболочки. На грань ab, площадь которой   dy, действует нормальное напряжение (меридиональное напряжение). Сила упругости, вызванная этим напряжением S = _S    dy, действует под углом /2 к нормали n. Поэтому проекция S на нормаль будет равна:

.

Сила, действующая на грань cd, дает на нормаль в точности такую же проекцию.

На гранях ac и bd действует нормальное напряжение (кольцевое). Сила упругости, вызванная этим напряжением,

T = _t  S  dx

действует под углом d/2 к нормали n. Проекция T на нормаль будет равна:

_t    dy  sin(d/2).

Проекция внешней силы на нормаль: P dx dy

Для равновесия элемента необходимо, чтобы алгебраическая сумма проекций сил упругости, а также внешних сил была равна нулю:

Учитывая, что d = dy/R₁, а d = dx/R₂, и заменяя синусы их аргументами, получим уравнение равновесия элемента (уравнение Лапласа):

.

Получим уравнение с двумя неизвестными _S и _T. Для его решения необходимо составить еще уравнение, рассмотрев условие равновесия зоны.