МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

Национальный технический университет

"Харьковский политехнический институт"

Исследование напряжений в элементах тонкостенных аппаратов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу

" Расчет и конструирование машин и аппаратов химических производств"

Харьков 2001

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

Национальный технический университет

"Харьковский политехнический институт"

Исследование напряжений в элементах тонкостенных аппаратов

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

по курсу

" Расчет и конструирование машин и аппаратов химических производств" к практическим и самостоятельным занятиям, курсовой работе, курсовому, бакалаврскому и дипломному проектам для студентов дневной и заочной форм обучение специальностей 7.090220 - "Оборудование химических производств и предприятий строительных материалов", 7.090221 - "Оборудование перерабатывающих и пищевых производств"

Утверждено

редакционно-издательским

советом университета,

протокол №2 от 05.04.2000.

Харьков НТУ "ХПИ" 2001

Исследование напряжений в элементах тонкостенных аппаратов. Методические указания по курсу " Расчет и конструирование машин и аппаратов химических производств" к практическим и самостоятельным занятиям, курсовой работе, курсовому, бакалаврскому и дипломному проектам для студентов дневной и заочной форм обучение специальностей 7.090220 - "Оборудование химических производств и предприятий строительных материалов", 7.090221 - "Оборудование перерабатывающих и пищевых производств" /Сост. В.П. Михайличенко, В.Н. Сидоров, С.О. Белов, Л.Н. Кулик – Харьков: НТУ "ХПИ", 2001. - 28с

Составители: В.П. Михайличенко,

В.Н. Сидоров,

С.О. Белов

Л.Н. Кулик

Рецензент В.О. Лещенко

Кафедра химической техники и промышленной экологии.

К лабораторным работам "Исследование напряжений в элементах тонкостенных аппаратов" по курсу "Расчет и конструирование химических машин и аппаратов" для студентов специальностей 7.090220 и 7.090221.

Авторы: Михайличенко в.П., Сидоров в.Н., Белов с.А., Кулик л.Н.

1 Постановка задачи и цель работы .

В аппаратостроении химической, нефтяной, пищевой и других отраслях промышленности корпуса аппаратов, в большинстве случаев, представляют собой оболочки вращения, в виде цилиндров, шаров, конусов или их комбинаций. Наибольшее распространение получили цилиндрические, сферические, конические, эллиптические и другие оболочки (элементы аппаратов), обладающие хорошей сопротивляемостью давлению среды, простотой конструкции в изготовлении, рациональным расходов материалов и т. д.

В зависимости от величины нагрузок различают тонкостенные и толстостенные оболочки вращения. Подобное деление является условным и критерий тонкостенности должен учитывать требуемую точность расчета. Тонкостенными обычно считают цилиндрические оболочки, имеющие толщину стенки, не превышающую 10% внутреннего диаметра. Такие аппараты обычно эксплуатируются при давлении не более 10 МПа. От действия внутреннего давления в материале тонкостенных оболочек возникают напряжения, величину которых необходимо определить при прочностном расчете аппарата. Эту задачу можно решить, применяя безмоментную (мембранную) теорию тонкостенных оболочек (БТТО).

Чтобы обосновано снижать запасы прочности, повышать точность и надежность расчетов, правильно назначать и полностью использовать применяемые материалы, конструктор должен располагать обширными и хорошо проверенными экспериментальными данными об усилиях и распределении напряжений, фактически действующих, в узлах элементов аппарата. Кроме того, эксперименты дают представление о распределении деформаций и напряжений в элементах сложной конфигурации, не поддающихся расчету.

В современных условиях характер распределения напряжений можно определить методами тензометрирования деформаций и напряжений на моделях или самих машинах. Поэтому целью лабораторных исследований является не только ознакомление студентов с методом измерения деформаций, но и определение на экспериментальной установке напряжений, возникающие в разных точках элементов аппарата и сравнить с напряжениями, рассчитанные на основании БТТО. В случае расхождения экспериментальных и теоретических результатов напряжений необходимо дать объяснения и найти коэффициент корреляции.

2 ТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ БТТО

2.1 Некоторые сведения по геометрии вращения оболочек.

Оболочкой вращения будем называть оболочку, серединная поверхность которой образована вращением какой - либо плоской кривой вокруг оси, лежащей в ее плоскости. Так, сфера образована вращением полуокружности вокруг ее диаметра.

Серединной поверхностью называем поверхность, точки которой везде одинаково отстоят от внутренней и внешней поверхности стенки. Кривая, вращением которой образована серединная поверхность оболочки, называется образующей, а точки пересечения поверхности с осью - полюсами.

Плоскость, проведенная через ось вращения, называется меридиональной, а линия пересечения этой плоскости с поверхностью - меридианом. Нетрудно видеть, что меридианы совпадают с образующей.

Плоскость, проведенная перпендикулярно оси вращения, называется плоскостью параллельного круга, а линия пересечения этой плоскости с поверхностью - параллельным кругом.

Радиус кривизны меридиана, в какой - либо точке поверхности называется первым главным радиусом кривизны и обозначается R₁. Радиус кривизны кривой, полученной от пересечения поверхности плоскостью, перпендикулярной к меридиану называется вторым главным радиусом кривизны поверхности и обозначается R_2.. Концы радиусов кривизны K₁ и K₂ (рис.2.1) называются центрами кривизны. Второй центр кривизны K₂ поверхности вращения лежит на оси оболочки, и оба радиуса на одной прямой, перпендикулярной к поверхности. Угол , образованный осью вращения и главным радиусом называется широтой в данной точке и обозначается .

Рисунок 2.1 – Оболочка вращения.

Пусть r - радиус параллельного круга. На поверхности вращения возьмем элементарный участок с длиной меридиана АВ = dS₁ и длиной параллельного круга AD = dS₂. Тогда из CK₂ P (рис. 2.2) имеем:

r = R₂  sin,

и длина элемента параллельного круга из АСD:

dS₂ = r sin d = R sin d,

принимая sin d  d в силу малости угла d. Длина элемента меридиана из ABK:

dS₁ = R₁ sind = R₁ d

Площадь элементарного участка:

dF = dS₁dS₂ = R₁R₂ sin d d.

2.2 Безмоментная теория тонкостенных оболочек.

В силу громоздкости БТТО ограничимся нахождением основных уравнений, необходимые для лабораторной работы - это уравнение равновесия зоны и уравнение равновесия элемента (уравнение Лапласа).

2.2.1.Некоторые допущения БТТО.

Толщина стенки должна быть весьма малой по сравнению с другими размерами сосуда. Так для цилиндрических оболочек: /R  0.1  0.2, где:  – толщина стенки оболочки; R – внутренний диаметр оболочки.

Вследствие малой толщины стенок можно считать, что растягивающее (сжимающее) напряжения в ней не изменяются по толщине, а величина этих напряжений в R_ВН ∕  раз больше напряжений изгиба. Благодаря этому и можем влиянием моментов не учитывать, т.е. применить БТТО.

По форме сосуд обязательно должен представлять собой оболочку вращения симметричной относительно оси вращения. Нагрузка (давление на стенки) должна быть симметричной относительно оси вращения.

2.2.2 Силы и моменты, действующие в оболочке вращения.

Рассмотрим равновесие элемента оболочки вращения (рис.2.2), выделенного при помощи двух осевых сечений abcd и efgh и двух сечений bcfg и adeh, перпендикулярных к меридиану, проходящему через точку Р.

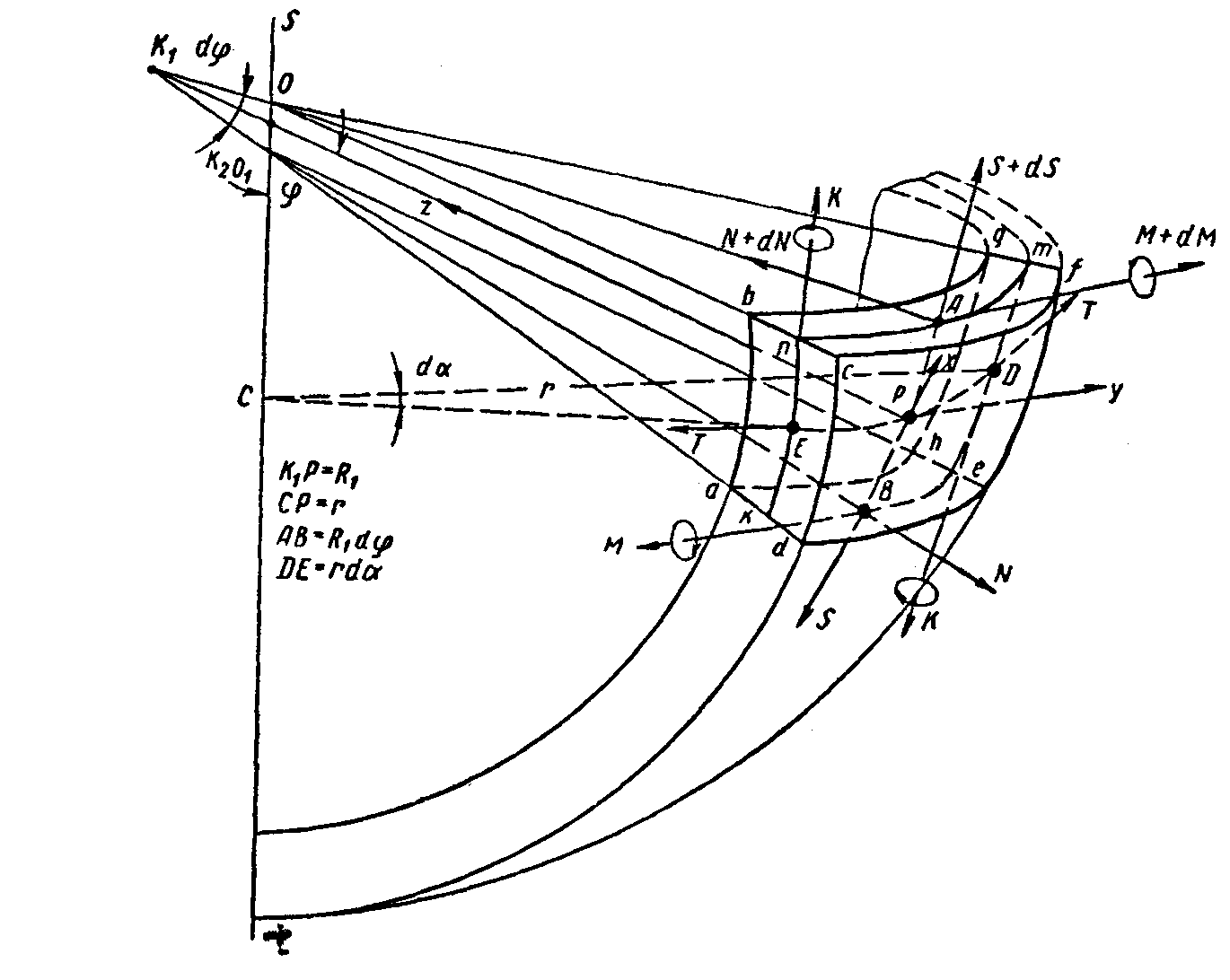
Рисунок 2.2 – Элемент оболочки.

В общем случае на каждую грань оболочки действуют продольные силы (растяжения или сжатия), поперечные силы и изгибающие моменты. Для тонкостенных оболочек, учитывая незначительную по сравнению с радиусами толщину стенок, принимают следующие предпосылки:

1) внутренними силами сжатия (или растяжения), действующими нормально к серединной поверхности оболочки (в направлении радиусов кривизны), можно пренебречь;

2) прямые, нормальные к серединой поверхности оболочки до деформации, остаются такими же и после деформации;

Учитывая, кроме того, симметричность нагрузки вокруг оси, можно заключить, что на грани abcd и efgh действуют одинаковые и обратно направленные нормальные силы и моменты, стремящиеся повернуть грань вокруг касательной к серединному меридиану этих граней. Моментов, лежащих в плоскости этих граней и стремящихся повернуть грани вокруг их центров, не существует, так как если бы такие моменты существовали, они имели бы обратные направления на обеих гранях и стремились бы скручивать выделенный элемент, что по соображениям симметрии невозможно. По аналогичным соображениям на рассматриваемых гранях не может быть и поперечных сил. На грани adeh и bcfg могут действовать лишь моменты, стремящиеся повернуть эти грани вокруг касательных к параллельным кругам, проходящим через центры граней, нормальные силы, направленные вдоль меридиана, и поперечные силы, направленные по радиусам кривизны срединной поверхности в этих центрах.

Обозначим S - силу, действующую на единицу длины параллельного круга kBl серединной поверхности грани adeh и на всю толщину стенки, нормально к этой грани. Условимся, считать силу положительной, если она производит растяжение, отрицательной в случае сжатия; Т - силу, действующую на единицу длины меридиана kEn и на всю толщину стенки, нормально к боковым граням abcd и efgh. Для знака Т примем то же условие, что и для S.

Силу S назовем меридиональной силой, а Т - кольцевой силой. Очевидно, S лежит в плоскости меридиана, а T - в плоскости параллельного круга.

K - изгибающий момент, действующий на единицу длины меридиана и на всю толщину стенки, стремящийся повернуть элемент вокруг меридиана (кольцевой момент). Будем считать K положительным, если он стремится изогнуть оболочку наружу, и изобразим его вектором, расположенным на оси вращения, направление которого связано с направлением момента правилом правого винта.

М – изгибающий момент, действующий на единицу длины параллельного круга и на всю толщину стенки, стремящийся повернуть элемент вокруг касательной к параллельному кругу (меридиональный момент). Примем для знака М и его изображения те же условия, что и для К.

N - поперечная сила (среза), действующая на единицу длины параллельного круга и на всю толщину стенки, лежащая в плоскости сечений, нормальных к меридиану. По соображениям, изложенным выше, сила N может действовать лишь на нижней и верхней гранях элемента и будет направлена вдоль радиусов кривизны оболочки.

Далее из центра P элемента проведем систему прямоугольных координат x,y,z так, чтобы ось x была направлена по касательной к меридиану, в сторону возрастающих углов ; ось y - по касательной к параллельному кругу в точке P, в сторону возрастающих углов ; ось z - по нормали к срединной поверхности, в сторону центров кривизны.

Условимся силу N считать положительной, если она направлена в сторону положительных z, и действует на элемент, внешняя нормаль которого направлена в сторону положительных x, или если она направлена по z – и действует на элемент, внешняя нормаль которого направлена по x.

Так как мы приняли, что внешние силы, действующие на оболочку, распределены по ее поверхности непрерывно и симметричны относительно оси оболочки, то вследствие симметрии все нагрузки лежат в плоскости (xz). Обозначим через X и Z составляющие внешних сил на единицу поверхности в направлении осей x и z соответственно.

Тогда на грани оболочки действуют следующие силы и моменты:

на грани abcd и efgh сила T R₁ d и момент K R₁ d;

на грань adeh силы S r d = S R₂ sin d; N r d = N R₂ sin d;

и момент M r d = M R₂ sin d;

На грань bcfg сила

S R₂ sin d + d(S R₂  d) = S R₂ sind + d(S R₂ sin) d d/d =

= S R₂ sin d + (S R₂ sin)` d d

и аналогично момент

M R₂ sin d + (M R₂ sin)` d d

и сила

N R₂ sin d + (N R₂ sin)` d d;

на площадку klmh серединной поверхности действуют внешние силы вдоль осей x и y

X dF = X r d R₁ d = X R₁ R₂ sin d d

Z dF = Z r d R₁ d = Z R₁ R₂ sin d d .

Теперь рассмотрим условие равновесия выделенного элемента, для этого необходимо, чтобы сумма проекций внешних и внутренних сил была равна нулю.

2.2.3 Сумма проекций всех сил на ось x.

В направлении оси x действуют внутренние силы S, S + dS, N, N + dN и T. Для нахождения проекций меридиональных и поперечных сил на ось x сделаем сечение в плоскости xz с серединной поверхностью, и покажем, как направлены эти силы.

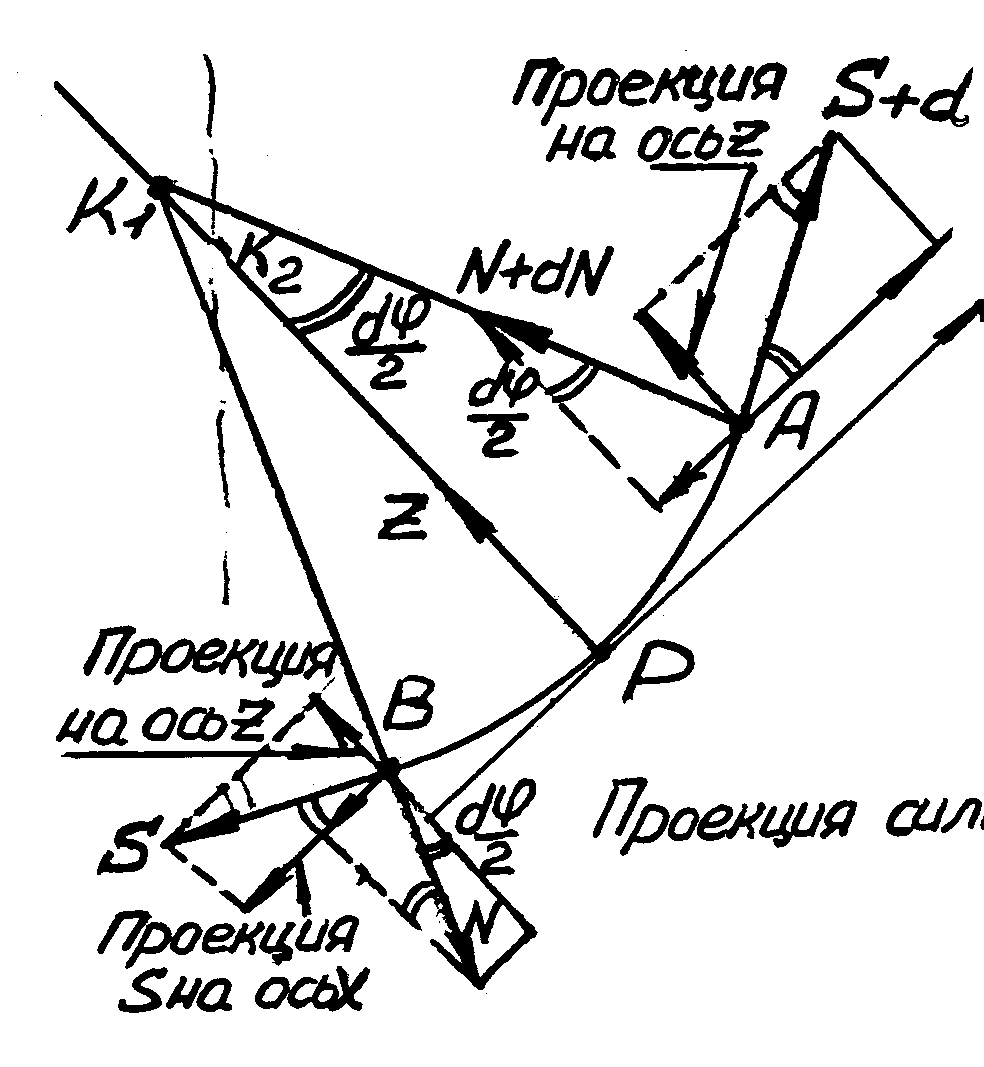
Рисунок 2.3 - Проекции меридиональных и поперечных сил на оси z и x.

Проекции меридиональных сил на ось x равны:

– SR₂sindcos(d/2) + [SR₂sind + (SR₂sin)` dd] cos(d/2) =

= (SR₂sin)` dd cos(d/2).

Без особой погрешности можно принять cos(d/2)  1, как весьма малый угол. Тогда сумма проекций меридиональных сил на ось x равна:

(SR₂sin)` dd.

Проекции поперечных сил на ось x из рис.2.3 имеем:

– NR₂sindsi (d/2) – [NR₂sind + (NR₂sin)` dd] sin(d/2).

Если пренебречь силами порядка малости выше второго и учесть, что sin(d/2)  d/2, то получим сумму проекции от поперечных сил на ось x:

– NR₂ sindd. (2.1)

Спроектируем на ось x кольцевую силу T. Выделим из элемента оболочки серединную поверхность и приложим к ней силу Т.

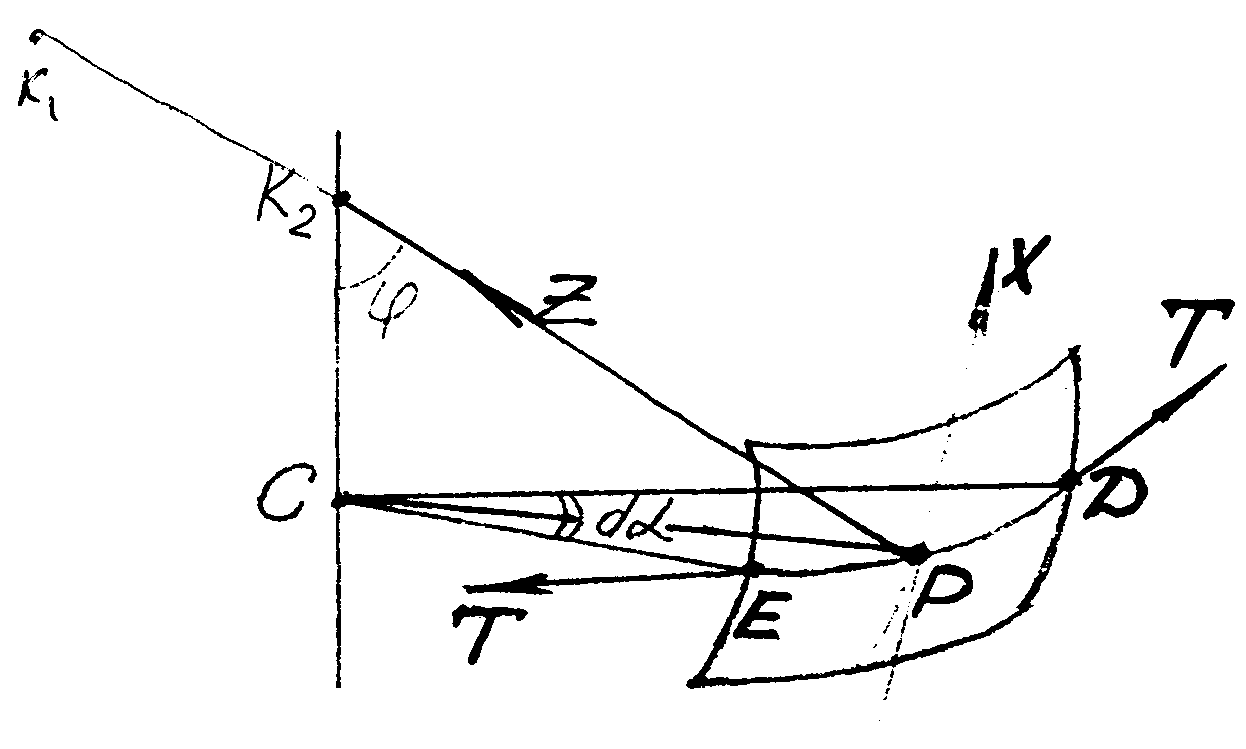
Рисунок 2.4 – Серединная поверхность с кольцевой силой.

Д ля получения проекций на ось x найдем вначале проекцию этих сил на радиус параллельного круга CP, а затем эту проекцию на ось x. Выделим из рис.2.4 сечение в плоскости параллельного круга (рис.2.5).

Рисунок 2.5 – Сечение в плоскости параллельного круга.

Из рис 2.5, проекция от силы T на радиус параллельного круга равна:

2Т R₁ d sin(d/2) = T R₁ d d.

Сделаем из рис. 2.4 сечение в плоскости xz (рис.2.6).

Р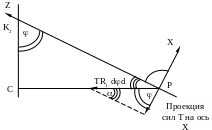 исунок 2.6 - Сечение в плоскости xz.

Тогда проекция от кольцевой силы Т на ось x равна:

– T R₁ d d cos

Для равновесия вдоль оси x должно быть:

(S R₂ sin)` d d – N R₂ sin d d – T R₁ d d +X R₁ R₂ sin d d = 0,

либо:

(S R₂ sin)` – N R₂ sin – T R₁ cos + X R₁ R₂ sin = 0

2.2.4 Сумма проекций всех сил на ось z.

Равнодействующая поперечных сил на ось z из рис.2.3 равна:

– N R₂ sin d cos(d/2) + [N R₂ sin d+ (N R₂ sin)` d d]  cos(d/2) =

= (N R₂ sin)` d d

Равнодействующая меридиональных сил из рис.2.3 равна:

S R₂ sin d sin(d /2) + [S R₂ sin d + (S R₂ sin)` d d] sin(d/2)

Пренебрегая силам и порядка малости выше второго, имеем суммарную проекцию от меридиональных сил на ось z:

S  R₂  sin  d  d

Проекцию кольцевой силы Т на ось z получим аналогично, как и на ось x, т.е. проектируем вначале на радиус параллельного круга (и из рис 2.5 она равна TR₁dd), а затем на ось z.

Р исунок 2.7 - Сечение в плоскости xz.

Из рис. 2.7 имеем проекцию кольцевой силы T на ось z:

T R₁ d d sin.

Сумма проекций всех сил на ось z равна:

(N R₂sin)` d d + S R₂sind d +T R₁d dsin +

+ X R₁ R₂ sin d d + Z R₁ R₂ sin d d = 0,

либо

(N R₂ sin)` + S R₂ sin + T R₁sin + X R₁ R₂ sin + Z R₁R₂ cos = 0.