§ 3.Задачи

Рассмотрим на практическом примере, как можно упростить решение задачи, используя изложенные выше свойства.

Задача 1

В треугольнике АВС сторона АС=15 см. В треугольник вписана окружность. Вторая окружность касается первой и сторон АВ и ВС. На стороне АВ выбрана точка F, а на стороне ВС - точка М так, что отрезок FM является общей касательной к окружностям. Найдите отношение площадей треугольника BFM и четырехугольника АFМС, если FM - 4 см, а точка М отстоит от центра одной окружности на расстояние в два раза большее, чем от центра другой.

Дано: FM-общая касательная AC=15см FM=4см O₂M=2О₁M

Найти S_BFM/S_AFMC

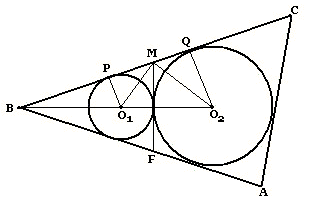
Решение:

1)FM=2√Rr,O₁M/O₂M=√r/R

2)2√Rr=4, √r/R=0,5 →r=1,R=4; PQ=FM=4

3)▲BO₁P и ▲BO₂Q подобны → BP/BQ=O₁P/O₂Q, BP/(BP+PQ)=r/R,BP/(BP+4)=0,25;BP=4/3

4)FM+BP=16/3, S_FBM=r*Р_FBM=1*(16/3)=16/3; AC+BQ=15+4/3+4=61/3

5)S_ABC=R*Р_ABC=4*(61/3)=244/3 → S_BFM/S_AFMC=(16/3):(244/3)=4/61

З адача 2

В равнобедренный треугольник АВС вписаны две касающиеся окружности с их общей точкой Д и проходящей через эту точку общей касательной FK. Найти расстояние между центрами этих окружностей, если основание треугольника АС = 9 см, а отрезок боковой стороны треугольника заключенный между точками касания окружностей равен 4 см.

Дано: ABC – равнобедренный треугольник; FK – общая касательная вписанных окружностей. АС = 9 см; NE = 4 см

Решение:

Т.к. AFKC – равнобедренная трапеция, в которую вписана окружность, то ее высота равна среднему геометрическому ее оснований, т.е. (см) .

Тогда радиус большой окружности равен 3см. Но , следовательно , тогда (см).

А расстояние между центрами окружностей в данной задаче равно (см).

Ответ: см.

З адача 3

Окружности различных радиусов r и R с центрами О₁ и О₂ соответственно касаются внешним образом в точке К. Прямая касается этих окружностей в различных точках

А и В, а вторая прямая – в точках D и C соответственно. Докажите, что ABCD – описанная трапеция и найдите ее высоту.

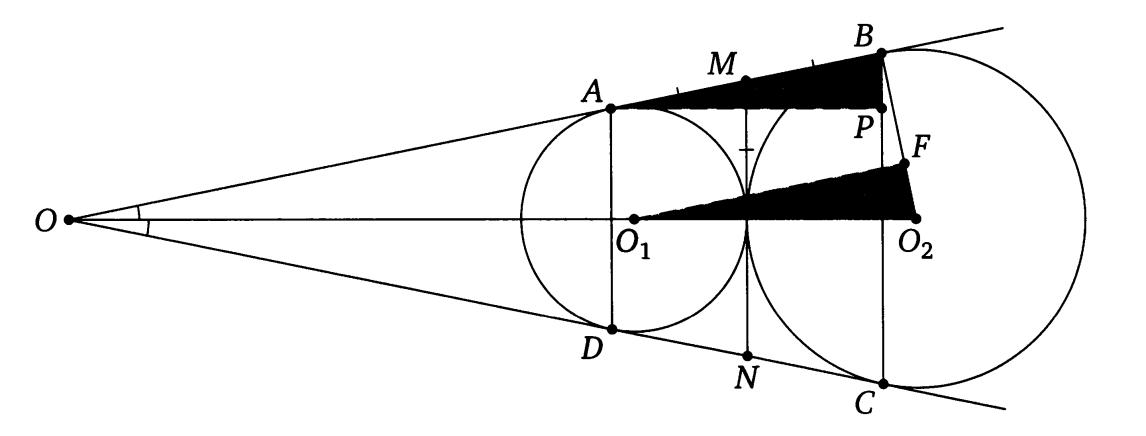
Решение:

Пусть прямые AB и CD пересекаются в точке О. Тогда ОА = ОD, ОВ = ОС, поэтому CD = = AB = 2√Rr

Точки О₁ и О₂ лежат на биссектрисе угла AOD. Биссектриса равнобедренного треугольника AOD является его высотой, поэтому AD ┴ O₁O₂ и BC ┴ O₁O₂ , значит,

AD ║ BC и ABCD – равнобедренная трапеция.

Отрезок MN – ее средняя линия, поэтому AD + BC = 2MN = 2AB = AB + CD

Следовательно, в эту трапецию можно вписать окружность.

Пусть AP – высота трапеции, прямоугольные треугольники АРВ и О₁FO₂ подобны, поэтому АР/О₁F = АВ/О₁О₂.

Отсюда находим, что

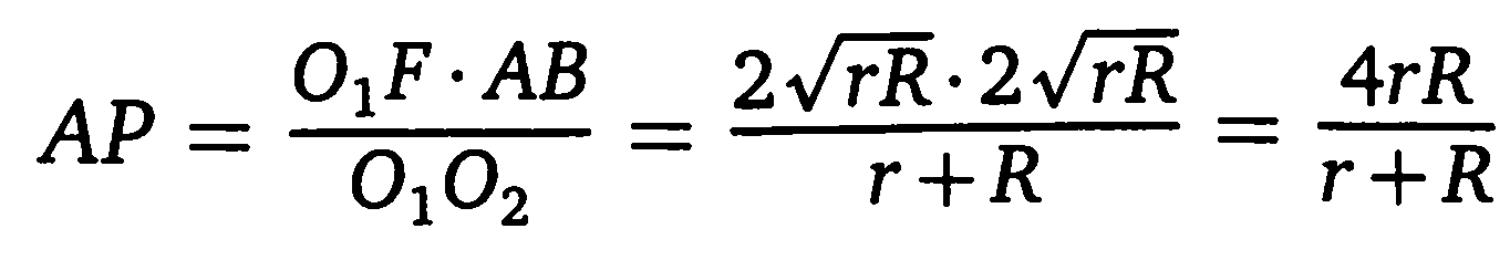
Список литературы

• Приложение к газете «Первое сентября» «Математика» №43, 2003 год

• ЕГЭ 2010. Математика. Задача С4. Гордин Р.К.

14