Министерство образования и науки Российской Федерации

Муниципальное бюджетное общеобразовательное учреждение

города Новосибирска «Гимназия №4»

секция: математика

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

по теме:

СВОЙСТВА ДВУХ КАСАЮЩИХСЯ ОКРУЖНОСТЕЙ

Учеников 10 класса:

Хазиахметова Радика Ильдаровича

Зубарева Евгения Владимировича

Руководитель:

Л.Л. Баринова

учитель математики

высшей квалификационной категории

2010

Содержание

§ 1.Введение………..………………………….…………………………………………………3

§ 1.1 Взаимное расположение двух окружностей………………………...…………...………3

§ 2 Свойства и их доказательства………………………………………..…………….....….…4

§ 2.1 Свойство 1………………...……………………………………..…………………...….…4

§ 2.2 Свойство 2……………………………………………………..…………………...………5

§ 2.3 Свойство 3……………………………………………………..…………………...………6

§ 2.4 Свойство 4……………………………………………………..…………………...………6

§ 2.5 Свойство 5…………………………………..……………………………………...………8

§ 2.6 Свойство 6………………………………………………..………………………...………9

§ 3 Задачи…………………………………………………..…………………...…...………..…11

Список литературы………………………………………………………………….………….13

§ 1.Введение

Многие задачи, включающие в себя две касающиеся окружности, можно решить более коротко и просто, зная некоторые свойства, которые будут представлены дальше.

§ 1.1 Взаимное расположение двух окружностей

Для начала оговорим возможное взаимное расположение двух окружностей. Может быть 4 различных случая.

1.Окружности могут не пересекаться.

2.Пересекаться.

3. Касаться в одной точке снаружи.

4.Касаться в одной точке внутри.

§ 2. Свойства и их доказательства

Перейдем непосредственно к доказательству свойств.

§ 2.1 Свойство 1

Отрезки между точками пересечения касательных с окружностями равны между собой и равны двум средним геометрическим радиусов данных окружностей.

Дано О₁ и О₂ – центры касающихся в точке С окружностей. Их радиусы r и R соответственно.

Из точки P выходят общие касательные окружностей. М и N – точки пересечения внутренней касательной с внешними.

Доказать A₁B₁ = A₂B₂ = 2√Rr

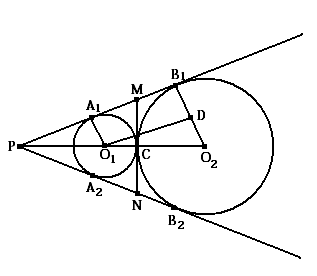
Доказательство 1. О₁А₁ и О₂В₁ – радиусы, проведённые в точки касания.

2. О₁А₁ ┴ А₁В₁, О2В1 ┴ А₁В₁ → О₁А₁ ║ О₂В₁.(по пункту 1)

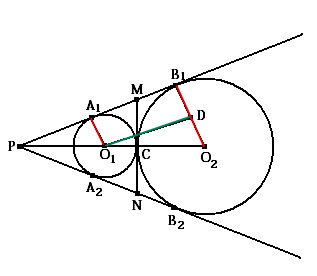
3. ▲О₁О₂D – прямоугольный, т.к. О₂D ┴ О₂В₁

4. О₁О₂ = R + r, О₂D = R – r

3. По теореме Пифагора А₁В₁ = 2√Rr

(O₁D₂=(R+r)²-(R-r)²=R²+2Rr+r2-R²+2Rr-r²=√4Rr=2√Rr)

А₂В₂ = 2√Rr (доказывается аналогично)

Утверждения, используемые в доказательстве 1)Проведем радиусы в точки пересечения касательных с окружностями.

2)Эти радиусы будут перпендикулярны касательным и параллельны друг другу.

3)Опустим перпендикуляр из центра меньшей окружности к радиусу большей окружности.

4)Гипотенуза полученного прямоугольного треугольника равна сумме радиусов окружностей. Катет равен их разности.

5)По теореме Пифагора получаем искомое соотношение.

§ 2.2 Свойство 2

Точки пересечения прямой, пересекающей точку касания окружностей и не лежащей ни в одной из них, с касательными делят пополам отрезки внешних касательных, ограниченные точками касания, на части, каждая из которых равна среднему геометрическому радиусов данных окружностей.

Дано О₁ и О₂ – центры касающихся в точке С окружностей. Их радиусы r и R соответственно.

Из точки P выходят общие касательные окружностей. М и N – точки пересечения внутренней касательной с внешними.

Доказать A₁M = MB₁ = A₂N = NB₂ =√Rr

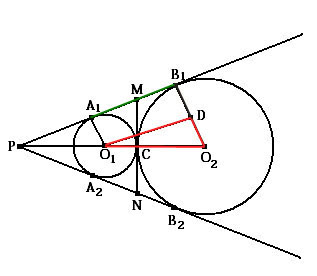
Доказательство 1.МС = МА₁ (как отрезки касательных)

2.МС = МВ₁ (как отрезки касательных)

3.А₁М = МВ₁ = √Rr , А₂N = NB₂ = √Rr (по пункту 1 и 2)

Утверждения, используемые в доказательстве Отрезки касательных, проведенных из одной точки к некоторой окружности равны. Используем это свойство для обеих данных окружностей.

§ 2.3 Свойство 3

Длина отрезка внутренней касательной, заключенного между внешними касательными, равна длине отрезка внешней касательной между точками касания и равна двум средним геометрическим радиусов данных окружностей.

Дано О₁ и О₂ – центры касающихся в точке С окружностей. Их радиусы r и R соответственно.

Из точки P выходят общие касательные окружностей. М и N – точки пересечения внутренней касательной с внешними.

Доказать MN = A₁B₁ =2√Rr

Доказательство Этот вывод следует из предыдущего свойства.

MN = MC + CN = 2MC = 2A₁M = A₁B₁ = 2√Rr

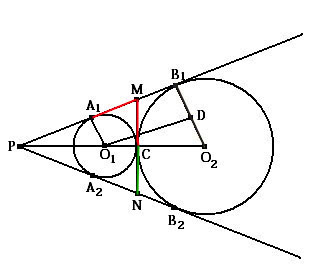
§ 2.4 Свойство 4

Треугольник, образованный центрами касающихся окружностей и серединой отрезка касательной между радиусами, проведенными в точки касания, прямоугольный. Отношение его катетов равно частному корней радиусов этих окружностей.

Дано О₁ и О₂ – центры касающихся в точке С окружностей. Их радиусы r и R соответственно.

Проведены общие касательные окружностей. М и N – точки пересечения внутренней касательной с внешними.

Доказать О₁М / МО₂ = О₁С / МС = r / √Rr = √r / R

O₁МО₂ – прямоугольный треугольник.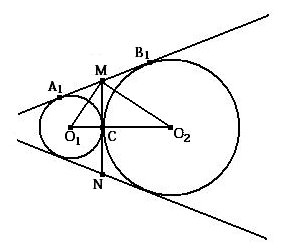

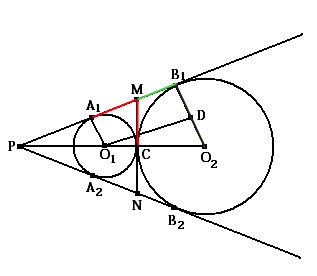
Доказательство 1.МО₁ – биссектриса угла А₁МС, МО₂ – биссектриса угла В₁МС, т.к. центр окружности, вписанной в угол лежит на биссектрисе этого угла.

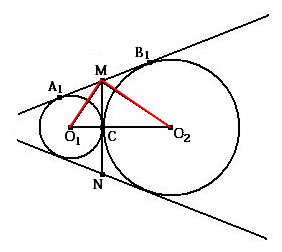
2.По пункту 1 ÐО₁МС + ÐСМО₂ = 0,5(ÐА1МС + ÐСМВ₁) = 0,5p = p/2

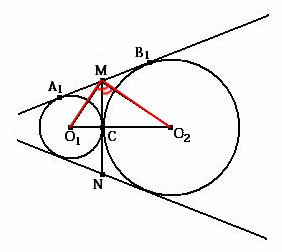
3.ÐО₁МО₂ – прямой. МС – высота треугольника O₁МО₂, т.к. касательная МN перпендикулярна радиусам, проведённым в точки касания → треугольники О₁МС и МО₂С – подобны.

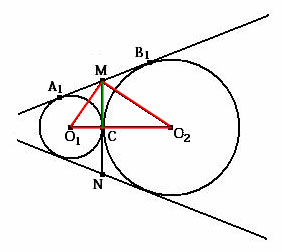
4.О₁М / МО₂ = О₁С / МС = r / √Rr = √r / R (по подобию)

Утверждения, используемые в доказательстве 1)Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. Катеты треугольника являются биссектрисами углов.

2)Пользуясь тем, что образованные таким образом углы равны, получаем, что искомый рассматриваемый нами угол прямой. Делаем вывод о том, что данный треугольник действительно прямоугольный.

3)Доказываем подобие треугольников, на которые высота (так как касательная перпендикулярна радиусам, проведенным в точки касания) делит прямоугольный треугольник, и по подобию получаем искомое отношение.