2. Програмування

Математичне або оптимальне програмування розробляє теорію та методи вирішення умовних екстремальних задач і є основою формального апарату аналізу різноманітних задач управління, планування та проектування. Особливо велику роль відіграє програмування в задачах оптимізації планування суспільного господарства та управління виробництвом. Завдання планування економіки здебільшого зводяться до вибору сукупності чисел (параметрів управління), які забезпечують оптимум деякої функції при обмеженості умов роботи системи.

Залежно від властивостей функцій, які визначають показник якості та обмеження задачі, математичне програмування поділяється на лінійне та нелінійне.

Задачі, в яких цільова функція є лінійною, а умови записуються у вигляді лінійних рівностей та нерівностей, становлять предмет лінійного програмування. Задачі, в яких показник якості рішення або деякі із функцій, що визначають обмеження нелінійні, належать до нелінійного програмування.

Метод лінійного програмування найбільш розповсюджений у прикладних економічних дослідженнях завдяки його достатній наочності, зрозумілості інтерпретацій. Це дає змогу суб'єкту господарювання прийняти найкраще обґрунтоване (за формальними ознаками) рішення в умовах більш-менш жорстких обмежень стосовно доступних для підприємства ресурсів. Особливо ефективне застосування лінійного програмування в аналізі фінансово-господарської діяльності для вирішення насамперед завдань щодо планування діяльності для пошуку оптимальних параметрів випуску та найкращого використання наявних ресурсів.

Отже, сутність методу лінійного програмування полягає у пошуку максимуму чи мінімуму обраної відповідно до мети аналізу цільової функції за наявних обмежень.

Модель (лат. modulus – міра, зразок) – абстрактний образ, який відображає основні риси описуваного явища. Оскільки модель відтворює сутність відповідного об'єкта, вона відтворює й об'єкт, відволікаючись при цьому від другорядних властивостей, які реально властиві досліджуваному об'єкту. Тому модель ніколи повністю не є адекватною об'єкту і передбачає використання процедур абстрагування та ідеалізації.

Терміном "модель" позначають також аналог досліджуваного процесу, предмета чи явища, що відображає суттєві функції та характеристики об'єкта, який моделюється, з погляду мети дослідження.

Під економіко-математичною моделлю слід розуміти математичний опис досліджуваного економічного процесу чи об'єкта. Здебільшого математична модель будь-якого процесу в економіці характеризується за допомогою системи рівностей та нерівностей, які містять певний набір параметрів і змінних величин. Процедура економіко-математичного моделювання замінює дорогі та трудомісткі натуральні експерименти розрахунками.

Проведення економіко-математичного моделювання передбачає 3 основні етапи:

1) постановка мети і визначення завдань дослідження, якісний опис об'єкта у вигляді економічної моделі;

2) формування математичної моделі досліджуваного об'єкта, вибір чи розробка методів дослідження, програмування моделі на ЕОМ, підготовка вихідної інформації;

3) аналіз математичної моделі, здійснення розрахунків, обробка та аналіз отриманих результатів.

ПРИКЛАД. Для виготовлення двох видів кондитерської продукції – печива та цукерок – використовують чотири види сировини: наповнювач, цукор, какао-порошок, муку. Запаси та кількість сировини, яка витрачається кондитерським цехом на виготовлення однієї тонни виробів наведені в табл. 13.2.

Прибуток, який отримують з 1 т печива дорівнює 750 грн, а з тонни цукерок – 1200 грн.

Визначити оптимальні річні обсяги виробництва печива і цукерок, щоб прибуток від їх реалізації був максимальний за наявних ресурсів.

Таблиця 13.2. Ресурси та витрати на виготовлення продукції кондитерського цеху

Вид сировини	Запас сировини, т	Кількість сировини, яка витрачається на виготовлення 1 т продукції, т
		печиво	цукерки
Наповнювач	180	0,1	0,3
Цукор	160	0,2	0,1
Какао-порошок	50	—	0,1
Мука	210	0,3	—

Розв'язання

1. Складемо економіко-математичну модель задачі. Для цього позначимо обсяг виробництва печива як х1% а цукерок як х2. Для їх виготовлення потрібно буде:

– наповнювача: 0,1х₁ + 0,3х₂;

– цукру: 0,2х₁ + 0,1х₂;

– какао-порошку: 0,1х₂;

– муки: 0,3х₁.

Оскільки споживання сировини не повинно перевищувати її запаси, відповідно: 180,160, 50 і 210 т, то зв'язок між використанням сировини та її запасами відобразить система нерівностей:

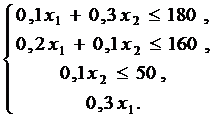
За змістом задачі змінні величини х₁³ 0, х₂³0.

2. Загальний прибуток (П) становитиме 1500 х₁ грн від реалізації печива та 2500 х₂ грн від реалізації цукерок, тобто

П = 750х₁ +1200х₂ max.

3. Розрахуємо х₁ та х₂.

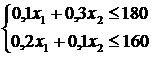 p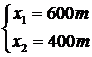 

Таким чином, оптимальний річний обсяг виробництва для отримання максимального прибутку становить для печива – 600 т, цукерок – 400 т. За таких умов очікується одержання прибутку розміром 930 тис. грн:

 (тис. грн).

Аналіз чутливості

Аналіз чутливості дає змогу враховувати мінливість умов виробництва, переробки, реалізації та постачання продукції, кон'юнктуру ринку праці. Він незамінний при плануванні виробничої діяльності, аналізі інвестиційних проектів, при прогнозуванні чистого прибутку підприємства в умовах невизначеності, зміні цін, ринкових попиту і пропозиції.

Аналіз чутливості передбачає дослідження залежності результативного показника (найчастіше чистої теперішньої вартості та внутрішньої норми дохідності) від варіації значень показників, що беруть участь у його визначенні (ключових перемінних).

Він дає змогу визначити силу реакції результативного фактора на зміну факторних ознак і відповісти на запитання, що буде з результативним показником, якщо зміниться значення деякої вихідної величини? Виходячи з цього, його ще називають аналізом "що буде, якщо". В основу аналізу чутливості покладено поетапну зміну вихідного показника за незмінності інших показників.

Аналіз чутливості здійснюється у кілька етапів:

1) встановлення формального зв'язку у вигляді математичного рівняння або нерівності між результативним та формуючими його вихідними показниками;

2) визначення найбільш ймовірних значень для вихідних показників та можливий розмах їх змін (варіацій);

3) дослідження впливу зміни значень вихідних показників на кінцевий результат.

Проект із меншою чутливістю результативного показника вважається менш ризиковим.

Розглянемо застосування аналізу чутливості на прикладі промислового підприємства.

ПРИКЛАД. Виробниче підприємство "Смак" спеціалізується на випуску вареників. Для розробки плану роботи на наступний квартал зробити аналіз чутливості прибутку до змін основних його параметрів. При цьому планові змінні витрати на 1 кг готової продукції підприємства (z) дорівнюють 6 грн. Постійні витрати за квартал (FC) становитимуть 8000 грн. Відпускна ціна вареників (р) планується на рівні 11,5 грн. Точка беззбитковості дорівнює

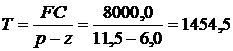 кг.

Розрахований вище обсяг виробництва дасть змогу покрити всі витрати і вийти на нульовий прибуток. Якщо ж підприємство буде виробляти менше продукції, тоді матимуть місце збитки і діяльність виявиться збитковою.

Вивчивши стан ринку, підприємство "Смак" запланувало випуск вареників (q) на наступний квартал обсягом 2000 кг. За такого обсягу виробництва рівень прибутку (П) становитиме:

грн.

Скориставшись аналізом чутливості розглянемо чутливість прибутку до зміни основних параметрів на 1%.

1. Припустимо, що змінні витрати на 1 кг продукції збільшилися на 1%, тобто:

z¹=1,01z.

Визначимо, яким буде прибуток при вказаному вище обсязі випуску продукції:

грн.

.

Як бачимо, зростання змінних витрат на 1% спричинило зниження прибутку на 4%. Аналогічно можна розрахувати, що зменшення цих витрат на 1% супроводжуватиметься збільшенням прибутку на 4%.

2. Припустимо, що постійні витрати збільшилися на 1%. Тоді прибуток буде:

 грн.

.

Отже, при збільшенні постійних витрат на 1% слід очікувати зменшення прибутку на 2,7%.

3. Розглянемо випадок збільшення ціни на 1%.

 грн.

.

Це означає, що при плановому обсязі випуску продукції збільшення ціни реалізації на 1% супроводжуватиметься зростанням прибутку на 7,7%.

4. Покажемо як зміниться прибуток за умови збільшення обсягу виробництва на 1% порівняно з планом:

 грн.

.

Таким чином, результати зробленого аналізу чутливості показують, що прибуток підприємства "Смак" найбільш чутливий до зміни ціни (збільшення або зменшення ціни реалізації на 1% призводить до зростання чи падіння прибутку на 7,7%). Далі за ступенем впливу на рівень прибутку йдуть питомі змінні витрати (±4% у відповідь на зміну на 1% г) та обсяг виробництва (±3,7%). Найменший вплив на прибуток підприємства "Смак" має зміна постійних витрат (однопроцентне коливання їх рівня призводить до зміни величини прибутку на 2,7%).

Враховуючи найвищу чутливість прибутку до зміни ціни, керівництву підприємства необхідно приділити максимум уваги питанням ціноутворення та збутовій політиці, оскільки це дає найбільший економічний ефект.

Тим часом слід пам'ятати і про те, що висока чутливість прибутку до зміни ціни може негативно позначитися на фінансовому стані підприємства у випадку несприятливої кон'юнктури ринку і зниження ринкових цін. Особливо це небезпечно у роздрібній торгівлі та виробництві продуктів харчування, які належать до висококонкурентних галузей. Саме ці галузі найбільше залежать від цін, які встановляються на ринку під впливом попиту і пропозиції, що обмежує можливості підприємства щодо її регулювання. В цьому випадку резерви підвищення прибутковості слід шукати в зниженні витрат або збільшенні випуску продукції.

Вивчення чутливості здійснюється також за допомогою методу сценаріїв, який дає змогу поєднувати дослідження чутливості результативного показника з аналізом імовірнісних оцінок його відхилень.

Проведення аналізу чутливості за методом сценаріїв передбачає проходження таких етапів:

1) визначення кількох варіантів змін ключових перемінних (песимістичний, найбільш ймовірний та оптимістичний);

2) присвоєння ймовірної оцінки кожному варіанту змін;

3) розрахунок ймовірного значення обраного критерію та оцінка його відхилень від середнього рівня для кожного варіанта;

4) аналіз ймовірного розподілу одержаних результатів.

Той проект чи варіант, який має найменші стандартні відхилення вважається менш ризиковим.

 Метод Монте-Карло

Поєднання аналізу чутливості та методу сценаріїв на основі теорії ймовірностей здійснюється в імітаційному моделюванні за методом Монте-Карло.

Метод Монте-Карло – це чисельний метод, основу якого становить одержання великого числа реалізацій випадкового процесу, який формується так, щоб імовірнісні характеристики (математичні очікування, імовірність деяких подій, імовірність попадання траєкторії процесу в деяку область тощо) дорівнювали певним величинам задачі, яка розв'язується.

Метод Монте-Карло ґрунтується на імітації масового процесу шляхом вирахування його ходу, в якому випадкові коливання визначаються за допомогою жеребка або таблиці випадкових чисел. Економічний експеримент може замінюватися статистичними випробуваннями моделі економічного процесу. Побудова цієї моделі може ґрунтуватися на розподілі випадкових величин у досліджуваному процесі.

Таким чином, сутність методу Монте-Карло полягає в тому, що замість аналітичного описання системи масового обслуговування здійснюється "розіграш" випадкового процесу, який відбувається в системі масового обслуговування, шляхом спеціально організованої процедури. В результаті такого "розіграшу" здійснюється кожного разу нова, відмінна від інших реалізація випадкового процесу. Цю множину реалізацій можна використати як деякий штучно отриманий статистичний матеріал, що обробляється звичайними методами математичної статистики. Після такої обробки можуть бути отримані майже будь-які характеристики обслуговування.

Етапи імітаційного моделювання за методом Монте-Карло

Перший етап імітаційного моделювання за методом Монте-Карло. Розробка прогнозної моделі передбачає формування очікуваної імітаційної моделі, яка повинна адекватно відображати майбутній сценарій реалізації проекту.

Другий етап – виявлення чинників ризику включає відбір ключових змінних для моделювання.

Третій етап – визначення умов кореляції полягає у встановленні формальної залежності між результативним показником і відібраними ключовими змінними.

Четвертий етап – імовірнісний розподіл відібраних ключових змінних передбачає здійснення таких кроків:

1) визначення обмежень можливої зміни відібраних ключових змінних;

2) встановлення імовірнісної ваги за межами значень.

П'ятий етап – імітаційне прогнозування вимагає генерування випадкових сценаріїв реалізації проекту з використанням вибраних допущень.

Шостий етап – аналіз отриманих результатів потребує здійснення статистичної оцінки та інтерпретації одержаних результатів імітації.

Імітаційне моделювання за методом Монте-Карло застосовується для побудови математичної моделі для інвестиційного проекту з важкопрогнозованими показниками. Його метою є визначення розподілу результатів реалізації проекту на основі імовірнісного розподілу його ключових змінних і кореляційної залежності між ними.

Особливістю та однією з основних вимог імітаційного моделювання за методом Монте-Карло є застосування спеціальних комп'ютерних програм. Це, зокрема, пояснюється тим, що генерування випадкових сценаріїв реалізації проекту (етап 5) повторюються 500–1000 разів.

Одержані значення результативного показника проекту (чистої теперішньої вартості чи внутрішньої норми дохідності) використовуються для побудови графіка щільності його розподілу зі своїм власним математичним очікуванням і стандартним відхиленням. На основі значення математичного очікування та стандартного відхилення обчислюється коефіцієнт варіації результативного показника проекту, за допомогою якого оцінюється індивідуальний ризик проекту.

Метод Монте-Карло застосовується в розрахунках для складних комплексів, в яких використання класичних методів розрахунків практично неможливе. Він набув поширення у розв'язанні економічних задач, дослідженні функціонування складних систем, наприклад в теорії масового обслуговування, управлінні та нормуванні запасів та ін.

Наприклад, для вирішення питання щодо розширення магазину необхідно проаналізувати черги, які тут виникають. Час підходу покупців і час їх обслуговування мають випадковий характер і їх розподіл може бути встановлений за наявною інформацією. Внаслідок взаємодії цих випадкових процесів створюється черга.

Згідно з методом Монте-Карло перебирають (за допомогою ЕВМ) усі можливі стани системи з різним числом покупців за годину, часом їх обслуговування тощо, зберігаючи ті самі характеристики розподілу. В результаті багаторазового штучного відтворення роботи магазину розраховують характеристики обслуговування так, якби вони були одержані при спостереженні над реальним потоком покупців.

Теорія ігор

Теорія ігор – розділ прикладної математики, який вивчає математичні моделі прийняття рішень у так званих конфліктних ситуаціях, що мають місце. Основоположниками теорії ігор є математик Дж. Фон Непман та економіст О. Моргенштерн. В подальшому її розвинули Неш Джон, Зелтен Райнхард, Харшаньї Джон Чарльз, які в 1994 р. стали лауреатами премії пам'яті Альфреда Нобеля з економіки "за пріоритетний вклад в аналіз некооперативних ігор".

Сутність теорії ігор полягає у встановленні оптимальної (у тому чи іншому змісті) стратегії поведінки в конфліктних ситуаціях. Метою теорії ігор є визначення оптимальної стратегії для кожного гравця.

Стратегією гравця називається сукупність правил, що обумовлюють вибір його дій при кожному особистому ході залежно від наявної ситуації.

Під конфліктом розуміється ситуація, в якій стикаються інтереси двох чи більше сторін, які переслідують різні (інколи протилежні) цілі. Кожна з сторін-учасників конфліктних ситуацій може у певний спосіб впливати на хід подій, але не має змоги повністю ним керувати. Конфліктні ситуації виникають під час вирішення різноманітних економічних проблем (відносини між організаціями-виробниками і споживачами, торгівля, економічна конкуренція тощо).

Щоб дослідити конфліктну ситуацію будують її формалізовану спрощену модель, яка називається грою. Теорія ігор встановлює для різних класів конфліктних ситуацій оптимальні лінії поведінки учасників – стратегії гравців, що забезпечують рівновагу у грі. Оптимальні стратегії гравців гарантують кожному з них якийсь виграш, причому такий, що відхід будь-якого з учасників від узгодженої стратегії може тільки зменшити його виграш.

Ігри різняться за числом учасників, характеристиками так званих платіжних функцій, які визначають виграш кожного гравця залежно від його поведінки і поведінки інших учасників конфлікту, за інформацією про ситуацію, що склалася та яка є в розпорядженні партнерів, за правилами, що обмежують вибір лінії поведінки учасників, за можливостями укладання угод між ними і входження в коаліції, за визначенням поняття "рівноваги" чи "справедливого вирішення гри".

Наприклад, теорія ігор математично описує характерні для ринкової економіки явища конкуренції у вигляді гри. Простий варіант передбачає протистояння двох конкурентів за ринок збуту. Складні варіанти передбачають, що в грі беруть участь багато супротивників, вступаючи при цьому між собою в постійні або в тимчасові союзи. У першому випадку гра називається парною, в другому – гра л-осіб, або множинна. У виразі наявності союзів гра має назву коаліційної.

Складовою теорії ігор виступає статистична теорія ігор. Це розділ сучасної прикладної математики, який вивчає методи обґрунтування оптимальних рішень в конфліктних ситуаціях.

У теорії статистичних ігор наявні такі поняття як вихідна стратегічна гра і власне статистична гра. В цій теорії першого гравця називають природою, вкладаючи в це поняття сукупність обставин, в яких доводиться приймати рішення другому гравцю, якого називають статистиком.

Якщо виграш одного гравця дорівнює програшу іншого, то гра називається антагоністичною або грою з нульовою сумою. У процесі гри її учасники здійснюють ходи. Ходом гравця називається вибір та здійснення однієї із передбачених правилами дій.

Ходи бувають двох видів: особисті та випадкові. Особистий хід – це свідомий вибір гравцем одного з можливих варіантів дій. У подальшому ми будемо розглядати тільки особисті ходи гравців. Випадковий хід – це випадково вибрана дія.

Для того, щоб вирішити гру, або знайти рішення гри необхідно для кожного гравця вибрати стратегію, яка б відповідала умові оптимальності. Це означає, що один із гравців повинен одержати максимальний виграш, у той час як другий дотримується своєї стратегії. Такі стратегії називаються оптимальними.

Оптимальні стратегії мають також відповідати умові стійкості, тобто будь-кому з гравців повинно бути невигідно відмовитися від своєї стратегії у цій грі.

Якщо гра повторюється багато разів, то тоді гравців може цікавити не виграш і програш кожного разу в кожній конкретній партії, а середній виграш (програш) в усіх партіях.

Статистична теорія ігор відрізняється від стратегічної теорії ігор. Так, стратегічна теорія ігор передбачає такі умови:

– активні дії обох гравців;

– обидва гравці поводяться розумно з погляду своїх інтересів;

– повна невизначеність у виборі стратегії кожним гравцем;

– обидва гравці діють на підставі детермінованої інформації, визначеної матрицею втрат.

На відміну від стратегічної статистична теорія ігор відбувається за таких умові:

– природа не є активним гравцем, тобто вона "нерозумна" і не протидіє максимальному виграшу другого гравця;

– статистик (другий гравець) намагається виграти гру в уявного противника, тобто у природи;

– часткова невизначеність у виборі стратегії;

– природа розвивається і діє відповідно до об'єктивно існуючих законів;

– наявність можливості у статистика поступового вивчення законів, зокрема, на основі статистичного експерименту.

ПРИКЛАД. Швейна фабрика випускає жіночі плащі та пальта, реалізація яких здійснюється через фірмовий магазин і залежить від природних кліматичних умов, насамперед від погодних. Основні виробничі показники фабрики наведені в табл. 13.3 з додатково введеними їх буквеними позначеннями.

Визначити оптимальну стратегію реалізації продукції швейної фабрики, яка б сприяла отриманню максимального прибутку.

Розв'язання

1. Визначимо спочатку гравців. У ролі природи (перший гравець) тут виступатиме попит на продукцію. Множину станів природи (стратегії) позначимо

,

де   – попит на продукцію фабрики в теплу погоду;

 – попит на продукцію в прохолодну погоду.

У ролі статистика виступатиме фабрика (другий гравець), яка має два можливі варіанти (стратегії) розвитку подій ,   які означають, що обсяги реалізації продукції залежать від погодних умов – відповідно теплої і прохолодної погоди.

Передбачається, що статистик, який займає активну позицію, може оцінювати наслідки кожного варіанта реалізації продукції залежно від стану природи.

Таблиця 13.3. Основні виробничі показники швейної фабрики за видами продукції за березень – квітень

Вид продукції	Собівартість одиниці, грн (г)	Ціна, грн (р)	Обсяг реалізації, од. (q)
			Тепла погода	Прохолодна погода
Плащі	400	800	2000	1080
Демісезонні пальта	1350	2430	700	1100

2. Функція   буде функцією прибутку. її можна задати аналітичним виразом

.

3. Розглянемо стратегії гравців, зробивши відповідні розрахунки очікуваного прибутку:

– в умовах здійснення стратегії природи ujy що відповідає попиту на продукцію фабрики в теплу погоду, очікуваний прибуток становитиме:

П = 2000(800 - 400) + 700(2430 - 1350) = 1556 (тис. грн);

– взявши за основу стратегію природи v2, що передбачає попит на продукцію в прохолодну погоду, фабрика отримає прибуток:

П = 1080(800 - 400) + 1100(2430 - 1350) = 1620 (тис. грн);

– якщо фабрика прийме стратегію а₁, яка відповідає теплій погоді, тоді їй вдасться продати всі плащі, але тільки частину пальт (700 із 1100 од.) та отримати прибуток:

П= 2000(800 - 400) + 700(2430 - 1350) - (110 - 700)х

х (2430 - 1350) = 1124 (тис. грн);

– коли фабрика обере стратегію а₂, яка відповідає прохолодній погоді, то вона продасть усі пальта і частину плащів (1080 із 2000 од.) і отримає прибуток:

П = 1080(800 - 400) + 1100(2430 - 1350) - (2000 - 1080) х

х (800 - 400) = 1252 (тис. грн).

4. На основі одержаних даних побудуємо платіжну матрицю (матрицю гри) – табл. 13.4.

Таблиця 13.4. Матриця прибутку   фабрики, тис. грн

a v			min за рядками
	1556	1124	1124
	1252	1620	1252
max за стовпцями	1556	1620	—

Із платіжної матриці видно, що перший гравець "природа" ні за яких варіантів розвитку подій не отримає прибуток менший ніж 1124 тис. грн. Проте за збігу погодних умов з обраною стратегією, виграш фабрики становитиме 1556 або 1620 тис. грн. Якщо другий гравець "фабрика" буде постійно застосовувати стратегію  , а гравець природа – стратегію  , то виграш зменшиться до 1252 тис. грн.

Подібна тенденція відбуватиметься, коли гравець "фабрика" буде постійно застосовувати стратегію  , а гравець "природа" – стратегію  .

Отже, можна зробити висновок, що найбільший прибуток фабрика може одержати, якщо буде почергово застосовувати стратегії at та а2. Така стратегія називається змішаною, а її складові (  та  ) – чистими стратегіями.

Оптимізація змішаної стратегії дасть змогу другому гравцю (статистика) – фабриці завжди отримувати середнє значення виграшу незалежно від стратегії першого гравця (природа).

Покажемо це на нашому прикладі. Для цього позначимо частоту застосування фабрикою стратегії   через  . Виходячи з цього, частота застосування ним стратегії   становитиме  .

Якщо фабрика застосує оптимальну змішану стратегію, то і за стратегії   (тепла погода) і за стратегії   (прохолодна погода) другого гравця (природа) вона повинна отримати однаковий середній прибуток:

1556  + 1124(1 -  ) = 1252  + 1620(1 -  );

1556  + 1124 - 1124  - 1252  + 1620 - 1620 ;

800  = 496;

;

.

Справді, при застосуванні стратегії   (тепла погода) гравця природи середній прибуток фабрики дорівнюватиме

1556  + 1124(1 -  ) = 1556 ž 0,62 +1124 ž 0,38 =

= 1391,84 (тис. грн).

При реалізації стратегії v2 (прохолодна погода) гравця природи середній прибуток фабрики становитиме:

1252  + 1620(1 -  ) = 1252 ž 0,62 + 1620 ž 0,38 =

= 1391,84 (тис. грн).

Таким чином, гравець фабрика, застосовуючи чисті стратегії   та   у відношенні 31 до 19 (приблизно 3 до 2), матиме оптимальну змішану стратегію, що забезпечить йому у будь-якому випадку середній прибуток розміром 1391,84 тис. грн, тобто середній платіж дорівнюватиме 1391,84 тис. грн. Такий середній платіж, який одержують при реалізації оптимальної стратегії, називається ціною гри.

Визначимо також кількість пальт і плащів, які фабрика повинна випускати для одержання максимального прибутку:

(2000 плащів + 700 пальт) ž 0,62 + (1080 плащів +

+ 1100 пальт) ž 0,38 = 1240 плащів + 434 пальта +

+ 410,4 плащів + 418 пальт = 1650 плащів + 852 пальта.

Таким чином, оптимальна стратегія фабрики означає 1650 плащів та 852 пальта. За таких умова вона отримає середній прибуток розміром 1391,84 тис. грн.

Ігрові підходи використовуються економістами як на макрорівні при розробці моделей, в яких враховуються інтереси різних ланок економіки, так і на рівні підприємства для вибору оптимальних рішень при створенні запасів сировини, матеріалів, напівфабрикатів, підвищенні якості продукції, маркетинговій діяльності тощо.

Перевагою теорії ігор є можливість розширення поняття оптимальності, включаючи, наприклад, компромісне рішення, яке йде на задоволення різних потреб у грі. З іншого боку, в економічних задачах, аналіз яких зводиться до математичного програмування або до теорії ігор, при елементарній оцінці ефективності варіанта, кількість варіантів настільки велика, що вибрати оптимальний, як правило, вкрай важко.

Значним обмеженням теорії ігор є єдиний показник виграшу як характеристика ефективності, хоча на практиці при вирішенні більшості економічних завдань зустрічаються декілька показників ефективності. Крім того, в економіці здебільшого виникають такі ситуації, коли інтереси партнерів не носять антагоністичного характеру. Це свідчить про необхідність подальшого розвитку апарату теорії ігор відповідно до економічних реалій і виробничої необхідності.

Теорія масового обслуговування

На практиці при вивченні операцій часто доводиться мати справу з системами, призначеними для багаторазового використання при розв'язанні однотипних задач. Процеси, які виникають при цьому отримали назву процесів обслуговування, а системи – систем масового обслуговування. Прикладами таких систем є ремонтні майстерні, телефонні системи, обчислювальні комплекси, магазини тощо.

Кожна система масового обслуговування складається з певного числа обслуговуючих одиниць, зокрема приладів, пристроїв, пунктів, станцій, які називають каналами обслуговування. Каналами можуть виступати продавці, перукарі, обчислювальні машини, точки продажу, лінії зв'язку та ін. За кількістю каналів системи масового обслуговування поділяються на одноканальні (один канал) та багатоканальні (декілька каналів).

Заявки надходять в систему масового обслуговування зазвичай нерегулярно, а випадково, утворюючи так званий випадковий потік заявок (вимог ). Обслуговування заявок триває також якийсь випадковий час. Випадковий потік заявок і часу обслуговування призводить до того, що система масового обслуговування виявляється завантаженою нерівномірно: в якісь періоди часу накопичується дуже велика кількість заявок, а в інші періоди система працює з неповним завантаженням або простоює. Для того, щоб максимально оптимізувати, регулювати ці процеси шляхом прийняття зважених та обґрунтованих управлінських рішень використовується теорія масового обслуговування.

Теорія масового обслуговування – теорія, яка вивчає статистичні закономірності в масових операціях, що складаються з великого числа однорідних елементарних операцій. До них, зокрема належать: складання однотипних деталей на конвеєрі, видача інструментів, ремонт верстатів, робота телефонної станції, обслуговування покупців у магазині, в білетних касах, клієнтів у перукарнях, технічне обслуговування машин та обладнання тощо.

Синонімом теорії обслуговування є теорія черг. У системах масового обслуговування, в яких заявки на елементарні операції надходять у випадкові моменти часу або обслуговуються протягом випадкових проміжків часу, поява черг – неминуче зло. За великої кількості каналів обслуговування (ремонтних бригад, продавців, телефоністок і т. п.) система зазнає збитків через можливі тривалі простої каналів. За малої кількості каналів обслуговування, збитки системи спричиняють черги, які накопичуються.

Завдання теорії масового обслуговування – вивчити статистичні закономірності вхідного потоку заявок на елементарні операції та тривалість обслуговування заявок, а також дати оцінку якості систем обслуговування (з'ясувати пропускну здатність) за різних правил формування черг. Черги можуть бути організовані по різному – з обмеженою та необмеженою довжиною черги, з обмеженим часом очікування та ін.

Предметом теорії масового обслуговування є побудова математичних моделей, які пов'язують задані умови роботи систем масового обслуговування (число каналів, їх продуктивність, характер потоку, заявок тощо) з показниками ефективності цих систем, що описують їх здатність справлятися з потоком заявок.

Під потоком подій розуміють послідовність однорідних подій, які настають одна за другою в якісь випадкові моменти часу (наприклад, потік викликів на телефонній станції, потік відмовлень БВМ, потік покупців тощо).

Потік характеризується інтенсивністю ( ) – частотою появи події або середнім числом подій, які надходять в систему масового обслуговування за одиницю часу.

В ролі показників ефективності систем масового обслуговування можуть використовуватися такі:

– середнє (тут і далі середнє як математичне очікування відповідних випадкових величин) число заявок, які обслуговуються за одиницю часу;

– середня кількість заявок у черзі;

– середній час чекання на обслуговування;

– ймовірність відмови в обслуговуванні без чекання;

– ймовірність того, що число заявок в черзі перевищить певне значення тощо.

Системи масового обслуговування поділяються на два основні типи (класи): з очікуванням (чергою) та з відмовленнями. У системі масового обслуговування з очікуванням заявка, яка надійшла в момент зайнятості каналів, не відправляється, а стає в чергу на обслуговування.

В системах з відмовленням заявка, яка надходить в момент, коли всі канали зайняті, отримує відмовлення та покидає систему, не приймаючи участі в подальшому процесі обслуговування (наприклад, заявка на телефонну розмову в момент, коли всі канали зайняті, отримує відмовлення і залишає систему не обслуженою).

У ролі показників ефективності системи масового обслуговування з відмовленнями застосовуються такі:

1. Абсолютна пропускна здатність (А) – показник, який показує середню кількість заявок, що обслуговуються за одиницю часу. Він розраховується за формулою

,

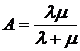де   – інтенсивність потоку заявок;

 – інтенсивність потоку обслуговування.

При цьому інтенсивність потоку обслуговування є оберненою величиною до середнього часу обслуговування ( ):

.

2. Відносна пропускна здатність (Q) – показник, що характеризує середню частку заявок, яка надійшла та обслуговується системою. Обчислюється за формулою

.

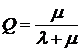3. Ймовірність відмови (Р_від) – величина, яка характеризує ймовірність того, що заявка залишить систему масового обслуговування не обслуженою. Показує частку заявок, яким буде відмовлено в наданні відповідної послуги.

.

4. Середнє число зайнятих каналів ( ) (для багатоканальної системи). Цей показник розраховується у такий спосіб:

.

Визначається також інтенсивність навантаження каналу – р (або приведена інтенсивність потоку заявок) – це показник, який виражає середню кількість заявок, яка надходить за середній час обслуговування однієї заявки. Він розраховується за формулою

.

В багатоканальних системах масового обслуговування з граничними ймовірностями використовують формули для граничних ймовірностей стану, які отримали назву формул Ерланга на честь А.К. Ерланга (кінець XIX – початок XX ст.) – датського інженера, математика, засновника теорії масового обслуговування.

Ймовірність відмови системи масового обслуговування – це гранична ймовірність того, що всі п каналів системи будуть зайняті, тобто:

;

;

,  , …,  , …,  .

Відносна пропускна здатність – ймовірність того, що заявка буде обслужена визначається:

.

Абсолютна пропускна здатність розраховується:

.

Для класифікації систем масового обслуговування важливе значення має дисципліна обслуговування, яка визначає порядок вибору заявок з числа тих, що надійшли, та порядок розподілу їх між вільними каналами. За цією ознакою обслуговування заявки може бути організовано за принципами черговості надходження: в порядку надходження (з початку) або навпаки обслуговуються ті, які надійшли в кінці (з кінця), з пріоритетом обслуговування (в першу чергу обслуговуються найважливіші заявки).

ПРИКЛАД. Заявки на телефонні переговори на переговорному пункті надходять з інтенсивністю  , яка дорівнює 80 заявок на годину, а середня тривалість розмови по телефону  .

1. Визначити показники ефективності роботи системи масового обслуговування (переговорного пункту) за наявності одного телефонного номера.

2. Визначити оптимальну кількість телефонних номерів на переговорному пункті, якщо умовою оптимальності вважати

задоволення в середньому з кожних 100 заявок не менше 80 заявок на переговори.

Розв'язання

1. Розрахуємо інтенсивність потоку обслуговування:

.

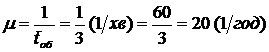2. Визначимо відносну пропускну здатність системи масового обслуговування:

.

Це означає, що в середньому тільки 20% заявок, які надходять, будуть задоволені й за ними будуть надані послуги, тобто здійсняться переговори по телефону.

3. Ймовірність відмови в обслуговуванні ( ) становитиме:

.

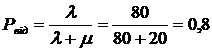Отже, в середньому 80% заявок, які надійдуть на переговори, отримають відмову в обслуговуванні.

4. Абсолютна пропускна здатність системи масового обслуговування – переговорного пункту дорівнюватиме

.

Таким чином, в середньому за годину будуть обслужені 16 заявок на переговори.

З цього можна зробити висновок, що за наявності тільки одного телефонного номера переговорний пункт буде погано справлятися з потоком заявок.

Для виконання другого завдання задачі – визначення оптимального числа номерів на телефонній станції, слід перш за все проаналізувати інтенсивність навантаження каналу.

5. Обчислимо інтенсивність навантаження каналу:

.

Тобто, за час середньої за тривалістю телефонної розмови  надходить в середньому 4 заявки на переговори.

6. Для одержання характеристик системи (переговорного пункту) та вибору оптимального варіанта кількості номерів слід поступово збільшувати число каналів (телефонних номерів) n = 2,3,4, ..., перетворюючи таким чином наявну систему масового обслуговування з одноканальної в багатоканальну. Тоді відносна пропускна здатність становитиме:

;

;

за  ;  .

Абсолютна пропускна здатність дорівнюватиме:

.

Аналогічно розрахуємо основні характеристики системи масового обслуговування для 3, 4, 5, 6 каналів обслуговування (номерів телефонів) та зведемо їх у табл. 13.5.

Таблиця 13.5. Основні характеристики обслуговування заявок на переговори переговорним пунктом залежно від кількості номерів

Характеристика	Кількість каналів (номерів)
	1	2	3	4
Відносна пропускна здатність (Q)	0,20	0,38	0,80	0,95
Абсолютна пропускна здатність (А)	16,0	30,4	64,0	76,0

Отже, за умовами оптимальності Q³=0,8, тому на переговорному пункті необхідно встановити 3 телефонні номери (в цьому випадку Q = 0,80). Це означає, що за годину будуть обслуговуватися в середньому 64 заявки (А = 64), а середня кількість зайнятих номерів (каналів) дорівнюватиме

.

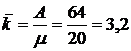Не дивлячись на велике значення теорії ігор для прийняття управлінських рішень, вона не має універсального характеру. Одним із основних обмежень її застосування є те, що в цій грі наявний єдиний показник виграшу як характеристика ефективності. Проте на практиці при вирішенні більшості економічних завдань зустрічаються декілька показників ефективності. Крім того, в економіці здебільшого виникають такі ситуації, коли інтереси партнерів не мають антагоністичного характеру. Ці особливості слід враховувати аналітику при виборі методів дослідження тих чи інших економічних явищ і процесів.