2.4. Необходимое условие локального экстремума.

Такое условие дает хорошо известная из курса математического анализа

Теорема. Если f — дифференцируемая функция и x* — ее локальный минимум, то f (x*) = 0.

Напомним  д о к а з а т е л ь с т в о  теоремы. Допустим противное: f (x*)  Q. Положим x_t = x*  tf (x*) для всех t > 0. Тогда, во-первых, очевидно, x_t  x*   при t  0 и, во-вторых, по определению градиента,

f(xt) = f(x*) + (f (x*), xt  x*) + o(xt  x*) = = f(x*) + (f (x*), tf (x*)) + o(tf (x*)) = = f(x*)     ||f (x*)||2 +  o(tf (x*)) t   .

(6)

Поскольку ||f (x*)|| > 0, а

o(tf (x*)) t

= ||f (x*)||·

o(tf (x*)) ||(tf (x*)||

 0 пpи t 0,

выражение в квадратных скобках в правой части (6) при всех достаточно малых t положительно и поэтому при всех достаточно малых положительных t

f(x_t) < f(x*),

что противоречит тому, что x* = argmin f(x).

Из доказательства следует, что, двигаясь из заданной точки в направлении, противоположном градиенту (говорят в направлении антиградиента), мы локально уменьшаем значение функции. Это замечание потребуется нам в дальнейшем.

Таким образом, минимум функции может достигаться только в тех точках, в которых ее производная обращается в нуль, и поэтому уравнение f (x) = 0,

или, что то же самое, система m (вообще говоря, нелинейных) уравнений с m неизвестными

f(x1, ..., xm) xi

= 0,   i = 1, ..., m,

определяет точки "подозрительные на минимум". Точки, удовлетворяющие уравнению (7), называются стационарными точками функции f.

Стационарная точка x* функции f может быть либо точкой локального минимума, либо точкой локального максимума, либо не быть ни той, ни другой (см. р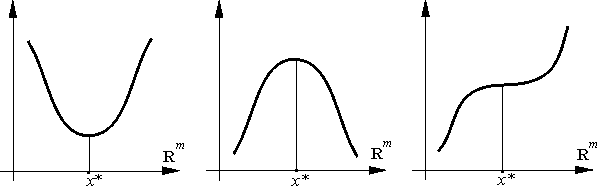ис. 1).

Рис. 1.

Точка (x*, y*) называется седловой точкой функции f: ₁×₂  R (₁  Rⁿ, ₂  R^m), если при всех (x, y)  ₁×₂ выполнены неравенства f(x*, y)  f(x*, y*)  f(x, y*)

(см. рис. 2). Если эти неравенства выполняется лишь для x достаточно близких к x* и y достаточно близких к y*, то, естественно, добавляется эпитет локальная.

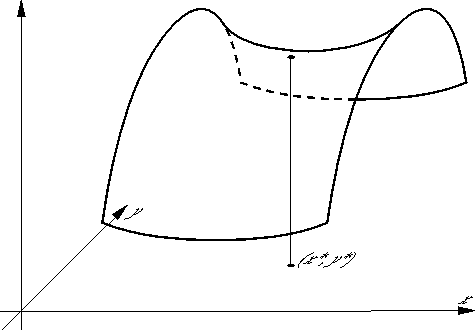Рис. 2.

Легко доказать, что седловая точка непрерывно дифференцируемой функции всегда является стационарной точкой и, очевидно, никогда не является точкой экстремума.

3.5. Теорема о локальном минимуме (необходимые и достаточные условия второго порядка).

Пусть x* — стационарная точка дважды дифференцируемой функции f. Для того, чтобы точка x* была точкой (локального) минимума функции f необходимо, чтобы оператор f ўў(x*) был неотрицательно определен и достаточно, чтобы он был положительно определен.

Д о к а з а т е л ь с т в о. Необходимость. Пусть x* — точка минимума и h — произвольный вектор из R^m. Поскольку (в силу теоремы Ферма) x* — стационарная точка,

0 < f(x* + th)  f(x*) =

1 2

(f (x*)th, th) + o((th)2)

при всех достаточно малых t  R. Отсюда при всех t  0

(f (x*)h, h) +

o((th)2) t2

> 0.

Переходя в полученном неравенстве к пределу при t 0 и учитывая, что как легко видеть, o((th)²)/t²  0 при t  0, получим нужное неравенство (f (x*)h, h)  0.

Достаточность. Пусть f (x*) положительно определен, а стационарная точка x* не является точкой локального минимума. Последнее означает наличие последовательности x ⁿ x* при n   такой, что f(xⁿ) < f(x*). Положим hⁿ = xⁿ  x*. По определению второй производной, учитывая, что x* стационарна,

0 > f(x* + thn)  f(x*) =

1 2

(f (x*)hn, hn) + o((hn)2).

Если теперь обозначить hⁿ/||hⁿ|| через gⁿ, то последнее неравенство (поделив его на ||hⁿ||²) можно переписать в виде

(f (x*)gn, gn) +

o((hn)2) ||hn||2

< 0.

Поскольку ||gⁿ|| = 1, а сфера в R^m компактна, последовательность {gⁿ}, не ограничивая общности, можно считать сходящейся к некоторому лежащему на ней (и следовательно, отличному от нуля) вектору g⁰. Предельный при n   переход в неравенстве (8) приводит к противоречащему положительной определенности оператора f (x*) неравенству (f (x*)g⁰, g⁰)  0.

Теорема доказана.

З а д а ч а  2.6. Исследуйте на экстремум функцию f: R²  R, задаваемую формулой f(x₁, x₂) = x₁²/a+ x₂²/b,при различных a и b.