Тпв графа Мили

В ТПВ Мили в каждой клетке записаны переходы и выходы. Например, если автомат находится в состоянии С0 и на вход приходит буква a1, то он перейдёт в состояние С1 и на выходе появится буква b3.

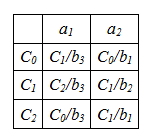
Тпв графа Мура

Для графа Мура строят отмеченную таблицу переходов. Выделяется дополнительный столбец для выходных букв. В клетке под входной буквой пишется в какое состояние автомат переходит, в крайней правой клетке — какую выходную букву возвращает.

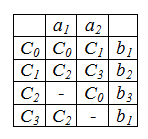
Б И Л Е Т № 22

1. Алгоритм решения краевой задачи для линейного уравнения с постоянными коэффициентами y'' + аy' + by = f(x).

2. Синтез комбинационных автоматов в заданных базисах. Синтез в базисе "И", "ИЛИ", "НЕ". Импликативный базис. Синтез в базисах "И-НЕ" и "ИЛИ-НЕ". Синтез в базисе Жегалкина. Метод каскадов. Булева производная.

Как решить линейное неоднородное уравнение с постоянными коэффициентами вида  ?

Алгоритм решения неоднородного ду следующий:

1) Сначала нужно найти общее решение соответствующего однородного уравнения. Да-да, взять уравнение  , откинуть правую часть:   – и найти общее решение. Данная задача подробно разобрана на уроке Однородные уравнения второго и высших порядков. Общее решение однородного уравнения я привык обозначать буквой  .

2) Наиболее трудный этап. Необходимо найти какое-либо частное решение   неоднородного уравнения. Сделать это можно так называемым способом подбора частного решения с применением метода неопределенных коэффициентов.

Внимание! Для освоения метода подбора будет жизненно необходим методический материалКак подобрать частное решение неоднородного уравнения? Данную справку лучше по возможности распечатать, очень удобно, если она будет перед глазами. Но не спешите вникать в эти таблицы, если являетесь чайником! Всему свое время.

3) На третьем этапе надо составить общее решение    неоднородного уравнения. Это совсем легко:  . Совершенно верно – следует просто приплюсовать завоёванные трофеи.

Если изначально в условии сформулирована задача Коши (найти частное решение, удовлетворяющее заданным начальным условиям), то добавляется четвёртый этап:

4) Нахождение частного решения, удовлетворяющего заданным начальным условиям. Порядок нахождения частного решение для уравнения второго порядка уже немного рассмотрен на уроке Однородные уравнения второго и высших порядков. В случае с неоднородным диффуром принципы нахождения частного решения сохраняются.

Примечание: В ваших лекциях, практических занятиях общее решение однородного уравнения   и подобранное частное решение неоднородного уравнения  , скорее всего, обозначаются не так. Я «намертво» привык к обозначениям  ,    и буду использовать именно их.

Не так всё страшно, переходим к практическим задачам.

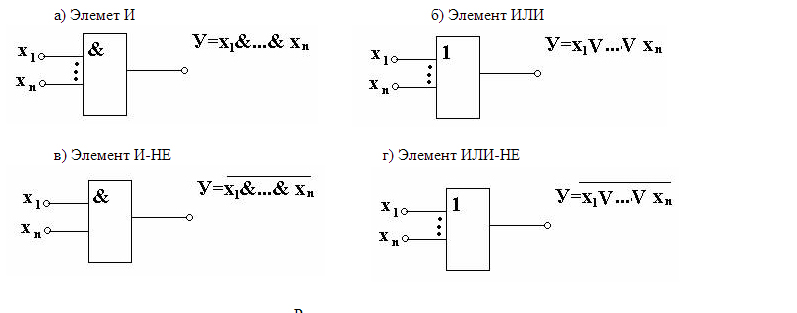
Синтез на основе ДНФ (до 30 минут)  Синтез комбинационного автомата заключается в представлении каждой функции F_i (x₁, .., x_n ) в виде суперпозиции булевых функций реализуемых стандартными (типовыми) логическими элементами и узлами. Наиболее распространенными являются элементы И, ИЛИ, И-НЕ

ИЛИ-НЕ (рисунок 10.1)

 

а) Элемет И                                                                          б) Элемент ИЛИ

 

 

 

 

 

П₆ = {r, b, d}  B₆ = {, &, 1} – базис Жегалкина;

П₃ = {a, n}  B₃ = {, 0} – импликативный базис;

Булевой производной функции f(x) = f(x₁, x₂,..., x_n) по x_i называется функция df(x) / dx_i = f(x₁, x₂,..., x_i,..., x_n) Å f(x₁, x₂,..., ,..., x_n), где                 Å – сумма по модулю 2.

Булева производная может быть также вычислена и по следующей формуле:

df(x) / dx_i = f(x₁, x₂,..., 0,..., x_n) Å f(x₁, x₂,..., 1,..., x_n).

Булева производная определяет значения логических переменных x₁,..., x_n (кроме x_i), при которых изменение состояния x_i приводит к изменению значения функции f(x).

 

 

 

 

 

Б И Л Е Т № 23

1. Свойства решений однородного линейного дифференциального уравнения n-го порядка y(n) + f1(x) y(n-1) + …+ fn(x) y = 0. Понятие фундаментальной системы решений однородного линейного уравнения n-го порядка. Теорема об общем решении этого уравнения.

2. Введение в теорию графов. Мультиграф, подграф, надграф, частичный граф. Степень вершины, смежность, инцидентность. Однородный граф, полный граф, дополнение графа. Объединение и пересечение графов.

Рассмотрим линейное дифференциальное уравнение n –го порядка

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = f(x).

с непрерывными коэффициентами a_n-1(x), a_n-2(x), ..., a₁(x), a₀(x) и непрерывной правой частью f(x).

Принцип суперпозиции основан на следующих свойствах решений линейных дифференциальных уравнений.

1. Если y₁(x) и y₂(x)— два решения линейного однородного дифференциального уравнения

y⁽ⁿ⁾ + a_n-1(x)y^{(n - 1)} + ... + a₁(x)y' + a₀(x)y = 0

то любая их линейная комбинация y(x) = C₁y₁(x) + C₂y₂(x) является решением этого однородного уравнения.

2. Если y₁(x) и y₂(x) — два решения линейного неоднородного уравнения L(y) = f(x) , то их разность y(x) = y₁(x) − y₂ (x) является решением однородного уравнения L(y) = 0 .

 

3. Любое решение неоднородного линейного уравнения L(y) = f(x) есть сумма любого фиксированного (частного) решения неоднородного уравнения и некоторого решения однородного уравнения.

 

4. Если y₁(x) и y₂(x) — решения линейных неоднородных уравнений L(y) = f₁(x) и L(y) = f₂(x) соответственно, то их сумма y(x) =y₁(x) + y₂(x) является решением неоднородного уравнения L(y) = f₁(x) + f₂(x).