3.4. Полосовой усилитель

Одиночные контуры имеют недостаточные высокую избирательность. Это объясняется пологостью скатов резонансной кривой контура. Для повышения избирательности применяются более сложные колебательные системы - чаще двухконтурные.

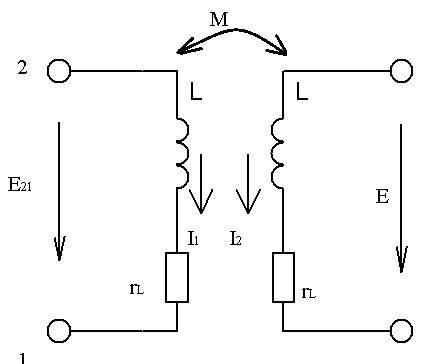
Предполагается, что двухконтурная нагрузка подсоединена к зажимам 1-2 активного элемента, например, лампы:

Вход усилителя – зажимы 3 и 4, выход - зажимы 5 и 6.

Для двухполюсника нагрузки получим эквивалентную схему:

Выделенный пунктиром 4-полюсник:

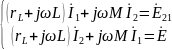
заменим эквивалентной схемой:

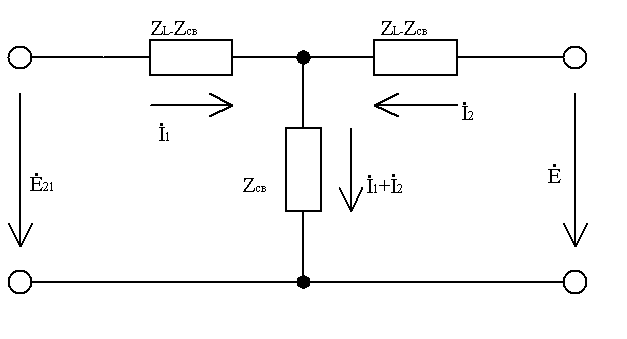
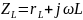
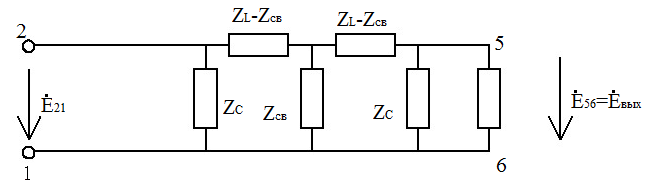
На эквивалентной схеме двухполюсник нагрузки усилителя:

Где

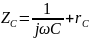
Чтобы найти эквивалентную схему всего усилителя, достаточно к зажимам 1 и 2 слева подключить эквивалентную схему активного элемента.

В случае лампы, эквивалентная схема всего усилителя выглядит так:

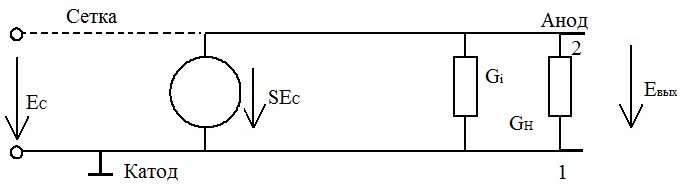
- проводимость нагрузки между зажимами 1 и 2.

Коэффициент передачи по напряжению активного элемента к зажимам 1 и 2 от входа сетка-катод:

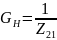
Обозначим коэффициент передачи по напряжению от зажимов 2-1 к зажимам 5-6:

Тогда передаточная функция по напряжению всего усилителя:

Найдем ее выражение при следующих, упрощающих выкладки, предположениях:

Найдём :

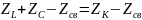
- сопротивление одного контура

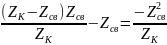
Схема нагрузки упрощается эквивалентно:

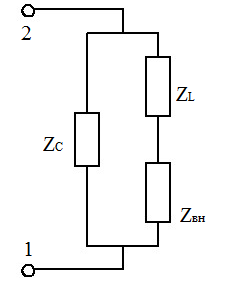
Вывод: Влияние второго контура на связанный с ним, по магнитному потоку, первый контур - отражается, дополнительным включением на эквивалентной схеме, первого контура вносимого сопротивления .

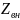Сопротивление связи можно пренебречь по сравнению с , а сопротивление контура вблизи резонанса может быть порядка

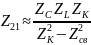
Заметим, что:

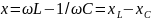
Сопротивление одного комбинированного колебательного контура при резонансе:

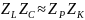
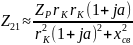
Делим числитель и знаменатель на , обозначим:

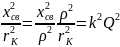
k-коэффициент связи между контурами.

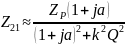
При частоте - резонансная частота контура, имеем:

Найдём передаточную функцию по напряжению от зажимов 2-1 к выходу 5-6

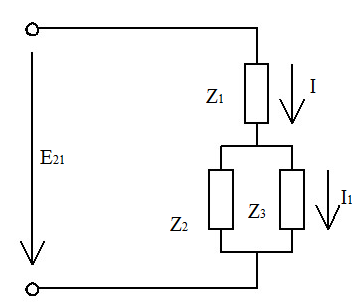
Подставим I во второе уравнение системы:

В этой формуле можно пренебречь

Передаточная функция по напряжению всего усилителя:

Таким образом:

φ

kφ<1

kφ=1 kφ>1

ФЧХ

Где

Анализ АЧХ и ФЧХ:

При резонансе 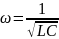следовательно:

Так как a=0

kQ - фактор связи контуров.

При критическом уровне связи kQ=1 достигает максимального значения: 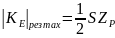, т.е. вдвое меньше, чем у резонансного усилителя.

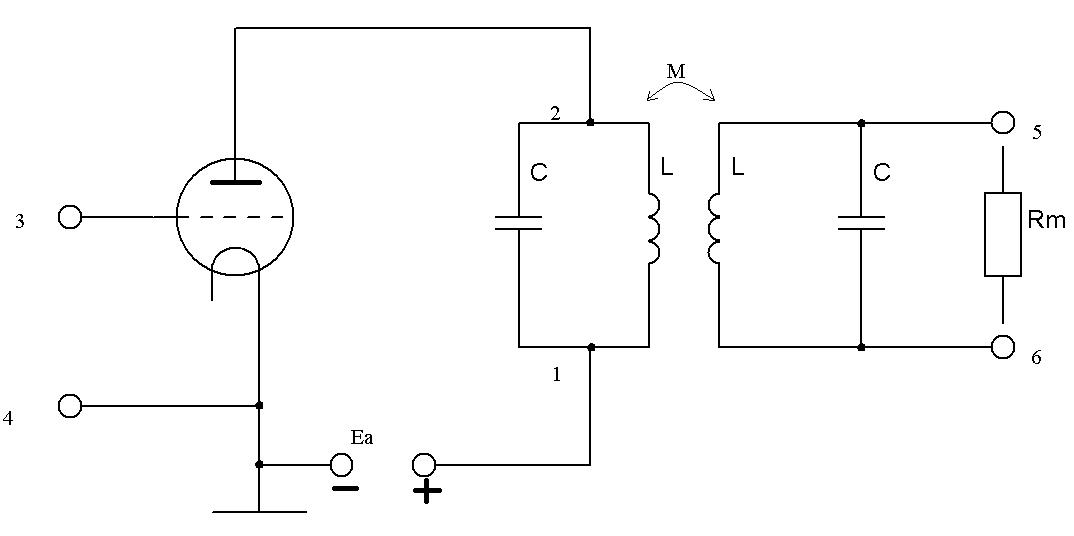
Нормированная резонансная характеристика двухконтурного усилителя:

Где - расстройка контура относительное резонансной частоты.

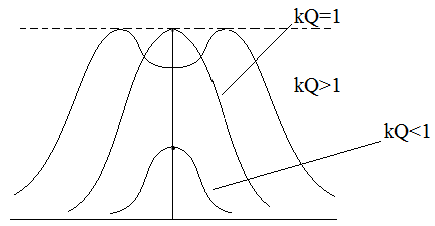
1 n

Чем больше kQ>1, тем глубже провал при a=0 и тем шире расставлены max АЧХ относительно a=0.

При использовании связанных систем в качестве полосовых фильтров обычно исходят из критической связи, когда резонансная характеристика наиболее равномерна в полосе прозрачности и наиболее резко ослабляется при переходе к полосе подавления.

На границах полосы прозрачности n(a) ослабляется в по сравнению с 1(при kQ=1 и a=0)

Чтобы получить ту же величину полосы прозрачности для двухконтурной системы(kQ=1), что и для одноконтурной, надо взять в первом случае контуры с добротностями Q в больше, чем во втором случае.

Но избирательность двухконтурной системы окажется лучше, чем у одноконтурной.