9. Побудуємо амплітудно-фазову характеристику для скорегованої розімкненої сак
Амплітудно-фазовою частотною характеристикою (амплітудно-фазовою характеристикою, АФХ) називається годограф частотної передаточної функції. Годограф комплексної функції будується на комплексній площині. Будь-якому значенню аргументу на комплексній площині відповідає точка. Множина точок, відповідаюча плавній зміні аргументу від - до , утворює криву, яка і називається годографом. Для побудови годографа необхідно виділити дійсну Re(ω) та уявну Im(ω) частини передаточної функції та побудувати їхню графічну залежність
Будуємо за допомогою програми MatLab амплітудно-фазову характеристику (рис.8):
.
Код програми матиме такий вигляд:
w=0:0.001:5;
p=j*w;
W=(17895*p+78.8)./(34.5*p.^4+123.88*p.^3+29.9*p.^2+1);
Re=real(W);
Im=imag(W);
plot(Re,Im);
title('AFH');
ylabel('Im');
xlabel('Re');
grid on;
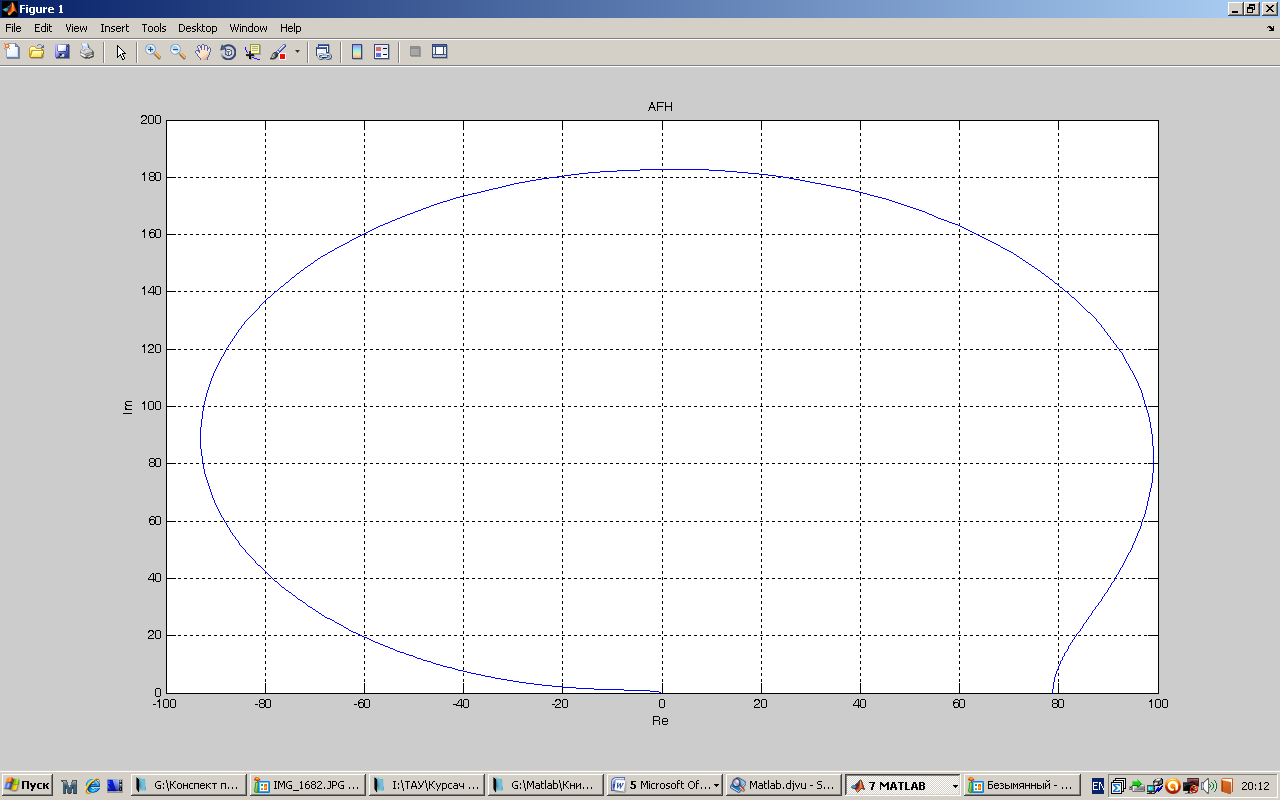
Рис. 8 АФХ розімкненої системи з коригувальною ланкою
10. Побудова перехідної та імпульсної характеристики сак
Перехідною характеристикою САК є реакція системи на одиничне ступінчасте збурення. Імпульсна характеристика відображає реакцію системи на імпульсне збурення.
Д
ля
побудови перехідної та імпульсної
характеристик САК побудуємо модель
замкненої системи регулювання у пакеті
Simulink програми Matlab (рис. 9). Коєфіцієнт
підсилення коригувальної ланки
Рис. 9 Модель системи регулювання у пакеті Simulink
П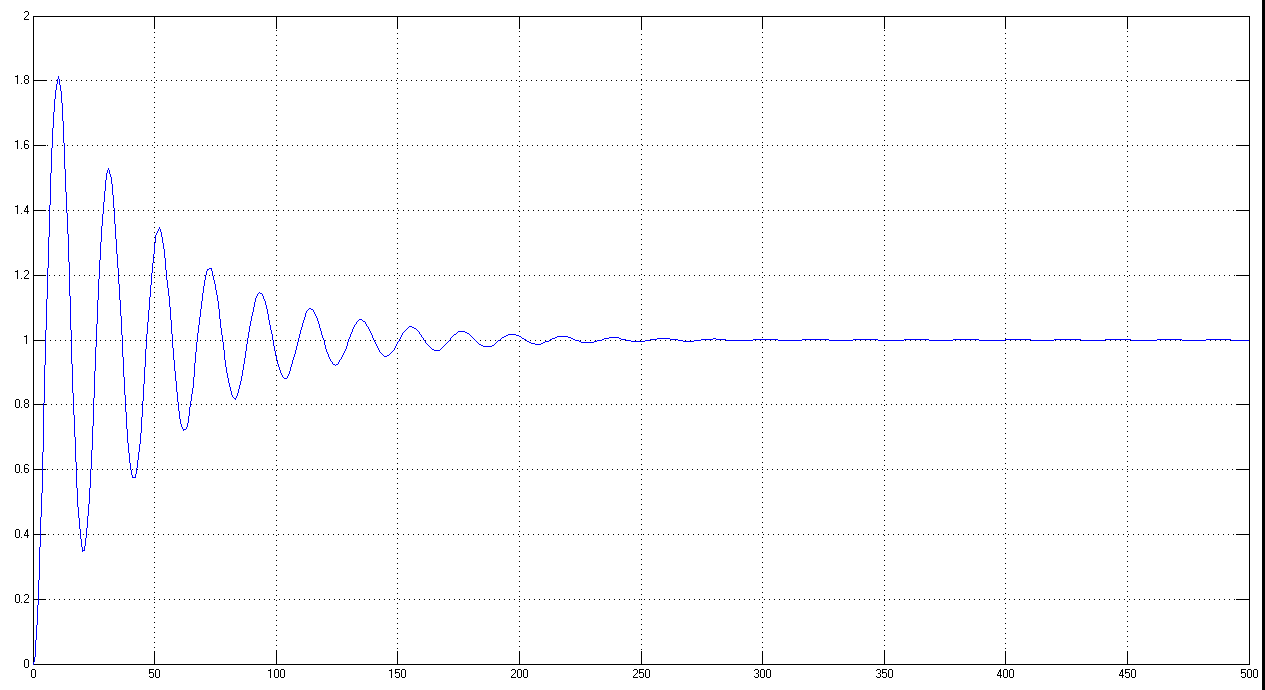
одамо
на вхід системи (збоку завдання)
ступінчастий сигнал,
рівний одиниці. На осцилографі буде
відображено перехідний процес у системі.
Рис. 10 Перехідна характеристика замкненої системи
Як
видно, в системі відсутня статична
похибка, тобто система гарно «відпрацьовує
завдання». Час регулювання складає
сек.
Разом з тим спостерігаються значне пере
регулювання на початку та сильна
коливальність перехідного процесу.
Для визначення імпульсної характеристики системи подамо на вхід моделі нескінченно короткий імпульс. На виході системи за допомогою осцилографа будемо спостерігати реакцію системи на це збурення (рис. 11):
Р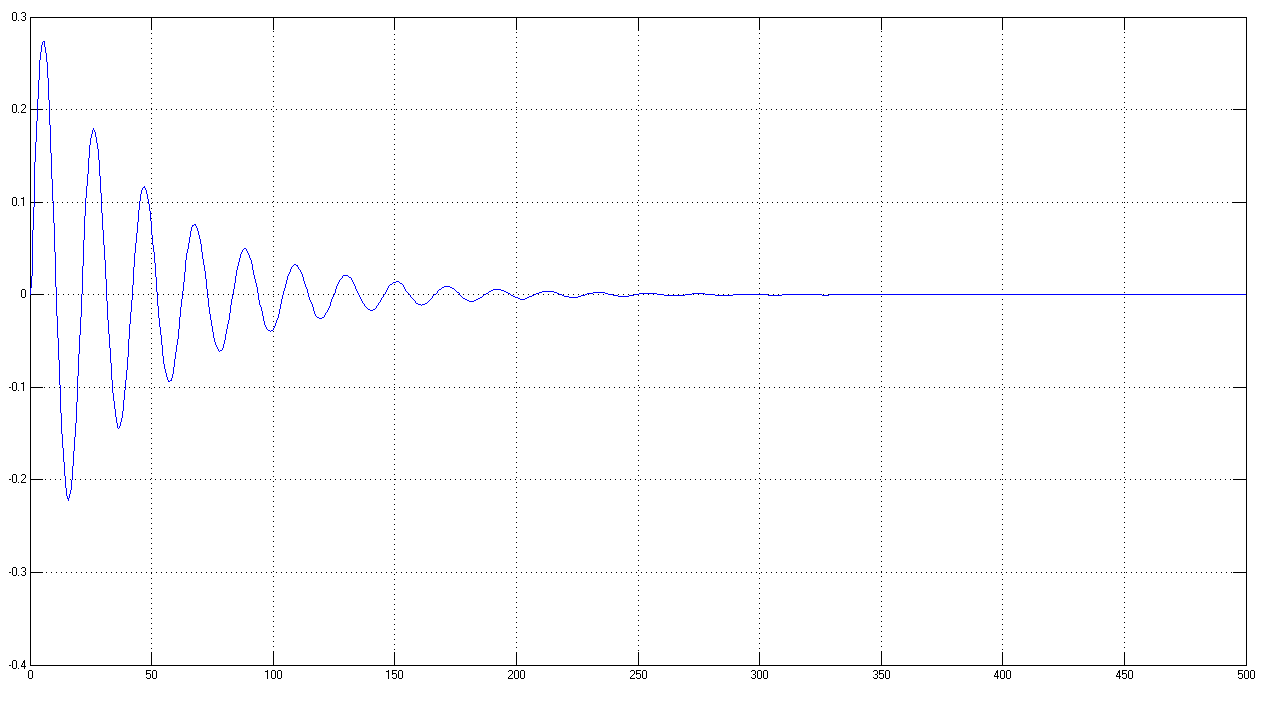
ис.
11 Імпульсна (вагова) характеристика
замкненої системи
За
графіком видно, що система є досить
чутливою до зовнішніх збурень. Хоча
динамічний викид на початку незначний
(
),
проте час затухання перехідних процесів
системи досить значний (
сек).
Література
1. Воронов Теория автоматического управления, части 1 и 2. М.: Высшая школа, 1986.
2.Зайцев Г.Ф.«Теория автоматического управления и регулирования».- Киев:
Вища школа, 1988г.
3.Бесекерский В.А., Попов Е.П. «Теория автоматического регулирования».
М.: Наука, 1974.
4. Крутов В.И. Основы теорииавтоматического управления. М., 1984.