Зміст

Вступ 3

Вихідні дані 4

1. Структурна схема САК кутової швидкості обертання мішалки без врахування коригувальної ланки 5

2. Знаходження виразу для W(р) розімкненої САK і складання диференційного рівняння САР без корекції 6

3. Визначення стійкості САК за допомогою критерію Михайлова 7

4. Побудова структурної схеми САК з введенням заданого коригувального елемента 9

5. Складання диференційного рівняння САК з урахуванням корекції 10

6. Визначення критичного значення коефіцієнта зворотного звя’зку з умов стійкості за Гурвіцем 12

7. Побудова асимптотичних ЛАЧХ та ЛФЧХ розімкненої САК 13

8. Побудова годографа Михайлова для скорегованої САК 15

9. Побудуємо амплітудно-фазову характеристику для скорегованої розімкненої САК. Визначення запасів стійкості за модулем та фазою 17

10. Побудова перехідної характеристики скорегованої САК 18

Література 20

Вступ

Для регулювання вихідної координати і повернення її на заданий рівень створюють системи автоматичного керування (САК). Система автоматичного керування підтримує чи покращує функціонування керованого об’єкта без втручання людини, що значно спрощує працю і дозволяє покращити показники якості роботи процесу, технологічної лінії.

Розвиток теорії автоматичного керування в останні роки є плідним і багатогранним. В автоматизованих системах керування технологічними процесами роль динаміки безперечна.

Передбачається впровадження автоматизованих систем у різноманітні сфери господарської діяльності, і в першу чергу в приготування, керування обладнанням і технологічними процесами. У вирішенні цих задач дослідження і розробки в області теорії автоматичного керування відіграють важливу роль.

Вихідні дані

Передатні функції:

• об’єкта керування - ;

• чутливого елемента - ;

• виконавчого елемента - ;

• підсилювача - ;

• коригувальної ланки - .

Коефіцієнти підсилення:

Сталі часу:

1. Структурна схема сак кутової швидкості обертання мішалки без врахування коригувальної ланки

1.1. Функціональна схема системи автоматичного регулювання кутової швидкості мішалки ферментера без врахування корекції

Складемо функціональну схему САК кутової швидкості мішалки ферментера без врахування корекції (див. рис.1), яка складається з об’єкта регулювання, чутливого елемента підсилювача та виконавчого механізму.

Рис 1. Структурна схема САК без врахування коригувального елементу

1.2. Структурна схема САК кутової швидкості мішалки ферментера без врахування корекції

Підставляючи в функціональну схему САК передатні функції кожного елемента отримаємо структурну схему САК (див. рис.2).

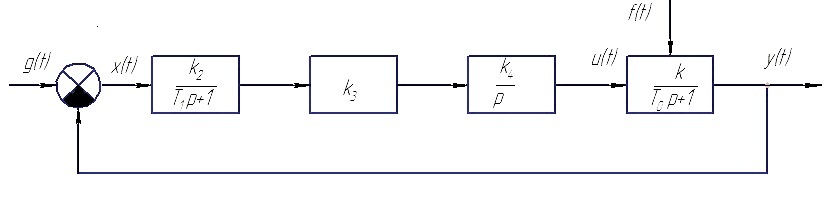
Рис. 2 Структурна схема САК без врахування коригувального елементу

2. Знаходження виразу для Wр розімкненої саk і складання диференційного рівняння сар без корекції

2.1. Вираз для загальної передатної функції W_р розімкненої САК:

Підставимо в формулу вихідні дані, отримаємо характеристичне рівняння:

(1)

2.2. Вираз для передатної функції замкненої системи

Головна передатна функція замкненої системи керування, в загальному випадку, має вигляд:

, або .

Прирівнявши праві частини виразів для Ф(p) отримаємо:

(2)

Підставивши рівняння (1) в рівняння (2) і помноживши ліву і праву частини отриманого рівняння на знаменник рівняння (1) отримаємо диференційне рівняння системи автоматичного керування без врахування корекції:

3. Визначення стійкості сак за допомогою критерію Михайлова

Розглянемо окремо характеристичний поліном системи:

де p= jω.

Згідно критерія Михайлова, для того щоб система була стійкою, необхідно, щоб повний приріст аргумента ψ(ω) при зміні частоти ω від 0 до ∞ дорівнював n , де n це порядок полінома D(p).

3.2. Побудова годографа Михайлова

Для того, щоб побудувати годограф Михайлова, виділимо дійсну та уявну частини характеристичного поліному D(p) та побудуємо їх залежність.

Для цього скористаємось програмним продуктом Matlab 7:

w=0:0.001:0.5; %діапазон(від 0 до 5) та крок (0.001) зміни частоти ω

p=j*w;

D=1+(38.88./(115*p.^3+29.6*p.^2+p));%задаємо поліном D(p)

Re=real(D); %виділяємо дійсну частину

Im=imag(D); %виділяємо уявну частину

plot(Re,Im);

title('Godograf Mihailova');

ylabel('Im');

xlabel('Re');

grid on;

Результат виконання програми наведено на рис.3. З графіку видно, що годограф починається у точці ω=0, але перші три квадранти проходить непослідовно (відразу переходить у другий квадрант), тобто система автоматичного керування є нестійкою.

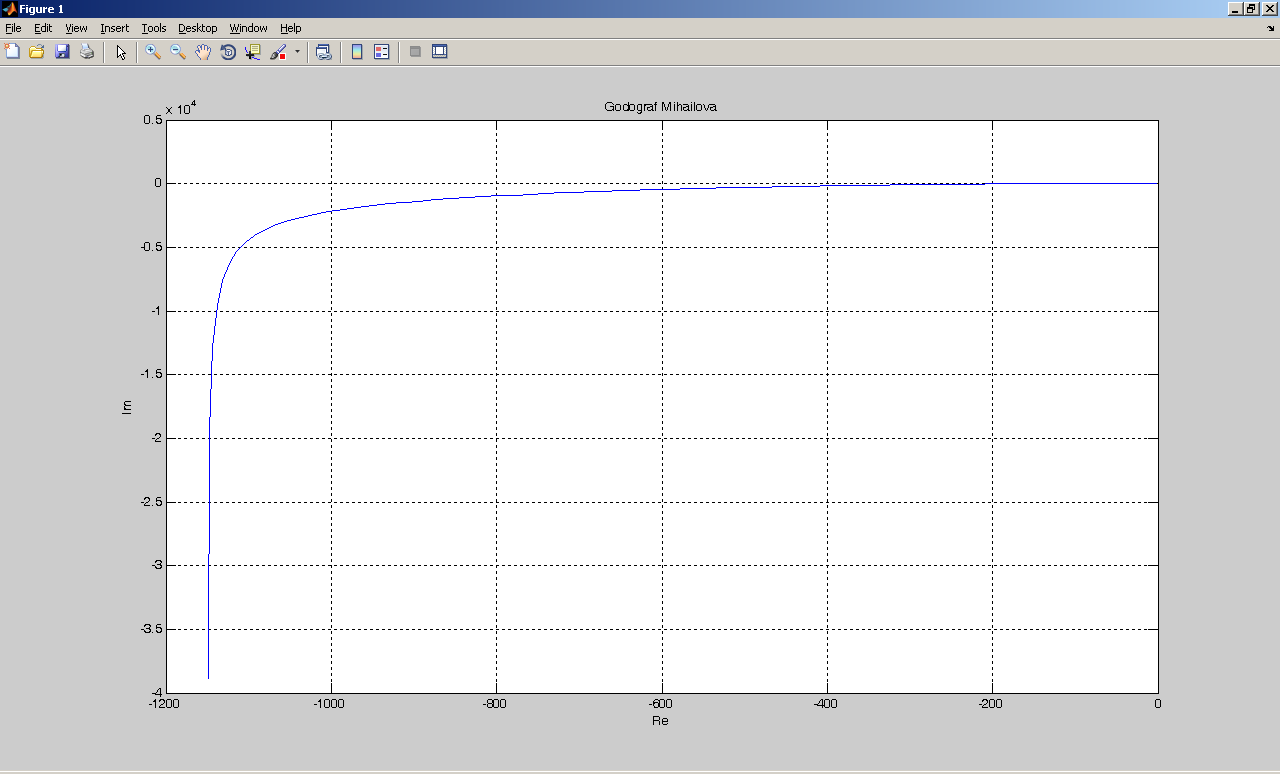Рис. 3 Годограф Михайлова системи без коригуючої ланки

4. Структурної схема сак з введенням заданого коригувального елемента

4.1. Побудова структурної схеми САК з урахуванням коригувального елемента (див. рис.4)

Рис 4. Структурна схема САК із врахуванням коригувального елементу

де - передатна функція чутливого елемента;

- передатна функція підсилювача;

- передатна функція виконавчого елемента;

- передатна функція об’єкта керування.

- передатна функція коригувальної ланки.