45. Графічний метод побудови перехідних процесів по дійсних частотних характеристиках. (Метод трапецій).

Цей метод дозволяє визначити вираз: , при апроксимації сумою трапецевидних частотних характеристик.

1. Визначають приведену дійсну частотну характеристику: , .

2. Графік апроксимують декількома трапецевидними частотними характеристиками. Кожна трапецевидна частотна характеристика характеризується параметрами , , : .

3. Визначають коеф нахилу кожної трапецевидної частотної характеристики χ .

4. Дано таблиці функції. З допомогою таблиць - функцій по визначених коеф нахилу виписують значення і .

5. Розраховують елементарні перехідні характеристики, які відповідають еальним значенням і . Для цього ординати одержані в попередньому пункті одиничних - функцій множать на і знаходять , а значення аргумента ділять на , . - це функціїї яким відповідають такі частотні характеристики: .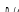

46. Інтегральні оцінки якості перехідних процесів.

Інтегральні оцінки якості дають загальну оцінку швидкодії і відхилення керованої величини від усталеного стану. . – відхиленння керованої величини від нового усталеного стану яке приймає керована величина після закінчення перехідного процесу. , , – відхилення омилки, або розузгодження. Якщо візьмемо похідну , , , . . . = . . Звідки випливає, що інтегральний критерій ( ) залежить від параметрів ланок системи початкових умов і похідних від початкових умов. , . Недоліком цього критерію є те що використовується тільки для монотонних або аперіодичних процесів. Якщо є коливний процес, площі сумуються алгебраїчно і мінімум інтегралу І₁. Може відповідати коливанням з малим затуханням, або взагалі без затухання.

47. Послідовні корегуючі ланки в контурі сак.

А) Пропорційно- диференціююча ланка.

1. ідеальна пропорційно диференціююча ланка (ПД). , – пропорційний коефіцієнт. . ; . Якщо система замикається, то . , як правило: то . Видно, що введення ПД ланки дозволяє змінити величину коеф при в многочлені .

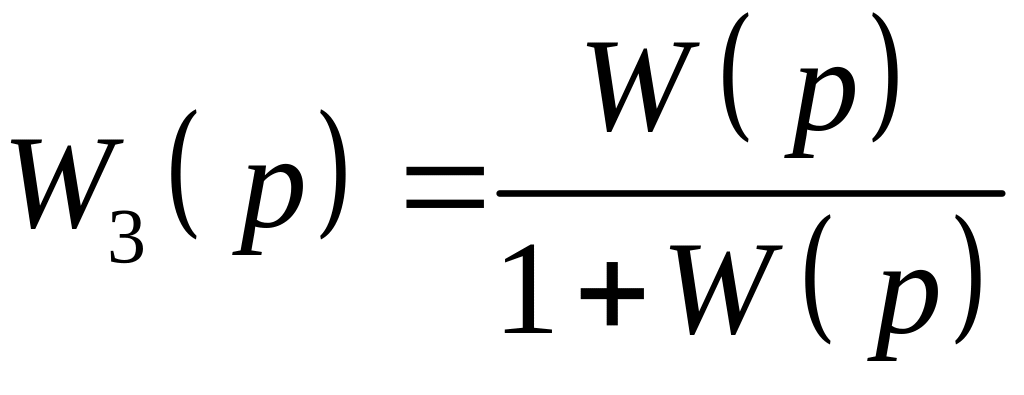Можлива також зміна коефіцієнта при р вищих порядків. Використання ПД ланки для забезпечення стійкості системи з астатизмом вищим першого порядку. , при р=0, очевидно, що в і звідси маємо: , , видно, що система структурно нестійка з порядком астатизму є структурно нестійкою, так як в виразі відсутні члени з в степені від .

Введемо в систему ПД ланки, які дають додатні додаткові дії по похідних від першого до порядку.

. , = . Тким чином система стала структурно стійкою. Аналогічно можна з допомогою додаткових дій по похідних зробити структурно нестійку систему стійкою в якої попередньо мав від’ємні коефіцієнти.

Вплив ПД на якість перехідного процесу: 1. Характеристика відповідає від’ємній дії по похідні. 2. Характеристика відповідає додатній дії по похідній. 3. Характеристика одержана при збільшені вдвоє додатнього коеф К_д. Звідки видно, що додаткова дія на похідній знижує швидкодію, а додатня наоборот підвищує швидкодію.