18. Коливна ланка.

Диф рівняння.

, а для коливної ланки: , Т₀=Т.

Вводимо коеф димферування: , можна представити: . Де - кутова частота вільних коливань (при відсутності загасання). Коеф демферування для коливних ланок: ,

.

Передавальна функція: , аналогічно і W(S). Приклади:

18.1. Коливне RLC – коло.

18.2. Двигун постійного струму незалежного збудження.

18.3. Пружні мех передачі.

18.4. Гіроскопічні елементи (які можуть визначити в будь-який момент де він).

19. Консервативна ланка.

Частковий випадок коливної ланки, коли коеф демферування рівний нулю.

. , .

Перехідна функція, перехідна характеристика. .

.

АФЧ

q – частота вільних коливань. Мал19.1.

Амплітудна частотна функція:

Фазочастотна характеристика. , .

то , то .

.

Логарифмічна амплітудна характеристика. .

20. Інтегруюча ланка.

, py=kx. , .

Приклади:

20.1. Операційний підсилявач в режимі інтегрування. Взворотньому зв’язку стоїть конденсатор.

20.2. Гідравлічний демпфер. Гідравлічний сервер двигун. Інтегруючий привід.

Перехідна характеристика: h(t)=kx.

Імпульсна перехідна характеристика .

Комплексна передавальна функція. .

. .Логарифмічна амплітудна характеристика : .

Із збільшенням частоти, сигнал послаблюється.

21. Інтегруюча ланка з сповільненням.

, в оперативній формі: , або .

Передаточна функція: , в формі перетворення Лапласа: . Часові функції:

Перехідна функція: . Та сама характеристика, тільки зміщена на деяку величину.

Імпульсна перехідна характеристика:

Амплітудно фазо частотна функція. . , Логарифмічна. Коли 40 – то нехтуєм 1 , коли 20 то під коренем.

22. Ізодромна ланка. . , ,

Передаточна функція в операторній формі:

, - безінерційна , - постійна часу ізодромної ланки.

Ізодромну ланку можна представити у вигляді паралельно з’єднаних двох ланок:

Ідеально інтегруючої, та безінерційної.

Безінерційний підсилювач з RC ланкою в зворотньому зв’язку.

2. Комбінація демпфера з спружиною:

Ізодромна ланкка на базі інтегруючого приводу.

Перехідна функція:

Імпульсна перехідна функція і характеристика: , t= 0 то .

Подали імпульс і він пішов рівно, паралел абцисі.

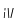Амплітудно фазочастотна функція: = . АФХ ізодромної ланки:

Амплітудна частотна функція: . .

Логарифмічна амплітудна характеристика. .до 1/Т то 20lg .

23. Ідеальна диференціююча ланка.

, у=kpx, , .

Приклади: Тахогенератор постійного стуму, х= , у=е.

Операційний підсилювач в режимі диференціювання:

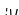Часова перехідна h(t)=ks(t): . Імпульсна хаактеристика: Графік подібн, тільки замість h(t) . АФЧ функція: .

АЧФ іАЧХ

то .АЧХ: :

Логарифмічна частотна функція: .

24. Диференціююча ланка з сповільненням. , .

Передавальна функція в операторній формі: . .

Приклади: RC-ланка, RL- ланка, трансформатор напруги(х=U₁, y=U₂). Перехідна характеристика: .

Імпульсна перехідна функція: , .

АФЧ функція: , .

АЧФ : , . : . 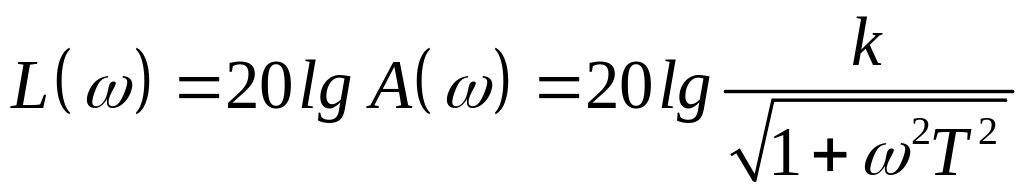, - нехтуємо до : . , , після нехтуємо 1 .

Ланка з постійним запізненням: , , , , . Ланки закінчились.

25. Передаточна функція послідовно з’єднаних ланок.

. , , , . Очевидно, що , , , де W(p) – передаточна функція всієї системи послідовно з’єднаних ланок, тобто = добутку передаточних функцій всіх ланок. .

26. Передаточна функція паралельно з’єднаних ланок.

, , , то =W(p). Тобто записано так: . Визначення: Передаточна функція групи паралельно з’єднаних ланок=сумі передаточних функцій цих ланок.

27. Ланки охоплені зворотнім зв’язком.

Х_33­ –сигнал зворотнього зв’язку. , , . , .

Передаточна функція замкнутої системи: .

Передаточна функція розімкнутої системи: .

„--” коли додатній зворотній зв’язок.

„+” коли від’ємний зворотній зв’язок.

. Знайти: , , .

, передаточна функція: , . .

. - один в чисельлнику, тому що немає передаточної функції між х і .

28. Правила переносу вхідних і вихідних сигналів в структурних схемах.

28.1. Перенесення елементу сумування: після: . . Перенесення точки розгалуження: після : , .

30. Стаціонарний режим статичних систем.

Статичний стаціонарний режим це режим при якому система знаходиться в стані спокою в результаті того, що всі зовнішні дії і параметри системи не змінюються в часі.

Статичний режим статичних систем. Статичні системи це системи які не мають інтегруюючих ланок. . . . Де у_СТ – статичний приріст, або статичне відхилення вихідної величини, що викликане приростом f_{Статичне}.

, , тоді . Де К= - коефіцієнт передачі розімкнутої системи попередньо приведеної до одноконтурного вигляду.

коеф. Передачі ділянки системи від місця прикладення дії f до місця знаходження вихідної величини у. величина статичного відхилення що припадає на одиницю дії f. Це величина є мірою статичної точності системи. , .