Затухающие колебания

В

реальных условиях любое движение всегда сопровождается процессами диссипации, т. е. необратимого поглощения и рассеяния энергии. Роль диссипативного элемента в электромагнитных цепях выполняет резистор. Каждую секунду резистор, согласно закону Джоуля - Ленца, превращает в тепло (за счет рассеяния носителей тока на неоднородностях структуры и состава материала) мощность Р = I²R.

Покажем, что собственные колебания заряда и тока в реальном колебатель­ном контуре, содержащем помимо конденсатора и катушки еще и резистор, являются затухающими, т. е. их амплитуда монотонно убывает со временем. Применим закон сохранения и превращения энергии и получим дифференциальное уравнение затухающих колебаний (ДУЗК) в реальном контуре (контуре с сопротивлением и потерями энергии).

P = I²R = - dW/dt = - d/dt(q²/2C + LI²/2)  (dq/dt)R = - (2q/LC)dq/dt + 2(dq/dt)d²q/dt²  d²q/dt² + q/LC + (R/L)dq/dt = 0 

 d²q/dt² + 2dq/dt + _о²q = 0 – ДУЗК.

где: _о = 1/(LC) - собственная частота свободных (незатухающих) колебаний в контуре;

 = R/2L - коэффициент затухания колебаний:

Решить полученное уравнение можно путем замены переменной: q = Qе^-t.

Подставив в дифференциальное уравнение выражения для заряда q = Qе^-t и его производных dq/dt = е^-tdQ/dt – Qе^t и второй d²q/dt² = е^-td²Q/dt² – 2dQ/dtе^-t + ²Qе^-t, получим после сокращения дифференциальное уравнение для новой переменной Q;

е^-td²Q/dt² – 2dQ/dtе^-t + ²Qе^-t + 2е^-tdQ/dt – 2²Qе^-е + _о²q = 0  d²Q/dt² + (_о² – ²)Q = 0,

которое представляет собой дифференциальное уравнение гармонических колебаний величины Q: Q = Q_мcos (t + ), где  = (_о² – ²).

Возвращаясь к исходной переменной - заряду q, получим:

q = Qе^-t = Q_ме^-tcos (t + ) = q_м(t)cos (t + )

Колебания заряда происходят по гармоническому закону, но с экспоненциально убывающей во времени амплитудой q_м(t) = Q_ме^-t. Частота свободных затухающих колебаний  = (_о² – ²) понижается с ростом затухания. Затухание уменьшает среднюю силу разрядного и перезарядного тока в контуре и затягивает тем самым процессы разряда и перезаряда конденсатора, увеличивает период колебаний, уменьшает их частоту.

Д

ля достаточно большого затухания, при котором   _о процесс возвращения системы к состоянию равновесия пере­стает быть колебательным (частота колебаний  = (_о² - ²) становится мнимой). В этом случае имеет место процесс релаксации - апериодического, монотонного возвращения системы к положению равновесия (монотонный разряд конденсатора; вся энергия разрядного тока успевает перейти в теплоту, рассеяться на рези­сторе за время меньшее периода колебаний).

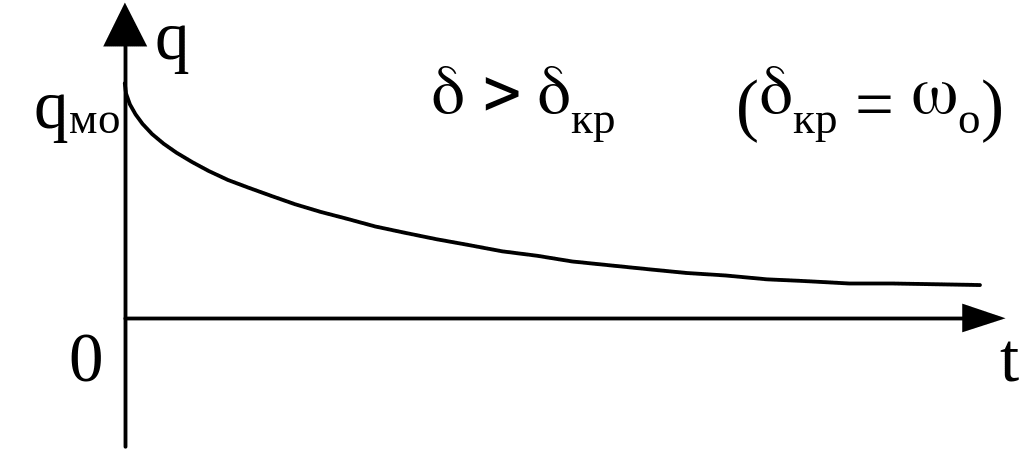
Коэффициент затухания  является мерой быстроты убывания амплитуды колеба­ний. Численно он равен обратному времени релаксации  - времени, за которое амплитуда колебаний уменьшается в е = 2,72 раз: q_м/q_мо = е^- = е^-1 = 1/е.

Коэффициент затухания и время релаксации - недостаточно адекватные характеристики затухания, ибо не соотнесены с «естественным» временным масштабом самих колебаний - их периодом Т. Поэтому вводят еще такую меру затухания колебаний, как декремент D затухания, численно равный отношению двух «соседних» амплитуд, то есть амплитуд, разделенных во времени периодом Т:

D = q_м (t)/q_м(t + T) = q_мое^-t/q_мое^{-(t + T)} = е^-t/(е^-tе^-T) = е^T

Еще более удобной характеристикой затухания колебаний является логарифмический декре­мент затухания  = ln D = Т Его наглядная интерпретация - величина обратная числу колебаний N_е, совершающихся за время релаксации . Действительно:

 = Т = Т/ = 1/(/Т) = 1/N_е, где N_е = /Т.

Рассмотрим фазовые соотношения между колебаниями заряда и силы тока в реальном контуре (с потерями энергии, с затуханием).

q = q_мо е^-t cos (t + ),

I = dq/dt = q_мо(-) е^-t cos(t + ) - q_мое^-t sin(t + ) = q_мое^-t{-cos (t + ) - sin(t + )} = _оq_мое^-t{(-/_о)cos (t + ) - /_оsin(t + )} = _оq_мое^-tcos(t +  + )

(-/_о = cos ; /_о = sin 

tg  = - /

 - угол сдвига фаз между колебаниями заряда и силы тока.

Ток опережает по фазе заряд на угол , зависящий от  и . При  = 0 (нет потерь, затухания)  = /2.

Лекция 11. Вынужденные колебания заряда и тока в контуре. Физическая сущность явления резонанса.

Для получения незатухающих электромагнитных колебаний в контуре к нему необходимо извне подводить энергию, компенсирующую потери на джоулево тепло в электросопротивлении. Для этого к контуру подключают внешний источник переменного тока, который создает в н

ем вынужденные колебания заряда и тока. Рассмотрим особенности вынужденных колебаний в R-L-C контуре при подключении к нему внешнего источника с гармонически изменяющейся ЭДС  = _мcos t.

Дифференциальное уравнение колебаний заряда в R-L-C контуре можно получить на основе как энергетического, так и «силового» подходов. С энергетических позиций мощность источника тока Р_и = I расходуется на изменение электрической и магнитной W_м энергий конденсатора и катушки и на восполнение джоулевых потерь Р_R в электросопротивлении:

Р_и = d/dt(W_э + W_м) + Р_R  Р_и = d/dt (q²/2C + LI²/2) + I²R

Произведя преобразования, аналогичные проведенным ранее при анализе свободных и зату­хающих колебаний, получим в итоге каноническую форму дифференциального уравнения вынуж­денных колебаний заряда:

d²q/dt² + 2dq/dt + _о²q = (_м/L)cos t

Полученное уравнение является неоднородным, и его решение состоит из общего решения соответствующего однородного уравнения (с полагаемой нулю правой частью) и частного решения неоднородного уравнения.

Общее решение однородного уравнения было уже рассмотрено и проанализировано ранее при анализе затухающих колебаний. Оно имеет место на этапах установления стационарного режима вынужденных колебаний. В установившемся же режиме характер колебаний заряда будет определяться (навязываться) правой частью неоднородного уравнения, то есть внешней ЭДС, играющей роль вынуждающей силы. Эти вынужденные колебания заряда будут происходить по закону внешней ЭДС (гармоническому), то есть с ее частотой  и с возможным отставанием по начальной фазе на некоторый угол :

q = q_м cos (t - )

Задача заключается в отыскании амплитуды q_м и начальной фазы  вынужденных колебаний и в выявлении их зависимости от характеристик вынуждающей ЭДС и собственных характеристик колебательного контура.

Подставив в дифференциальное уравнение вынужденных колебаний заряда первую q и вторую q производные от q = q_м cos (t - ), получим:

²q_мcos (t - ) - 2q_мsin (t - ) + _о²q_мcos (t - ) = (_м/L)cos t.

Приведем все тригонометрические функции к единой - косинусу:

²q_мcos (t -  + ) + 2q_мcos(t -  + /2) + _о²q_мcos (t - ) = (_м/L)cos t.

Получили тригонометрическое равенство, в котором сумма трех гармонических функций - колебаний одинаковой частоты, приравнивается к четвертой - вынуждающей «силе». Решение такого уравнения удобно провести с помощью векторной диаграммы. На ней гармоническое колеба­ние изображается в виде вектора, модуль (длина) которого равен амплитуде колебания, и который вращается вокруг оси (Х или У) c угловой скоростью, равной частоте  колебания, будучи в началь­ный момент наклоненным к оси под углом, равным начальной фазе колебания. Так как все колеба­ния имеют одинаковую частоту, изображающие их векторы будут вращаться с одинаковой скоро­стью, и их относительная взаимоориентация с течением времени будет оставаться неизменной.

В

екторная диаграмма позволяет заменить сло­жение гармонических функций (колебаний) одинаковой час­тоты сложением векторов, что значительно проще и нагляднее. Изобразим на векторной диаграмме связь гармонических функций, даваемую уравнением вынуж­денных колеба­ний.

Из векторной диаграммы выразим искомые началь­ную фазу  и амплитуду q_м вынужденных колебаний заряда в контуре:

tg  = 2q_м/[(_о² - ²)q_м];

  = arctg{2/[(_о² - ²)}

(_м/L)² = [(_о² - ²)q_м + (2q_м)²

 q_м = (_м/L)/[(_о² - ²) + 4²²]

П

олученные выражения показывают, что амплитуда и фаза вынужденных колебаний заряда в контуре зависят от коэффициента затухания  и соотношения частот _о и  (свободных колебаний и вынуждающей силы). Графики зависимостей q_м() и (), называемые, соответственно, ампли­тудно- и фазочастотными характеристиками (АЧХ и ФЧХ) заряда для разных значений коэффици­ента затухания , играющего роль параметра в зависимостях q_м() и (), имеют следующий вид:

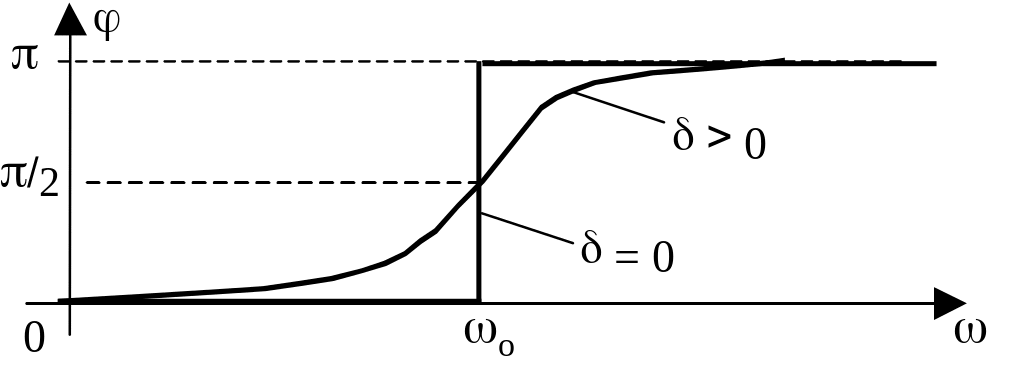
На графике зависимости амплитуды q_м вынужденных колебаний заряда в контуре от частоты  внешнего источника имеет место максимум. Это явление или особенность АЧХ называют резо­нансом. Резонансная частота _р, соответствующая максимуму q_м, формально определяется из усло­вия экстремума функции q_м():

q_м() = 0  _р = (_о² - 2²) (_р  _о)

Затухание колебаний, его мера - коэффициент  - понижает резонансную частоту _р и уменьшает резонансную амплитуду q_мр вынужденных колебаний заряда в контуре (с увеличением  максимумы АЧХ понижаются и смещаются в область меньших частот - резонанс «левеет» и «тупеет»).

Резонансную амплитуду q_мр найдем, подставляя в формулу q_м() значение резонансной частоты _р = (_о² - 2²):

q_мр = (_м/2L)/(_р² - ²).

В отсутствие затухания (при  = 0) значение резонансной амплитуды q_мр = . Это естествен­ный результат, реакция вынужденных колебаний на вынуждающую силу в отсутствие диссипации, поглощения энергии внешнего источника, которые только и могут ограничить амплитуду вынуж­денных колебаний.

При  = 0 имеем статический случай с внешним источником постоянного тока. На конденса­торе имеет место статический заряд

q_{м о} = q_{м ст} = С_м = _м/_о²L (_о² = 1/LC)

При  =  амплитуда вынужденных колебаний заряда равна нулю; вследствие инертности и диссипации колебания не успевают «раскачиваться» с бесконечно высокой частотой, скоростью.

При достаточно большом затухании  > _кр = _о/2 резонансная частота становится мнимой; вместо резонансной зависимости (с максимумом) имеет место монотонный спад амплитуды вынуж­денных колебаний заряда при увеличении частоты внешнего источника. Диссипация, то есть необра­тимый перевод в тепло энергии внешнего источника, преобладает здесь над упругостью и инертно­стью.

Анализ фазочастотной характеристики показывает, что вынужденные колебания всегда отстают по фазе от вынуждающей силы (следствие всегда запаздывает от причины). Это отставание-запаздывание увеличивается с ростом затухания в колебательной системе. При нулевом затухании ( = 0) угол  отставания по фазе вынужденных колебаний заряда от внешней ЭДС скачком изменя­ется на  (от 0 до 180) при  = _о, то есть на частоте собственных колебаний системы (контура).

На частотах, меньших _о, колебания заряда в контуре совпадают по фазе с вынуждающей ЭДС, а на частотах, превышающих _о, заряд колеблется в противофазе с колебаниями внешнего источника.

Колебания силы тока I = dq/dt в контуре также носят резонансный характер, то есть зависи­мость их амплитуды I_м от частоты вынуждающей ЭДС имеет максимум. Но в отличие от резонанса заряда, резонанс тока в контуре всегда происходит на одной частоте, равной частоте _о свободных колебаний в контуре. Формально это связано с тем, что в выражении для амплитуды силы тока I_м = q_м появля­ется еще один множитель - частота . Поэтому характер частотной зависимости I_м() становится отличным от q_м():

I

= dq/dt = - q_мsin (t - ) = I_мcos (t -  + /2),

где I_м = q_м = (_м/L)/[(_о² - ²) + 4²²]   dI_м/dt = 0 при  = _о = 1/(LC)

В чем же причины и физический механизм такого специфического эффекта, как резонанс? Почему вынужденные колебания особенно эффективно возбуждаются на определенной частоте вынуждающей силы? Как и в случае механических колебаний причины резонанса электромагнитных колебаний (заряда и тока) кроются в фазовых соотношениях, то есть резонанс является эффектом амплитудно-фазовым. На резонансной частоте вынужденные колебания силы тока, то есть быст­роты, скорости колебаний заряда, оказываются сфазированными с колебаниями внешнего источ­ника, возбуждающего вынужденные колебания в контуре. Колебания же заряда, которые отстают по фазе от колебаний тока на /2, на резонансной частоте отстают на /2 и от колебаний внешнего источника.

Именно на резонансной частоте создаются наиболее благоприятные, оптимальные условия для перекачки энергии внешнего источника в контур, для потребления ее на раскачку собственных колебаний в контуре. На резонансной частоте вынуждающая сила в течение всего периода колеба­ний действует в направлении (синфазно, синхронно) скорости (перемещения) вынужденных колеба­ний и совершает максимальную работу по их раскачке, наращиванию их амплитуды. Из механики следует, что источник развивает наибольшую мощность N

N = dА/dt = d /dt = = F  cos ,

когда сила сонаправлена со скоростью перемещаемого тела. В случае гармонического характера воздействия (и отклика) эта сонаправленность выражается в сфазированности (синфазности) во времени вынуждающей силы и скорости вынужденных колебаний.

На частотах, как меньших, так и больших резонансной, то есть при   _р, сфазированность внешнего источника и вынужденных колебаний нарушается. При этом лишь часть периода внешний источник совершает положительную работу по раскачке вынужденных колебаний в контуре; в тече­ние же другой части эта работа оказывается отрицательной, тормозящей вынужденные колебания.

При    отставание вынужденных колебаний по фазе от вынуждающей силы достигает 180, и положительная работа внешнего источника сравнивается с его отрицательной работой, результатом чего является стремление амплитуды вынужденных колебаний к нулю (вынужденные колебания не возбуждаются).

Лекция 12. Вещество в магнитном поле. Магнитные моменты атомов. Намагниченность вещества. Магнитная проницаемость. Физическая природа диа- и парамагнетизма. Ферромагнетики.

Вещественные тела состоят из атомов, а в состав атомов входят движу­щиеся заряженные частицы - электроны и протоны. Внутриатомное движение этих частиц может быть подразделено на орбитальное и собственное, назы­ваемое ещё спиновым. Так, например, электрон в атоме вращается вокруг ядра, а также обладает собственным (внутренним) вращением. Каждое из этих вращательных движений может быть уподоблено некоторому круговому витку с током, магнитной характеристи­кой которого служит магнитный момент = IS . Например, для орбитального движения электрона:

 = q_е = q_е/Т, S = r² и Р_m = q_еr²/Т = q_еr/2, где q_е = - 1,610^-19 Кл – заряд электрона,  и Т - частота и период вращения электрона, а r – радиус орбиты электрона в атоме.

Магнитный момент характеризует собственное (спиновое) вращение, как электрона, так и протона, а также и нейтрона, хотя послед­ний является электрически незаряженной частицей.

Таким образом, наличие магнитных характеристик (магнитных моментов) является неотъем­лемой особенностью всех элементарных частиц, входящих в состав атомов. Соответственно, все вещественные тела могут, как создавать собственное магнитное поле, так и взаимодействовать с внешним магнитным полем. Мерой магнитных свойств вещества является магнитная проницаемость , численно равная отношению индукции В магнитного поля в веществе к индукции В_о магнитного поля в вакууме:

 = В/В_о

В зависимости от величины магнитной проницаемости все вещества (их можно называть магнетиками) делятся на слабые, у которых магнитная проницаемость незначительно отличается от единицы, и сильные, у которых магнитная проницаемость много больше единицы.

Слабые магнетики, в свою очередь, делят на:

- диамагнетики, у которых магнитная проницаемость чуть меньше единицы и

- парамагнетики, у которых магнитная проницаемость чуть больше единицы.

При помещении вещества в магнитное поле оно, взаимодействуя с ним, "откликается" созда­нием собственного магнитного поля (то есть намагничи­вается). В слабых магнетиках собственное магнитное поле много меньше внешнего магнитного поля, и, в результате, суммарное магнитное поле в веществе незначительно отличается от внешнего (в отсутствии вещества).

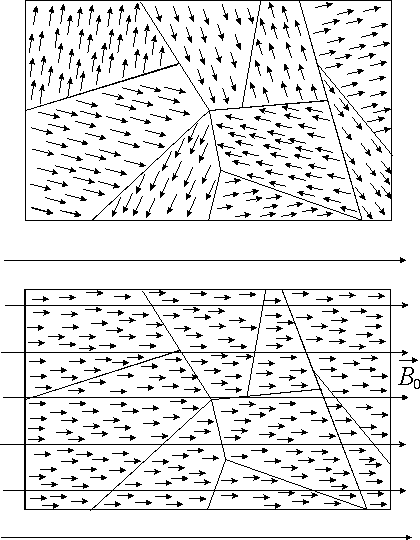
В диамагнетиках собственное магнитное поле, возникающее в результате взаимодействия вещества с внешним магнитным полем, направлено против внешнего поля, и в результате суммарное магнитное поле в диамагнетике меньше, чем в вакууме. Это соответствует значениям магнитной проницаемости меньшим единицы. У таких характерных диамагнетиков, как висмут, медь, вода, она составляет соответственно: 0,9996; 0,9999; 0,99999.

Также, как и поляризация диэлектриков внешним электрическим полем, намагничивание магнетиков может осуществляться двумя основными способами, механизмами - деформационным и ориентаци­онным. В результате того и другого способа образец ве­щества приобретает ненулевой результирующий магнитный момент.

Мерой намагниченного состояния вещества выбирается величина , называемая намагниченностью, численно равная магнитному моменту единицы объёма вещества: = /V, где - магнитный момент  - го атома вещества, а  и V - общее число атомов вещества и его полный объём, соответственно.

Диамагнетизм в чистом виде наблюдается у веществ, атомы которых в отсутствие внешнего магнитного поля обладают нулевым результирующим ма­гнитным моментом. Объяснение механизму взаимокомпенсации магнитных моментов совокупности электронов, входящих в атом, даёт кванто­вая механика.

Д

иамагнетизм связан с тем, что электрон в атоме является не просто носителем магнитного момента, то есть магнитной стрелкой, но, и обладает механическим моментом (моментом импульса ), то есть, представляет собой как бы волчок или гироскоп. И при включении внешнего магнитного поля, которое пытается повернуть магнитный момент электрона в своём направлении, характер вращательного движения электрона становится прецессирующим, то есть ось вращения электрона, сама начинает вращаться вокруг направления индукции внешнего поля. Такая прецессия (еще ее называют ларморовой прецессией) сопровождает­ся появле­нием дополнительного магнитного момента Р_м электрона, направленного против внешнего магнитного поля. Иначе, механизм диамагнетизма можно в классических терминах истолковать и как индуциро­вание включаемым внешним магнитным полем токов и связанных с ними магнитных моментов электронов, направленных по правилу Ленца так, чтобы противодействовать причине их вызвавшей. В итоге, в диамагнетике создается собственное маг­нитное поле, направленное против внешнего и ослабляющее внешнее магнитное поле внутри диамагнетика. Схематически это можно изобразить так.

В = _оН = В_о - В^; В^ = _оJ; В = _о(Н - J);  = ВВ_о = 1 – В^В_о = 1 – JН

Индуцированные внеш­ним магнитным полем магнит­ные моменты электронов и в целом намагни­ченность диамагнети­ка практически не зависят от температуры, что отличает диамаг­не­тизм от пара- и ферромагнетизма.

У ряда веществ, атомы которых обладают ненулевым магнитным моментом в отсутствие внешнего магнитного поля, диамагнитный эффект перекрывается и маскируется более сильным парамагнитным эффектом. К таким веществам относят вещества с нечётным числом электронов, например алюминий, щело­чные металлы, вольфрам и другие. Магнитная проницаемость у парамаг­нети­ков незначительно (на доли процента) больше единицы. У наиболее сильного парамагнетика - жидкого кислорода магнитная проницаемость равна 1,0034.

П

арамагнетики являются магнитными аналогами полярных диэлектриков, и механизм их намагничивания носит ориентационный характер. При помещении во внешнее магнитное поле на магнитные моменты атомов действует со стороны магнитного поля вращающий момент, который и поворачивает, ориентирует их в направлении индукции внешнего поля. В результате образец пара­магнетика намагничивается в направлении внешнего магнитного поля, то есть его собственное магнитное поле направлено так же как внешнее, и суммарное магнитное поле в веществе больше, чем в вакууме. Ориентирующему действию внешнего магнитного поля препятствует разупорядочи­вающее действие хаотического теплового движения. В результате действия этих противонаправлен­ных факторов достигается некоторое динамическое равновесие, которое смещается в ту или иную сторону при увеличении либо температуры, либо ин­дукции внешнего магнитного поля.

Схематически механизм намагничения парамагнетика представлен на рис.

В = _оН = В_о + В^; В^ = _оJ; В = _о(Н + J);  = ВВ_о = 1 + В^В_о = 1 + JН

Ферромагнетики. Домены и спиновая природа ферромагнетизма. Кривая намагничивания и магнитный гистерезис. Точка Кюри.

Ферромагнетики явились исторически первыми изученными представителями сильных магнетиков. К ним относят железо, кобальт, никель, гадолиний. Магнитная проницаемость у этих веществ составляет сотни и тысячи, то есть в них под действием внешнего магнитного поля возни­кает сильное соб­ственное магнитное поле, сонаправленное внешнему магнитному полю и много­кратно усиливаю­щее его. Природа ферромагнетизма долгое время оставалась загадкой и тай­ной для физиков, которая была раскрыта лишь в нашем столетии после соз­дания квантовой механики, вскрывшей специфические законы движения и вза­имодействия микрообъектов во внутриатомных масштабах.

В некоторых веществах (к ним относят так называе­мые переходные металлы) энергетически выгод­ной при не очень высоких температурах оказы­вается параллельная ориентация собст­венных (спи­но­вых) магнитных моментов в пре­делах отдельных макроскопических областей образца, назы­ваемых доменами.

В отсутствие внешнего магнитного поля образец ферромагнетика под действием теплового движения обычно оказывается размагни­ченным, то есть нама­гниченность в разных доменах ориенти­рована случайным образом и по всему образцу оказывается равной нулю. Внутри же каждого домена образец намагничен до насыщения и обладает значи­тельным магнитным моментом. Поэтому, пpи нало­жении внешнего магнитного поля на каждый домен действует большой вращающий момент, стремящийся сориентировать магнитный момент домена в на­п

равлении внешнего магнитного поля. Внешнее магнитное поле ориен­тирует домены (а не отдельные атомы) по полю, и уже в малых полях результи­рующее магнитное поле В быстро растет с рос­том внешнего магнитного поля (участок 1 - 2) достигая насыщения, когда все домены развернулись по полю. При уменьшении поля до нуля (точка 3) ферро­магнетик остается частично намагни­ченным, т. к. тепло­вое движение не в состоянии быстро развернуть такие круп­ные образования. Свойство ферромагнетика оста­ваться частично намагничен­ным используется для полу­чения постоянных магнитов. Чтобы пол­ностью размаг­нитить ферромагнетик необходимо дополнительное поле обратного направления (точка 4). Дальнейшее увеличение поля приводит к перемагничиванию (участок 4 - 5). Затем фер­ромагнетик можно размагнитить (5 – 6 - 7) и пе­ремагнитить до насыщения (7 - 2). Эта кривая на­зывается петлей гис­терезиса.

Для каждого ферромагнетика имеется оп­ределенная температура, называемая точкой Кюри, при которой области спонтанного намаг­ничения распадаются, и вещество утрачивает ферромагнитные свойства.

Из сказанного ясно, что магнитная проницаемость  для диа- и парамагнетиков при изменении внешнего магнитного поля остается неизменной. У ферромагнетиков магнитная проницаемость сильно зависит от величины внешнего магнитного поля.

С ростом индукции (напряжённости) внешнего магнитного поля намагниченность образца ферромагнетика растёт нелинейным образом и достигает состояния насыще­ния. Кривая, изображающая зависимость J(Н), называемая кривой намагничива­ния, изобра­жена на рис.

Н

На этой кривой выделяют три участка. На первом участке намагниченность растёт не очень быстро. Здесь происходит рост так называемых "выгодно ориентированных" доменов, магнитные моменты которых близки по направле­нию к индукции внешнего магнитного поля, за счёт «невы­годно» ориентиро­ванных доменов. На втором участке кривой намагничивания внешнее магнитное поле становится достаточно сильным для поворотов, пе­реориентации "невыгод­ных доменов" в целом в своем направлении. Здесь имеет место скачкообразная переориентация магнитных моментов целых доменов. С этими скачками в изменении магнитного момента образца (его намагничен­ности), называемыми скачками Баркгаузена, связаны звуковые эффекты в виде треска, щелчков в наушниках, подключенных к образцу ферромагнетика.

Н

а третьем участке достигается насыщение: все домены сориентировали свои магнитные моменты в направлении внешнего магнитного поля.

Схематически намагничение ферромагнетика представлено на рисунке. Зависимость индук­ции результирующего магнит­ного поля в ферро­магнетике от напряженно­сти внешнего поля так же, как и кривая намагничи­ва­ния, носит нелинейный и неоднозначный харак­тер. Если образец ферромаг­нетика первоначально был размагничен, то зависи­мость В (Н) имеет вид, пред­ставленный на рис.

С ростом напряжённости внешнего магнит­ного поля индукция результирующего маг­нитного поля в ферромагнетике нелинейно растёт вплоть до участка насыщения. Если же затем напря­жённость внешнего поля уменьшить до нуля, индукция результирующего магнитного поля не уменьшится до нуля, а сохранит некоторое значение В_ост, называемое остаточной индукцией. Это явле­ние интерпретируется как магнитная вязкость; часть доменов как бы вязнет, застревает в своей предыдущей ориентированности сильным внешним магнитным полем. Теплового же движения оказывается недостаточно для полной разориентации доменов и для размагничивания образца ферро­магнетика. Такой образец представляет собой постоянный магнит. Размагнитить его можно либо меха­нической встряской (ударом), либо тепловой, то есть нагревом до значительной температуры, либо жеприложением внешнего поля, противоположного первоначальному направления. Величина соответствующей напряжённости Н_с (см, рис.) называется коэрцитивной силой.

Если напряжённость внешнего магнитного поля циклически менять в значительных пределах, при которых достигается состояние насыщения (все домены сориентировали свои магнитные моменты в направлении внешнего магнитного поля), то зависимость В(Н) изображается замкнутой петлеобразной кривой, называемой петлей гистерезиса.

Ферромагнитное состояние, то есть самопроизво- льная, спонтанная copиентированность маг­нитных моментов всех атомов в пределах домена, сохра­няется лишь в определённом диапазоне тем­пе­ратур, ограниченном сверху температурой Т_с, назы­вае­мой температурой Кюри. При этой температуре теп­ловое разупорядочивающее движение атомов ста­новится столь интенсивным, что превышает упорядо­чивающее действие квантовомеханических, так назы­вемых обменных сил, и домены распадаются на разу­порядоченные атомы; ферро­магнетик превращается в парамагнетик: Т_{с Fе} = 1040 К, Т_{с Со} = 730 К.

Лекция 13. Обобщение Максвеллом представлений об электромагнитной индукции. Взаимосвязь переменных электрического и магнитного полей. Уравнения Максвелла в интегральной и дифференциальной формах, их физическое истолкование Сравнительная характеристика электрического и магнитного полей.

Про классическую теорию электромагнитного взаимодействия и его переносчика - электро­магнитное поле - говорят иногда, что электродинамика Максвелла - это уравнения Максвелла. В 60 - ых годах прошлого столетия Максвелл выполнил работу, подобную той, которую два века до него осуществил Ньютон. Если Ньютон довершил создание первой фунда­ментальной теории движения, то Максвелл завершил создание первой теории физического взаимо­действия (электромагнит­ного). Подобно классической механике Ньютона, в основу электродина­мики Максвелла также были положены некоторые предельно фундаментальные и элеме­нтарные соотношения, выраженные уравнениями, получившими имя Максвелла.

Эти уравнения имеют две формы - интегральную и дифференциальную своего выражения и фактически они выражают взаимосвязь характеристик электромаг­нитного поля с характеристи­ками источников (зарядов и токов), это поле по­рождающих. Эта связь не имеет такого простого выражения, как, например связь мер движения и взаимодействия, выражаемая основным законом динамики - вторым законом Ньютона. Поэтому уравнения Максвелла, выражающие основную идею электродинамики - учения об электромагнитном взаимодействии - появ­ляются при её изучении в вузе - лишь в конце курса.

Как и любые другие предельно общие теоретические положения, уравнения Максвелла в рамках самой электродинамики формально не выводятся. Они получаются как результат творче­ского обобщения разнообразного опытно-экспери­ментального материала, и их правильность подтверждается различными следс­твиями и практическими приложениями.

До Максвелла была известна полная система уравнений электро- и магнито­статики и одно уравнение электродинамики - уравнение, выражающее закон электромагнитной индукции. В целом же эта совокупность уравнений не явля­лась полной системой, однозначно задающей состояние элек­тромагнитного по­ля. Для получения такой системы Максвелл произвёл обобщение закона элект­ро­магнитной индукции  = - dФdt, записав его уравнение в интегральной форме:

= - = - (вектор зависит и от t, и от , а поток Ф = - только от t)

Полученное уравнение можно представлять себе как обобщённую на вихре­вое электрическое поле, теорему о циркуляции вектора в электростатике. Здесь Максвелл фак­тически выбросил проводящий контур, который был у Фарадея и который, по Максвеллу, являлся просто индикатором наличия (по индук­ционным токам) вихревого электрического поля в области вокруг изменяющегося магнитного поля.

В представленной Максвеллом форме закона электромагнитной индукции более выпукло просвечивает физическая суть явления, согласно которому переменное магнитное поле порождает в окружающем пространстве вихревое (с ненулевой циркуляцией) электрическое поле. Представив так явление электромагнитной индукции, Максвелл смог, опе­ревшись на соображения симметрии, пред­положить возможность существования в природе и обрат­ного электромагнитной индукции эффекта. Его можно назвать магнитоэле­ктрической индукцией, суть которой в том, что изменяющееся во времени элект­рическое поле, порождает в окружающем пространстве магнитное поле. Формально это записыва­ется так, что циркуляция напряженности магнитного поля равна быстроте изменения во времени потока индукции электрического поля. С учётом же то­го, что магнитное поле с самого начала (со статического состояния) являе­тся вихревым, то есть для него циркуляция всегда не равна нулю, обоб­щённая взаимосвязь магнитного и электрического полей примет вид:

=  + _см, где _см =

З

десь быстрота изменения потока индукции электрического поля формально эквивалентна некоторому току. Этот ток называют током смещения. Можно пре­дставить, что этот ток как бы замыкает протекание тока в цепи, например, с конденсаторами, через которые обычный ток прово­димости не протекает. Плотность тока смещения равна быстроте изменения электрического смещения (вектора ): = ( /t). При разряде заряженного конденсатора по проводам протекает ток проводимости, и, кроме того, в пространстве между пластинами убывает (изменяется) электрическое поле.

Быстрота же изменения индукции электрического поля, то есть  t и есть плотность тока смещения . Ток смещения замыкает ток проводимости в разрывах между проводниками. Он, как и ток проводимости, создаёт вокруг себя магнитное поле, а в диэлектрике (там его называют поляри­зационным то­ком) он выделяет тепло - так называемые диэлектрические потери.

Итак, теперь мы можем записать полную систему уравнений единого элек­тромагнитного поля - систему уравнений Максвелла:

= - =  +

= q_ = 0

В статическом состоянии электрическое (электростатическое) поле порождается только неподвижными (или равномерно движущимися) в данной ИСО электрическими зарядами и является потенциаль­ным (обладает нулевой циркуляцией). Магнитостатическое поле порождается только токами и всегда является непотенциальным (вихревым). Электростатическое поле, имея своими источниками заряды, имеет начало своих сило­вых линий на положительных зарядах и конец - на отрицательных зарядах (или в бесконечности). Магнитное же поле не имеет таких источников, поскольку магнитных монополей до сих пор не обнаружено, и потому его силовые линии даже в статическом состоянии являются замкнутыми, не имея ни начала, ни конца.

В динамическом же, нестационарном состоянии, когда источники полей и сами, порождаемые ими поля, становятся изменяющимися во времени, выявляется новая принципиа­льная особенность электриче­ского и магнитного нестационарных полей. Выясняется, что в этом состоянии они приобретают способность порождать друг друга, становиться источниками друг друга. В результате возни­кает новое нераз­рывно взаимосвязанное состояние единого электромагнитного поля. Первое урав­нение Максвелла, как уже говорилось, указывает на то, что изме­няющееся во времени магнитное поле, порождает в окружающем пространстве вихревое электрическое поле. Второе же уравнение Максвелла говорит о том, что магнитное поле порождается не только токами, но и переменным во времени электрическим полем. В итоге мы можем заключить, что переменные (нестацио­нарные) электрическое и магнитное поля являются взаимными источниками друг друга, и их различие во многом относительно. В нестационарном состоя­нии они способны существовать совершенно само­стоятельно от источников (пе­ременных токов), их породивших, в виде единого неразрывного элек­тромагнитно­го поля.

Последние два уравнения Максвелла указывают на разный характер симметрии электриче­ского и магнитного стационарных полей.

Для решения основной задачи электродинамики, уравнения Максвелла, выра­жающие её основную идею (связь характеристик поля с характеристиками его источников), должны быть дополнены так называемыми материальными уравнения­ми, связывающими характеристики поля с характеристиками вещественной среды. Этими уравнениями являются следующие:

= _о ; = _о и =  , где  и  - диэлектрическая и магнитная проницаемости среды, а  - удельная электропроводность среды.

У

равнения Максвелла часто записывают в более компактной - дифференциа­льной форме, которая получается из интегральной формы путём предельного перехода контуров и поверхностей интегрирования к нулю: S  0 и L  0.

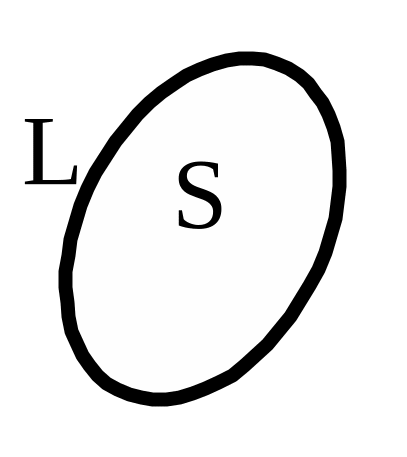
Введем векторный оператор, называемый "набла" и обозначаемый , как век­тор со следую­щими компонентами:  = (/х, /у, /z).

Для любого векторного поля ( ) = (А_х, А_у, А_z) важными являются следующие совокупно­сти дифференциальных операций:

а) скалярная, называемая дивергенцией :  = di = А_х/х + А_у/у + А_z/z

б) векторная, называемая ротором :

 = rot = (А_у/_z - А_я/_у) + (А_z/х - А_х/_z) + (А_у/_Х - А_Х/_У)

В этих обозначениях уравнения Максвелла в дифференциальной форме, примут следующий вид:

rot = -  /t ; rot = +  /t; di = ; di = 0

или  = -  /t ;  = +  /t;  = ;  = 0

В уравнения Максвелла входят только свободные заряды  и токи проводи­мости . Связан­ные заряды и молекулярные токи входят в эти уравнения неявно - через характеристики среды – диэлектрическую и магнитную проницаемости  и .

Для перехода к дифференциальной форме записи теоремы о циркуляции воспользуемся известной из векторного анализа теоремой Стокса, связывающей циркуляцию вектора с поверхностным интегралом от ротора этого вектора:

= ,

где S – поверхность, ограниченная контуром L. Под ротором вектора понимают векторный дифференциальный оператор, задаваемый следующим образом:

rot = (Е_у/z - Е_z/у) + (Е_z/х - Е_х/z) + (Е_x/y - Е_y/x)

Физический смысл ротора вскрывают, устремляя поверхность S к нулю. В пределах достаточно малой поверх­ности ротор вектора можно считать постоянным и вынести за знак интеграла:

= rot  = rot S.

Тогда, согласно теореме Стокса: rot = (1S) при S  0.

Отсюда ротор вектора можно определить как поверхност­ную плотность циркуляции этого вектора.

Так как в ЭСП циркуляция вектора равна нулю, то равен нулю и ротор вектора :

rot = 0.

Это уравнение и есть дифференциальная форма теоремы о циркуляции вектора в ЭСП.

Для перехода к дифференциальной форме записи теоремы Остроградского – Гаусса воспользуемся известной из векторного анализа теоремой Гаусса, связывающей поток вектора по замкнутой поверхности с интегралом от дивер­генции этого вектора по объему, заключенному в этой поверхности:

=

Под дивергенцией вектора понимают скалярный дифференциальный оператор (совокупность производных), задаваемый следующим образом:

div = Е_х/х + Е_у/у + Е_z/z.

Физический смысл дивергенции вскрывают, устремляя объем V к нулю. В пределах достаточно малого объема дивергенцию вектора можно считать постоянной и вынести за знак интеграла:

= div  = (1V) div . Тогда, согласно теореме Гаусса,

div = (1V) при V  0.

Отсюда дивергенцию вектора можно определить как объемную плотность потока этого вектора.

Соотнося теорему Остроградского – Гаусса = q_/_о = (1_о) и теорему Гаусса = , видим, что левые их части равны друг другу. Приравнивая их правые части, получаем:

div = _о.

Это уравнение и представляет собой дифференциальную форму теоремы Остроградского – Гаусса.

Лекция 14. Электромагнитные волны. Объяснение возникновения электромагнит­ных волн с позиций уравнений Максвелла. Уравнение бегущей электромагнитной волны. Волно­вое уравнение. Перенос энергии электромагнитной волной. Вектор Умова - Пойнтинга. Излучение диполя.

Электромагнитные волны представляют собой распространяющиеся в простра­нстве взаимо­связанные колебания электрического и магнитного полей. В отли­чие от звуковых (акустических) волн, электромагнитные волны могут распро­страняться в вакууме.

Качественно механизм возникновения свободного (от источников в виде электрических зарядов и токов) электромагнитного поля может быть пояснён на основе анализа физической сущности уравнений Максвелла. Два фундамента­льных эффекта, отображаемых уравнениями Максвелла - электромагнитная инду­кция (порождение переменным магнитным полем переменного вихревого электри­ческого поля) и магни­тоэлектрическая индукция (порождение переменным элек­трическим полем переменного магнит­ного поля) приводят к возможности эле­ктрического и магнитного переменных полей быть взаимными источниками друг друга. Взаимосвязанное изменение электрического и магнитного полей и пре­дставляет собой единое электромагнитное поле, которое способно в вакууме распро­страняться со скоростью света с = 310⁸ м/с. Это поле, способное существовать совершенно незави­симо от зарядов и токов и вообще от вещества и представляет собой второй (на­ряду с веществом) - полевой вид (форму) существования материи.

В опыте электромагнитные волны были обнаружены в 1886 г Г. Герцем, спустя 10 лет после смерти, предсказавшего теоретически их существование Максвелла. Из уравнений Максвелла в непроводящей среде, где  = 0 и = 0, взяв операцию ротора от первого уравнения и подставив в него выражение для rot из второго уравнения, получим:

rot = -  /t = - _о /t; rot rot = -_о/t(rot ) = - _о_о ²/t² = - (1/²)Е²/t² rot =  /t = _о  /t;

Из векторного анализа известно, что rot rot = grad div –  , но grad div  0 и тогда

 = 1/²) ²/t² , где  = ²/х² + ²/у² + ²/z² - оператор Лапласа - сумма вторых частных производных по пространственным координатам.

В одномерном случае получаем дифференциальное уравнение в частных производных, называемое волновым:

 ²/х² - 1/²) ²/t² = 0

Такого же типа уравнение получается и для индукции магнитного поля. Его решением является бе­гущая плоская монохроматическая волна, задавемая уравнением:

= cos (t – kх + ) и = cos (t – kх + ) , где /k =  = 1/(_о_о) - фазовая скорость волны.

В

екторы и изменяются синфазно во времени, но во взаимно перпенди­кулярных плоскостях и перпендикулярно направлению распространения (скорости волны):  ,  ,  .

Свойство взаимоперпендикулярности векторов и и и позволяет отнести электромагнит­ную волну к поперечным волнам.

В вакууме электромагнитная волна распространяется со скоростью света  = с = 1/(_о_о) = 310⁸ м/с, а в вещественной среде волна замедляется, ее скорость убывает в () раз, то есть  = с/() = 1/(_о_о).

В каждой точке пространства значения векторов и пропорциональны друг другу. Отношение напряжённостей электрического и магнитного полей определяется электрическими и магнитными свойствами (проницаемостями  и ) среды. Это выражение связано с равенством объемных плотностей энергий _э и _м электрического и магнитного полей волны:

_э = _оЕ²/2 = _м = _оН²/2  Е/Н = (_о/_о).

Отношение Е/Н, как нетруд­но видеть, имеет размерность сопротивления: В/м : А/м = В/А = Ом. Применительно к вакууму, например, Е/Н = (_о/_о) = 377 Ом - называется волновым сопро­тивлением вакуума. Отношение же Е/В = 1(_о_о) = с = 310⁸ м/с (в вакууме).

Распространя­ющиеся в пространстве электромагнитные колебания (электромагнитные волны) переносят энергию без переноса вещества - энергию электрического и магнит­ного полей. Ранее мы получали выражения для объёмных плотностей энергии электрического и магнитного полей:

_э = _оЕ²/2 и _м = _оН²2 [Дж /м³].

Основной характеристикой переноса энергии волной является вектор пло­тности потока энергии, называемый (применительно к электромагнитным волнам) вектором Пойнтинга, численно равный энергии, переносимой через единицу пло­щади поверхности нормальной к направлению распространения волны, за единицу времени:   = Дж/м²с = Вт/м².

За единицу времени через единичную площадку пройдёт вся та энергия, ко­торая содержится в объеме V параллелепипеда (цилиндра) с основанием в 1 м² и высотой равной скорости  распростра­нения волны, то есть пути, проходимому волной за единицу времени:

S = V =  = (_э + _м)(_о_о) = _оЕ²2(_о_о) + _оН²2(_о_о) = [(_о _о)]Е²/2 + [(_о _о)] Н²/2.

Так как Е/Н = (_о/_о), то S = ЕН/2 + НЕ/2 = ЕН.

В векторной форме вектор Пойнтинга выразится как произведение векторов напряженностей электрического и магнитного полей: = [ ] =  .

Простейшим излучателем электромагнитных волн служит электрический диполь, момент которого изменяется с течением времени. Если изменения электри­ческого момента носят повто­ряющийся, периодический характер, то такой "ко­леблющийся диполь" называется осциллятором или элементарным вибратором. Он представляет собой простейшую (элементарную) модель излу­чательной сис­темы в электродинамике. Любой электронейтральный излучатель с размерами L   в так называемой волновой или дальней зоне (при r   ) имеет та­кое же поле (характер распреде­ления в пространстве) излучения, как и ос­циллятор с равным дипольным моментом.

О

сциллятор называют линейным или гармони- ческим, если у него дипольный момент изменяется по гармониче­скому закону: Р = Р_м sin t; Р_м = ql.

Как показывает теория излучения, мгновенная мощность N излучения элек­тромагнитных волн гармони­ческим осциллятором пропорциональна квадрату вто­рой производной изменения его дипольного момента, то есть:

  d²Рdt²²;  = _оd²Рdt²²6с = _о⁴Р_м²sin² t6с.

Средняя мощноcть    излучения диполя за период колебаний равна:

   = (1Т)  dt = _о⁴Р_м²12с

Обращает на себя внимание четвертая степень частоты в формуле для мощности излучения. Во многом поэтому для передачи радио- и телеинформации используются высокочастотные несущие сигналы.

Диполь излучает неодинаково в различных направлениях. В волновой (дальней) зоне интен­сивность J излучения диполя: J  sin²  r² , где  - угол между осью диполя и направлением излу­чения. Зависимость J () при фиксированном r называется полярной диаграммой направленности излучения диполя. Она имеет вид восьмёрки. Из неё видно, что диполь сильнее всего излучает в направлении  = /2, то есть в плоскости перпендикулярной оси диполя. Вдоль собственной оси, то есть при  = 0 или  = , диполь совершенно не излучает электромагнитные волны.

Лекция 15. Взаимодействие электромагнитных волн с веществом. Фазовая и групповая скорости электромагнитных волн. Нормальная и аномаль­ная дисперсии. Электронная теория дисперсии.

Уравнение бегущей монохроматической волны Е = Е_м cos (t – kх + ) является идеализа­цией реального волнового процесса. В действительности ему должна соответствовать бесконечная во времени и пространстве последовате­льность горбов и впадин, перемещающаяся в положитель­ном направлении оси х со скоростью  = /k. Эта скорость называется фазовой, ибо представляет собой быстроту перемещения в пространстве эквифазовой поверхности (поверх­ности постоянной фазы). Действительно, уравнение эквифазовой поверхности имеет вид: Ф = (t – kх + ) = const или, иначе, dФ = 0, то есть dt - kdх = 0, откуда dх/dt =  = /k.

Реальные волновые процессы ограничены во времени, то есть имеют начало и конец, и у них меняется амплитуда. Их аналитическое выражение может быть представлено в виде набора, группы, пакета волн (монохроматических):

Е = Е_{м } cos (t – k_ х + _)d

с близкими частотами, лежащими в узком интервале от  - /2 до  + /2, где    и близ­кими (не сильно различающимися) спектральными плотностями амплитуды Е_{м }, волновыми числами k_ и начальными фазами _.

При распространении в вакууме волны любой частоты имеют одинаковую фазовую ско­рость  = с = 1(_о_о) = 310⁸ м/с, равную скорости света. В вещественной среде за счёт взаимодействия электромагнитной волны с заряженными частицами (электронами прежде всего) скорость распространения волн начинает зависеть от свойств среды, её диэлектрической, и магнитной проницаемостей, согласно формуле:  = 1/(_о_о).

Диэлектрическая и магнитная проницаемости вещества оказываются зави­сящими от частоты (длины) электромагнитной волны, а, следо­вательно, и фазовая скорость распро­странения волны в веществе оказывается разной для разных её частот (длин волн). Этот эффект называется дисперсией электромагнитных волн, а среды называют диспергирующими. Веществен­ная среда может быть не диспергирующей лишь в некотором, не очень широком диапазоне частот. Совершенно не диспергирующей средой является лишь вакуум.

При распространении в диспергирующей среде волнового пакета, составляю­щие его волны с различающимися частотами будут обладать различными скорос­тями и с течением времени будут "разъезжаться" друг относительно друга. Волновой пакет будет в такой среде постепенно расплываться, рассеиваться, что и отражается термином "дисперсия".

Для характеристики скорости распространения волнового пакета как це­лого принимают скорость распространения его максимума - центра пакета волн с наибольшей амплитудой. Эту скорость называют групповой и, в отличие от фазовой скорости  = /k, она определяется не через отношение /k, а через производную u = d/dk.

Естественно, что в вакууме, то есть в отсутствие дисперсии, фазовая ско­рость (быстрота переме­щения эквифазовой поверхности) и групповая (быстрота переноса энергии волной) совпа­дают и равны скорости света. Понятие групповой скорости, определяемое через производную (быстроту изменения угловой часто­ты с ростом волнового числа) применимо только для несильно дисперги­рующих сред, где не очень сильное поглощение электромагнитных волн. Получим фор­мулу взаи­мосвязи групповой и фазовой скоростей:

u = d/dk =  - (k/k)d/d =  - d/d.

В зависимости от знака производной d/d, групповая скорость u =  - d/d может быть как меньше, так и больше фазовой скорости  электромагнитной волны в среде.

В отсутствие дисперсии d/d = 0, и групповая скорость равна фазовой. При положительной производной d/d  0, групповая скорость меньше фазовой, имеем случай, называемый нормаль­ной дисперсией. При d/d  0, групповая скорость волн больше фазовой: u  , этот слу­чай дисперсии называют аномальной дисперсией.

Причины и механизм явления дисперсии просто и наглядно можно проиллюстри­ровать на примере прохождения электромагнитной волны через диэлектрическую среду. В ней переменное электрическое поле взаимодействует со связанными в атомах вещества внешними электронами. Напряжённость электрического поля электромагнитной волны играет для электрона роль периоди­ческой вынуждающей силы, навязывающей ему вынужденное колебательное движение. Как мы уже ана­лизировали, амплитуда вынужденных колебаний зависит от частоты выну­ждающей силы, и в этом и кроются причины дисперсии электромагнитных волн в веществе и зави­симости диэлектрической проницаемости вещества от частоты электромагнитной волны.

При смещении электрона, связанного с атомом, на расстояние х от положения равновесия, атом прибретает дипольный момент р = q_ех, а образец в целом - есть макродиполь с поляризованностью Р = nр = nq_еx, где n - число атомов в единице объёма, q_е – заряд электрона.

Из связи векторов и можно выразить диэлектрическую восприимчивость , проницаемость , а затем скорость  электромагнитной волны в веществе:

Р = _оЕ = nq_ех   = nq_ех_оЕ;  = 1 +  = 1 + nq_ех_оЕ;  = с()  с (при   1). Для небольших х:  = с/(1 + nq_ех_оЕ)  с/(1 + nq_ех2_оЕ).

Отталкиваясь от второго закона Ньютона для упруго связанного с атомом электрона, находящегося в возмущающем электрическом поле Е = Е_мcos t электромаг­нитной волны, найдём его смещение х от положения равновесия в атоме. Полагаем, что смещение х электрона изменяется по закону вынуждающей силы, то есть х = Х_мсоs t.

ma = - kх – r + F_вын; mх^ = - kх – rх^ + q_еЕ, или, при r = 0  х^ + _о²х = q_еЕ_мcos tm,

где _о² = km – собственная частота колебаний электрона, упруго связанного с атомом.

Подставляем решение х = Х_мсоs t в полученное дифференциальное уравнение вынужденных колебаний электрона:

- ²х + _о²х = q_еЕ_м cos tm  х = q_еЕ_м cos t[m(_о² - ²)] = q_еЕ[m(_о² - ²)]

Подставляем полученное выражение для смещения х в формулу для фазовой скорости электромагнитной волны:

  с/(1 + nq_ех2_оЕ) = с[1 + nq_е²2m_о(_о² - ²)]

На частоте  = _о фазовая скорость  электромагнитной волны обращается в ноль.

На некоторой частоте _р, при которой nq_е²m_о(_о² - _р²) = - 1, фазовая скорость волны претерпевает разрыв. Значение этой «резонансной» частоты _р = _о + nq_е²m_о  10¹⁷ с^-1.

Изобразим полученную зависимость фазовой скорости от частоты и от длины волны. Разрывный характер зависимости (), называемой дисперсионной, связан с тем, что мы пренебрегли сопротивлением среды и диссипа­цией энергии колебаний, положив коэффициент сопротивления r = 0. Учет трения приводит к сглаживанию дисперсионной кривой и устранению разрывов.

Т

ак как частота  и длина волны  обратно пропорциональны ( = 2 = 2с/), то график дисперсионной зависимости () обратен графику ().

На участке нормальной дисперсии 1 - 2 фазовая скорость  больше скорости света в вакууме. Это не противоречит теории относительности, ибо реальный сигнал (информация, энергия) передаются с групповой скоростью u, которая здесь меньше скорости света.

Групповая скорость u =  - d/d превышает скорость света с в вакууме на участке аномальной дисперсии 2 – 3, где фазовая скорость  убывает с ростом длины волны  и производная d/d  0. Но в области аномальной дисперсии имеет место сильное поглощение, и понятие групповой скорости становится неприменимым.

Лекция 16. Представления о пространстве и времени в современной физике. Объединение пространства со временем в СТО. Относительность классических понятий одновременности, длины и длительности.

В 1905 г А. Эйнштейн впервые оформил в теоретическую систему кинематические, т. е. простран­ственно-временные представления, «подсказанные» опытом анализа движений с большими, так называемыми релятивистскими (соизмери­мыми со скоростью света с = 310⁸ м/с в вакууме) скоростями.

В механике Ньютона пространственно-временные представления специ­ально не выделялись и фактически считались очевидными, согласующимися с наглядным опытом медленных движений. Однако предпринятые в XIX в попытки объяснить исходя из этих представлений особенности распространения такого релятивистского объекта как свет, приводили к противоречию с опытом (опыт Майкельсона, 1881 г, 1887 г. и др.). Анализируя возникшую проблемную ситуацию, А. Эйнш­тейн сумел в 1905 г сформулировать два основополагающих утверждения, на­зываемых постулатами (принципами), согласующихся с опытом релятивистских (высокоскоростных) движений. Эти утверждения, получившие название посту­латов Эйнштейна, составили основу его специальной (частной) теории отно­сительности.

1. Принцип относительности Эйнштейна: все законы физики инвариантны по отношению к выбору инерциальной системы отсчета (ИСО), т. е. в любых ИСО законы физики имеют одинаковый вид, не зависят от произвола субъекта (ученого) в выборе ИСО. Или, иначе - все ИСО равноправны, отсутствует какая-либо привилегированная, избранная, абсолютная⁵ ИСО. Или, еще - никакими физи­ческими опытами, проводимыми внутри ИСО, нельзя определить, движется она с постоянной скоростью или покоится. Этот принцип согласуется с принципом объективности познания.

До Эйнштейна в механике был известен принцип относительности Галилея, который был ограничен рамками только механических явлений и законов. Эйнштейн фактически обобщил его на любые физические явления и законы.

2. Принцип инвариантности (постоянства) и предельности скорости света. Скорость света в вакууме конечна, одинакова во всех ИСО, т. е. не зависит от относительного движения источ­ника и приемника света и является преде­льной скоростью передачи взаимодействий. Этот принцип закреплял в физике концепцию близкодействия, сменившую господствовавшую ранее концепцию дальнодействия, основывающуюся на гипотезе о мгновенности передачи взаимо­действий.

И

з двух принципов (постулатов) Эйнштейна вытекают важнейшие для кинематики, более общие, чем классические (галилеевские) преобразования, то есть фор­мулы взаимосвязи пространственных и временной координат x, y, z, t одного и того же события⁶, наблюдаемого из разных ИСО.

Возьмем частный случай выбора двух ИСО, при котором одна из них, обозначае­мая (К), дви­жется относительно дру­гой, обозначаемой (К^), со скоростью V вдоль оси х. В начальный момент времени начала координат О и О^ обеих ИСО сов­падали, и оси Y и Y^, а также Z и Z^, тоже совпа­дали. Для этого случая формулы преобразова­ния пространственно-временных координат одного и того же события при переходе от одной ИСО к другой, назы­ваемые преобразованиями Лоренца, имеют следующий вид:

х^ = (х - Vt)(1 - V²с²); у^ = у; z^ = z; t^ = (t - Vхс²)(1 - V²с²) -

- прямые преобразования Лоренца (из ИСО (К) в ИСО (К^);

х = (х^ + Vt^)(1 - V²с²); у = у^; z = z^; t = (t^ + Vх^)(1 - V²с²) -

- обратные преобразования Лоренца (из ИСО (К^) в ИСО (К).

Преобразования Лоренца являются более общими, по сравнению с преобразованиями Галилея, которые они содержат в себе как частный, предельный случай, справедливый при малых, дорелятивистских скоростях (  с и V  с) движений тел и ИСО. При таких, «клас­сических» скоростях, (1 – V²с²)  1, и преобразования Лоренца переходят в преобразования Галилея: х^ = х - Vt; у^ = у; z^ = z; t^ = t и х = х^ + Vt^; у = у^; z = z^; t = t^

В таком соотношении формул преобразования Лоренца и Галилея находит свое проявле­ние важный методологический принцип научно-теоретического познания - принцип соответст­вия. Согласно принципу соответствия, научные теории диалектически развиваются по пути ступенчатого обобщения - расширения своей предметной области. При этом более общая теория не от­меняет прежнюю, частную, а лишь вскрывает ее ограниченность, очерчивает границы и пределы ее справедливости и применимости, и сама сводится к ней в области этих границ.

Термин "специальная" в названии теории относительности Эйнштейна озна­чает как раз, что она сама является ограниченной (частной) по отношению к другой, тоже созданной А. Эйнштейном теории, получавшей название "общая теория относительности". Она обобщает специальную теорию относительности на любые, не только инерциальные системы отсчета.

Из преобразований Лоренца вытекает ряд кинематических следствий, про­тиворечащих наглядным классическим представлениям и давшим основание назвать релятивистскую кине­матику и релятивистскую механику в целом теорией относительности.

Что же относительно, то есть, зависимо от выбора ИСО в СТО? Прежде всего, относи­тельным оказывается факт одновременности двух событий, а также длина тела и длительность процесса. В релятивистской динамике в разряд относительных переходит сила, а у некоторых ученых и масса. Следует, однако, помнить, что главным в любой теории является не относительное, а инвариантное (устойчивое, сох­раняющееся, неизменное). Релятивистская механика, вскрывая относительность одних понятий и величин, заменяет их другими инвари­антными величинами, такими, например, как комбинация (тензор) энергии-импульса.

1. Относительность одновременности собы­тий.

Пусть в ИСО (К) происходят два события, зада­ваемые координатами x_1, y_1, z₁, t₁ и x_2, y_2, z₂, t₂, причем t₁ = t_2, т. е. в ИСО (К) эти события происходят одно­временно.

Громадной заслугой Эйнштейна явилось привлечение внимания к тому, что в классической механике Галилея - Ньютона совершенно не было определе­но, как фиксиро­вать факт одновременности двух событий, находящихся в разных местах. Интуитивно, в соответствии с принципом дальнодействия, пред­полагающим бесконечной скорость распро­странения взаимодействий (что дос­таточно оправдано для медленных движений), считалось очевидным, что раз­несенность событий в пространстве не может влиять на характер их времен­ного соотношения. Э

йнштейн же предложил строгий способ установления фак­та одновремен­ности разноместных событий, основанный на размещении в этих местах синхронизированных часов. Синхронизировать часы он предложил с помощью реального сигнала, обладающего наивысшей скоростью - светового сигнала. Одним из способов синхронизации часов в конкретной ИСО является такой: часы, находящиеся в точке с координатой х будут синхронизированы с единым центром в точке 0 - начале ИСО, если в момент прихода к ним светового сигнала, испущенного из точки 0 в момент t_о, они покажут время t_х = t_о + х/c.

Так как синхронизация осуществляется сигналом, обладающим предельно высо­кой, но не бесконечной скоростью, то часы, синхро­низи­ро­ванные в одной ИСО, окажутся разсинхрони­зиро­ванными в другой (и во всех других) ИСО в силу их относительного движения. Следствием этого и является относительность одновременности разноместных событий и относительность временных и пространственных интерва­лов (длительностей и длин).

Формально этот вывод следующим образом вытекает из преобразований Лоренца: в ИСО (К^) событию 1 соответствует момент времени t₁^ = (t₁ - Vх₁с²)(1 - V²с²), а событию 2  момент t₂^ = (t₂ – Vх₂с²)(1 – V²с²), так, что при t₁ = t₂, t₂^ – t₁^ = [(х₁ – х₂)Vс²](1 – V²с²), и два события 1 и 2, одновременные в одной ИСО – в ИСО (К), оказываются неодновременными в другой (в ИСО (К^).

В классическом (дорелятивистском) пределе, при V  с, t₂^ – t₁^  0, факт одновременно­сти двух событий становится аб­солютным, что, как уже говорилось, соответствует бесконечной скорости передачи взаимодействий и синхронизирующего сигнала: с   или с  V.

В релятивистской теории одновременность событий оказывается абсолют­ной лишь в частном случае одноместных событий: при х₁ = х₂ всегда при t₁ = t₂ и t₁^ = t₂^.

2. Относительность длины тел (пространственных интервалов).

Пусть в ИСО (К) вдоль оси х покоится стержень длиной l_о = х₂ – х₁.

ИСО, в которой тело покоится, называется собственной для данного тела, а его характеристики, в данном случае длина стержня, также называются собственны­ми.

В ИСО (К^), относительно которой стержень движется, и которая называется лаборатор­ной ИСО, длина стержня l^ = х₂^ - х₁^ определяется как разность координат концов стержня, зафиксированных одновременно по часам данной ИСО, т. е., при t₁^ = t₂^.

Используя формулы преобразований Лоренца для х₁ и х₂, содержащие время в штрихованной ИСО (К^), установим взаимосвязь l и l^:

х₁ = (х₁^ + Vt₁^)(1 - V²с²); х₂ = (х₂^ + Vt₂^)(1 - V²с²);  х₂ - х₁ = (х₂^ - х₁^)(1 - V²с²)

или окончательно: l^ = l_о(1 - V²с²) – эта формула выражает закон прео­бразования длин (пространственных интервалов), согласно которому в на­правлении перемещения размеры тел сокращаются. Этот эффект относитель­ности длины тел, их релятивистского сокращения в направлении перемещения, является реальным, а не кажущимся физическим эффектом, но не динамичес­ким, не связанным с каким-либо силовым воздействием, вызывающем сжатие тел и сокращение их размеров. Этот эффект является чисто кинематическим, связанным с выбранным способом определения (измерения) длины и конечно­стью скорости распростране­ния взаимодействий. Его можно пояснить и так, что понятие длины перестало в СТО быть характеристикой только одного тела, самого по себе, а стало совместной характеристикой тела и системы отсчета (подобно скорости тела, его импульсу, кинетической энергии и т. п.).

Такие характеристики, изменяются для разных тел в одной и той же ИСО, что естест­венно и привычно для нас. Но так же, хотя и менее привычно, они изменяются и для одного и того же тела, но в разных ИСО. При малых скоростях движения этот эффект зависимости длины тела от выбора ИСО практически незаметен, почему в механике Ньютона (механике медлен­ных движений) он и не обращал на себя внимания.

Подобный же анализ преобразований Лоренца на предмет выяснения соотно­шения между длительностями двух процессов, измеряемыми из разных ИСО, одна из которых является собст­венной, т. e. движется вместе с носителем процесса и измеряет его длительность (разностьмоментов конца и начала процесса) _о одними и теми же часами, приводит к следующим результатам:

^ = _о(1 - V²с²), где _о - собственная длительность процесса (отсчитываемая одними и теми же часами, движущимися вместе с происходящими событиями, а ^ - длительность того же процесса, от­считываемая разными часами в ИСО, относительно которой носитель процесса движется и в моменты начала и конца процесса он находится в разных ее местах.

Иногда этот эффект интерпретируют так: говорят, что движущиеся часы идут медленнее неподвижных, и отсюда выводят ряд парадоксов, в частности парадокс близнецов. Следует отметить, что вследствие равноправия всех ИСО в СТО, все кинематические эффекты (и сокра­щения длины в направлении движения, и замедления времени - длительности движущимися относительно носителя процес­са часами) являются обратимыми. И хороший пример такой обратимости пред­ставляет собой опыт с мю-мезонами, нестабильными частицами, образую­щимися в результате взаимодействия с атмосферой, бомбардирующих ее космических лучей. Физиков вначале удивило существование этих частиц на уровне моря, где они должны были бы распасться за время их жизни, т. е. не успеть до­лететь от верхних слоев атмосферы (где они образуются) до уровня моря.

Но дело оказалось в том, что физики вначале применили в расчетах соб­ственное время жизни -мезонов _о = 210^-6 с, а расстояние, проходимое ими брали лабораторное, то есть l = 20 км. Но либо в таком случае нужно и длину (путь, проходимый -мезонами) брать собственную, которая оказывается "сокращенной", "укороченной" соответственно множителю (l –V²/с²). Либо нужно не только длину, но и время брать лабораторным, а оно возрас­тает пропорционально 1/(l–V²/с²). Таким образом, релятивистские эффекты преобразования временных и пространственных интервалов позволили физикам увязать концы с концами в реальном эксперименте и явлении природы.

При малых скоростях V  с релятивистская формула преобразо­вания длительностей процессов переходит в классическую   ^. Соответственно длительность в этом предельном случае (приближении) теряет реля­тивистскую относительность и становится абсолютной, т. е. не зависящей от выбора ИСО.

Пересматривается в СТО и закон сложения скоростей. Его релятивистскую (общую) форму можно получить, взяв дифференциалы от выражений для х, х^, t и t^, в формулах преобра­зований Лоренца и, поделив dх на dt и dх^ на dt^, то есть, образовав из них скорости _х = dх/dt и _х^ = dх^/dt^.

dх = (dх^ + Vdt^)/(l –V²/с²); dt = (dt^ + Vdх^/с²)/(l –V²/с²); 

dх/dt = (dх^ + Vdt^)/(dt^ + Vdх^/с²) = (dх^/dt^ + V)/[1 + V(dх^/dt^)/с²]  _х = (_х^ + V)(1 + V_х^/с²)

dх^ = (dх - Vdt)/(l –V²/с²); dt^ = (dt - Vdх/с²)/(l –V²/с²); 

dх^/dt = (dх - Vdt)/(dt - Vdх/с²) = (dх/dt - V)/[1 - V(dх/dt)/с²]  _х^ = (_х - V)(1 - V_х/с²)

Формулы _х = (_х^ + V)(1 + V_х^/с²) и _х^ = (_х - V)(1 - V_х/с²) и выражают собой реля­тивистские законы сложения скоростей или, иначе говоря, преобразования скоростей при пере­ходе от ИСО (К) к ИСО (К^) и наоборот.

В дорелятивистском пределе малых скоростей   c эти формулы переходят в хорошо известные выражения классического (галилеевского) закона сложе­ния скоростей: _х = _х^ + V и _х^ = _х – V.

Интересно проследить, как релятивистская форма закона сложения скоростей согласована с принципом постоянства скорости света во всех ИСО. Если в ИСО (К^) имеем скорость _х^ = с и ИСО (К^) движется относительно ИСО (К) тоже со скоростью V = с, то и относительно ИСО (К) скорость света будет по пре­жнему равна с:

_х = (_х^ + V)(1 + V_х^/с²) = (с + с)(1 + сс/с²) = с. Классический же закон сложения приводил к результату: _х = _х^ + V = с + с = 2с, т. е. противоречил опыту, ибо не содержал в себе ограничений на "потолок" скоростей.

Интервал между событиями.

В отличие от механики Ньютона, где пространство и время - как универ­сальные опреде­ленности (отношения) тел и процессов были абсолютны и не­зависимы друг от друга, в СТО вскрывается их относительный характер, их тесная взаимосвязь и опосредованность друг другом. Это дало основание Г. Минковскому объединить пространство и время в единый 4-х мерный мир (мир Минковского) с четырьмя координатными осями: Х, , Z, сt. Каждая точка в таком пространстве-времени изображает некоторое событие, т. е. нечто, происходящее там-то и тогда-то". Расстояние между двумя точками-событи­ями в этом мире называется интерва­лом S₁₂ и выражается соотношением:

S₁₂ = [с²(t₂² – t₁²) – (х₂ – х₁)² – (y₂ – у₁)² – (z₂ – z₁)²] = (с²t₁₂² – l₁₂²), где t₁₂ = t₂ – t₁ и l₁₂ = [(х₂ – х₁)² + (y₂ – у₁)² + (z₂ – z₁)²].

Каждая из компонент интервала - временная t₁₂ и пространственная l₁₂, т. е. длительность и длина, оказываются в СТО сами по себе относительными, изменяющимися в разных ИСО, но изменяющимися взаимосогласованно, так, чтобы обеспечить неизменность (инвариант­ность), постоянство в разных ИСО всего 4-х мерного интервала. И эта инвариантность новой величины - ком­бинации из прежних инвариантных - длины и длительности, является одним из важнейших результатов СТО.

Установленная в СТО тесная взаимосвязь пространства и времени наглядно иллюстри­рует диалектико-материалистическое положение о пространстве и времени как атрибутах (неотъемлемых характеристиках) единого материального мира.

Лекция 17. Пространство-время и гравитационное поле. Искривление простанства-времени. Экспериментальная база современных представлений о пространстве-времени и гравитации.

В I915 - I916 гг. А. Эйнштейн обобщил специальную теорию относительности, сняв ее ограниче­ние рамками лишь частного случая систем отсчета, а имен­но - инерциальных систем. Фактически это ограничение предполагало пренеб­режение гравитационным полем, ибо свободное (инерциальное) движение - движение без учета взаимодействий, переносчиками которых являются поля.

В основу общей теории относительности (ОТО) Эйнштейн положил принцип эквива­лентности, согласно которому свойства и законы движения в неинерциальной системе отсчета должным быть такими же, как в ИСО, но при наличии и учете в последней гравитационного поля. Таким образом, неинерциальная система отсчета, точнее ее неинерциальность, эквивалентна некоторому гравитаци­он­ному полю, т. е. все явления, обусловленные неинерциальностью системы от­счета, фактически обусловлены действием сил тяготения в ИСО.

Эйнштейн привлек внимание к тому, что если справедлив принцип эквивалентности, то совершенно невозможно отличить падение тел под действием силы тяжести от падения под действием инерции. Таким образом, гравитация и инерция в некотором смысле приводят к одинаковым эффектам.

Принцип эквивалентности сил тяготения и инерции Эйнштейна формулируется следующим образом: ускорение системы отсчета эквивалентно возникновению сил тяготения.

Гравитационная масса тела точно равна его инерционной массе (входящие, соответственно, в законы всемирного тяготения и во II закон Ньютона). Это экспериментальный факт, обусловленный, очевидно, наличием бесконечного числа тел во Вселенной.

Согласно ОТО гравитация обусловлена искривлением четырехмерного пространства-времени вблизи массивных тел.

Эффект замедления времени. Теория относительности установила не только искривление пространства под действием полей тяготения, но и замедление хода времени в сильных гравитационных полях. Даже тяготение Солнца - достаточно небольшой звезды по космическим меркам - влияет на темп протекания времени, замедляя его вблизи себя. Поэтому если мы пошлем радиосигнал в какую-то точку, путь к которой проходит рядом с Солнцем, путешествие радиосигнала займет в таком случае больше времени, чем тогда, когда на пути этого сигнала ничего нет. Замедление вблизи Солнца составляет около 0,0002 с.

Одно из самых фантастических предсказаний общей теории относительности - полная остановка времени в очень сильном поле тяготения. Замедление времени тем больше, чем сильнее тяготение. Замедление времени проявляется в гравитационном красном смещении света: чем сильнее тяготение, тем больше увеличивается длина волны и уменьшается его частота. При определенных условиях длина волны может устремиться к бесконечности, а ее частота - к нулю.

Со светом, испускаемым Солнцем, это могло бы случится, если бы наше светило вдруг сжалось и превратилось в шар с радиусом в 3 км или меньше (действительный радиус Солнца равен 700 000 км). Из-за такого сжатия сила тяготения на поверхности, откуда и исходит свет, возрастает на столько, что красное гравитационное смещение окажется действительно бесконечным. Радиус такой поверхности называется гравитационным радиусом.

С нашим Солнцем этого никогда на самом деле не произойдет. Но другие звезды, массы которых в три и более раз превышают массу Солнца, в конце своей жизни и действительно испытывают, скорее всего, быстрое катастрофическое сжатие под действием своего собственного тяготения. Это приведет их к состоянию черной дыры. Черная дыра - это физическое тело, создающее столь сильное тяготение, что красное смещение для света, испускаемого вблизи него, способно обратиться в бесконечность.

Гравитационное замедление времени, мерой и свидетельством которого служит красное смещение, очень значительно вблизи так называемых нейтронных звезд, а вблизи черной дыры, у ее гравитационного радиуса, оно столь велико, что время там как бы замирает. Тело, наблюдаемое издалека, будет бесконечно долго приближаться к гравитационному радиусу и никогда не достигнет его. В этом проявляется замедление времени вблизи черной дыры. Таким образом, материя влияет на свойства пространства и времени.

Наличие гравитационного поля вызывает искривление, неевклидов характер четырехмерного пространства-времени. Кратчайшее расстояние между двумя ми­ровыми точками в пространстве-времени отсчитывается вдоль так называемой геодезической линии.

Согласно Эйнштейну, никаких специальных гравитационных взаимодействий и порождаемых ими сил тяготения не существует, и всякое тело движется в пространстве - времени "свободно" вдоль геодезических линий. При этом в обычном 3-хмерном пространстве тело движется в общем случае вдоль криволинейных траекторий с переменной скоростью, т. е. так, как оно двигалось бы под дейст­вием некоторой силы. Например, земля движется вокруг Солнца по искривленной траектории (эллип­тической орбите) не потому, что какие то силы искривляют ее движение, а потому, что она беспрепят­ственно скользит в искривленном массивным Солнцем пространстве - времени вдоль геодезичес­кой линии. Таким образом, по Эйнштейну, тяготение есть свойство самого пространства-времени, а не некое внешнее воздействие на его фоне.

Если в СТО пространство и время, бывшие ранее обособленными, объеди­нились в единое четы­рехмерное многообразие, то в ОТО они связались с Мате­рией, ее концентрацией и распределением в пространстве.

Лекция 18. Фундаментальные физические поля. Концепции дальнодействия и близкодействия в физике. Обменно-полевой характер физических взаимодействий. Корпускулярно-волновая двойственность свойств и проявлений физических полей.

На уровне неживой природы материя существует в двух взаимосвязанных видах или состояниях - вещественном и полевом. Поле, в отличие от вещес­тва, является пространственно - делокализованным, т. е., как бы пространст­венно размазанным, непрерывно распределеннымв пространстве, не обладаю­щим определенной формой, размерами, местоположением.

Силы, которые зависят только от координат⁷, могут быть заданы с помощью поля сил - области пространства, в каждой точке которого на тело действует определенная сила. Примерами силовых полей являются гравитационное поле и, в частности, поле силы тяжести, электростатическое поле и др.

Силы (и поля), работа А₁₂ которых на пути между двумя любыми точками 1 и 2 не зависит от формы траектории между ними, называются потенциальными, а если они стационарны, их называют консервативными. Потенциальными являются все однородные поля (в каждой точ­ке таких полей сила неизменна), а также поля центральных сил (они зависят только от расстояния между взаимодействующими точками и направлены вдоль прямой, их соединяющей).

Получим формулу взаимосвязи силы таких полей с потенциальной энергией, отталкиваясь от взаимосвязи работы с потенциальной энергией А₁₂ =  = Е_п1 - Е_п2 , или, для элементарной работы: А = = - dЕ­_п. Имея в виду, что = F_sds, где ds =   - элементарный путь (и модуль перемеще­ния), а F_r = Fcos  - проекция вектора на перемещение , запишем:

F_rdr = - dЕ­_п, где -dЕ­_п есть убыль потенциальной энергии на перемещении dr. Отсюда F_r = - Е_пr; частная производная r берется по некоторому заданному направлению .

В векторной форме полученную дифференциальную взаимосвязь силы с потен­циальной энергией можно записать в следующем виде:

= -( Е_пх + Е_пу + Е_пz) = - grad Е_п = - Е_п, где символический векторный оператор  (векторная сумма первых частных производных по пространственным координатам) называется оператором Набла или градиентом скалярной функции (в данном случае - потенциальной энергии).

И

так, сила = - grad Е_п = - Е_п в потенциальном поле есть антиградиент (градиент со знаком минус) потенциальной энергии, или, иначе – пространственная производная, то есть быстрота убыли потенциальной энер­гии в пространстве в некотором направлении.

Смысл градиента можно прояснить, введя понятие эквипотенциальной поверхности, во всех точках которой потенциальная энергия Е_п имеет одно и то же значение, т. е. Е_п = const.

Из формулы = - Е_п следует, что проекция вектора на направ­ление касательной к эквипотенци­альной поверхности в любой ее точке равна нулю. Это значит, что вектор нормален к эквипотенциальной поверхности E_п = const.

Если, далее, взять перемещение dr в сторону убыли Е_п, то dЕ_п < 0 и F_r > 0, т. е. вектор направлен в сторону убыли Е_п. Градиент же от Е_п есть вектор, на­правленный по нормали к эквипотенциальной поверхности в сторону наибыстрейшего возрастания скалярной функции (здесь - потенциальной энергии). Сила же направлена в сторону наибыстрейшей убыли потенциальной энергии.

На примере гравитационного поля, сила которого прямо пропорциональна массе тела, т. е. F = m₁m₂r², можно считать, что каждое из взаимодействующих тел находится в силовом поле другого: F = mМr² = gm , где g = Fm = Мr² - напряженность гравитационного поля (удельная сила - в расчете на единицу массы), создаваемого телом массой М.

Из связи силы с потенциальной энергией следует:

dА = = m = - dЕ_п  = - dЕ_пm = - d

или  = ₁ - ₂ , где  = Е_п/m - потенциал гравитационного поля, представляющий собой удельную (на единицу массы) потенциальную энергию.

Или = - grad  = -  - формула взаимосвязи напряженности и потенциала гравитационного поля; напряженность есть антиградиент потенциала.

Вещество способно порождать и поглощать поле, которое, в свою очередь, в современной физической концепции близкодействия выступает в роли переносчика взаимодействия, осуществ­ляющего перенос и обмен движением между взаимодейст­вующими телами.

В физике взаимодействия его переносчик - физическое поле подразделяется на четыре фун­даментальных вида (состояния): гравитационное, электромагнитное, сильное и слабое. Наиболее освоенным в человеческой практике, в современной технике (особенно электро- и радиотехнике, электронике) является электромагнитное взаимодействие и его переносчик - электромагнитное поле. Оно является, например, причиной таких сил, как силы упругости и натяжения, силы трения и сопротивления.

В электромагнитном взаимодействии участвуют тела, обладающие электрическим зарядом и/или магнитным моментом. Такие тела создают в окружающем пространстве электромагнитное поле, которое проявляет себя в силовом действии (т. е. в изменении состояний движения) на другие тела, обладающие электрическим зарядом и/или магнитным моментом.

Электрический заряд (и магнитный момент) являются характеристикой тел, определяющей меру интенсивности участия их в электромагнитном взаимодействии.

Электромагнитное взаимодействие и поле являются универсальными, т. к. все три элементар­ные частицы атомов вещества (электрон, протон и нейтрон) обладают магнитным моментом, а элек­трон и протон - и электрическим зарядом.

В зависимости от состояния движения (скорости ) электрически тел, создавае­мое ими электромагнитное поле может существовать в следующих конкретных видах (состояниях):

1) статическом (электростатическом) - при  = 0;

2) стационарном (электрическом и магнитном) - при  = соnst  0;

3) нестационарном (едином электромагнитном) - при  = var (  const).

В статическом и стационарном состояниях электромагнитное поле расщепляется на обособ­ленные электростатическое и магнитостатическое поля. В нестационарном состоянии электрическое и магнитное поля взаимоувязываются в единое электромагнитное поле, которое может существо­вать либо в связанном, с породившими его источниками состоянии, например, в виде электромаг­нитных колебаний, либо в свободном состоянии, в виде распространяющихся в пространстве со скоростью света электромагнитных волн.

В классической (неквантовой) теории электромагнитного поля - электродинамике Максвелла (1864 г) наиболее общие уравнения электромагнитного поля - уравнения Максвелла, описывают нестацио­нарное электромагнитное поле и содержат в себе как частный случай уравнения для ста­ционар­ных электрического и магнитного полей и для электростатического поля.

В истории оптики известны две конкурирующие концепции – волновая и корпускулярная, которые представляли свет либо в виде непрерывных волн, либо в виде частиц (корпускул⁸). В XIX веке, в связи с разработкой Максвеллом классической электродинамики и обнаружением электромагнитной природы света, казалось, что победу одержала волновая концепция. Она наглядно объясняла такие известные оптические эффекты, как интерференция, дифракция, поляризация, поглощение света. Но к началу XX века выявились ограниченные возможности волновой концепции света в объяснении ряда других опытных оптических закономерностей и, в первую очередь, теплового излучения и фотоэффекта.

При анализе теплового излучения М. Планк в 1900 г. выдвинул гипотезу, сближавшую волновую и корпускулярную концепцию света. Суть ее в том, что свет, будучи электромагнитной волной, излучается элементарными, неделимыми далее порциями (квантами), энергия Е которых определяется только частотой  света:

Е = h, где h  6,610^-34 Джс - постоянная Планка⁹.

Эти элементарные энергетические порции света (электромагнитной волны) были впоследствии названы фотонами (фотос – с греческого – свет), частицами света. Интенсивность света при этом определяется числом фотонов, содержащихся в световой волне с данной частотой.

По формуле Эйнштейна Е = (m²с⁴ + с²р²), связывающей энергию Е с импульсом р, - для фотона, как безмассовой частицы с m = 0, получаем: Е = ср – закон дисперсии. Отсюда импульс фотона р = Е/c = h/с = h/. Формулы Е = h и р = h/ выражают взаимосвязь корпускулярных характеристик – энергии Е и импульса р с волновыми характеристиками – частотой  и длиной волны  применительно к фотону. Такое непривычное для макрообъектов сочетание волновых и корпускулярных характеристик и свойств в одном объекте получило название корпускулярно-волнового дуализма (дуализм – двойственность по французски).

В итоге, про свет можно сказать, что он имеет электромагнитную природу и двойственные – волновые и корпускулярные свойства. Сам же свет можно определить как энергетически квантованные электромагнитные волны определенного диапазона частот (длин волн).

Идея корпускулярно-волнового дуализма означает сочетание, сосуществования в элементарном объекте одновременно и волновых, и корпускулярных (“частичечных”) свойств.

Фотоны, будучи элементарными световыми (электромагнитными) волнами, являются, в отличие от частиц, делокализованными¹⁰, то есть непрерывно распределенными в пространстве, но ведут себя как элементарное, неделимое целое образование.

Фотоны долгое время не признавали частицами, т. к. они обладают волновыми свойствами (могут взаимно компенсировать друг друга), делокализованы, и легко рождаются и уничтожаются. Однако в XX веке выяснилось, что все эти особенности присущи и другим, вещественным частицам. Поэтому в настоящее время общепризнанным является понимание фотонов, как фундаментальных частиц, являющихся квантами свободного (распространяющегося) электромагнитного поля, переносящими электромагнитное взаимодействие.

Лекция 19. Биологическое поле, как совокупность физических полей (элетромагнитного, температурного и др.), связанных с живым организмом. Опыты Гуляева и Годика.

Вокруг любого биологического объекта в процессе его жизнедеятельности возникает сложная картина физических полей. Их распределение в пространстве и изменение во времени несут важную биологическую информацию, которую можно использовать, в частности, в целях медицинской диагностики.Прежде всего сформулируем, о каких полях идет речь.

Естественно, что биологический объект, как любое физическое тело, должен быть источником равновесного электромагнитного излучения. Для тела с температурой около 300 К такое тепловое излучение наиболее интенсивно в инфракрасном диапазоне волн. В этом диапазоне биологический объект, например человек, излучает очень большую мощность - свыше 10 мВт с квадратного сантиметра поверхности своего тела, т.е. в целом более 100 Вт. Это излучение далеко уходит от человека, попадая в «окно» прозрачности атмосферы (длина волны 8-14 мкм).

Следует подчеркнуть, что нас интересуют не сами по себе электромагнитные излучения биологических объектов, а возможность переноса по этим каналам информации, связанной с работой внутренних органов. Например, инфракрасное излучение промодулировано физиологическими процессами. которые задают распределение и динамику температуры поверхности тела.

Следующий канал (диапазон волн) - радиотепловое излучение, несущее информацию о температуре и временных ритмах внутренних органов человека. Так, в дециметровом диапазоне волн удается регистрировать сигналы с глубины до 5-10 см. На более коротких волнах глубина, с которой получается информация, уменьшается, однако улучшается пространственное разрешение. По радиотепловым изображениям на различных длинах волн с помощью достаточно сложной цифровой обработки можно восстановить пространственное распределение температуры в глубине биообъекта.

Низкочастотные электрические поля (с частотами до 1 кГц) связаны, как правило, с электрохимическими (в первую очередь транcмембранными потенциалами, отражающими функционирование различных органов и систем биообъекта (сердца, желудка и др.). К сожалению, низкочастотные электрические поля практически полностью планируются высокопроводящими тканями биообъекта. Это затрудняет решение обратных задач по определению источников таких полей на основе измерений электрического потенциала вблизи поверхности тела.

На тех же частотах должны наблюдаться и магнитные поля, связанные с токами в проводящих тканях, сопровождающими физиологические процессы. Для магнитных полей (в отличие от электрических) ткани биологического объекта не являются экраном, поэтому, регистрируя магнитные поля, можно с большей точностью локализовать их источники. Это, в частности, представляет большой интерес для исследования деятельности мозга. Сейчас работы такого рода, сулящие большие перспективы для медицинской диагностики, стали широко развиваться и мировой пауке.

Если говорить о более высоких частотах, то в оптическом, ближнем инфракрасном и ближнем ультрафиолетовом диапазонах должны наблюдаться сигналы биолюминесценции, обусловленной протекающими и организме биохимическими реакции. Это слабое свечение тоже весьма информативно: оно позволяет контролировать темп биохимических процессов.

о нескольких мегагерц. В связи с этим исключительно интересно изучение собственных акустических сигналов, выходящих из глубины организма. Такие исследования включают прослушивание организма в инфразвуковом диапазоне, дающее важную информацию о механическом функционировании внутренних органов, мышц и т.д. Высокочастотные акустические сигналы (в том числе шумового характера) могут быть связаны с возможными источниками на клеточном и молекулярном уровнях. Принципиально важна возможность локализации источников акустического излучения с достаточно высоким пространственным разрешением, так как длина акустической волны намного меньше, чем электромагнитной той же частоты.

Наконец, помимо названных каналов, важны измерения состава и физико-химических характеристик среды, окружающей биологический объект. В процессе метаболизма биологический объект вносит в нее возмущения - изменяет газовый и аэрозольный состав, концентрацию ионов. При этом изменяются проводимость и диэлектрическая проницаемость, коэффициент преломления среды.

Изучение физических полей биообъектов методологически очень близко к пассивному дистанционному зондированию Земли, атмосферы и т.д. В применении таких методов накоплен большой опыт. Нет необходимости объяснять, сколь важную информацию о структуре и функционировании объекта они дают.

С точки зрения дистанционного зондирования биологические объекты имеют ряд принципиальных отличий от обычных физических объектов. Состояние биообъекта существенно нестационарно. По этой причине картину его физических полей можно изучать лишь путем привязки к быстро меняющемуся психофизиологическому состоянию организма, для чего одновременно с физическими измерениями физиологи должны регистрировать различные физиологические параметры биообъекта. Кроме того, любой биообъект - динамическая саморегулирующая система, поэтому в картине его физических полей должны существенно проявляться характеристики регуляторных систем гомеостаза, исследование которых также невозможно без тесного сотрудничества с физиологами.

Эти отличия выдвигают специфические требования к аппаратуре. Из-за нестационарности биообъектов необходимо регистрировать сигналы по многим каналам одновременно, включая электрофизиологический контроль. Для получении пространственной структуры поля в каждом канале необходимо использовать матричный или сканирующие антенны. Аппаратура должна быть достаточно быстродействующей, чтобы успевать регистрировать сигналы в динамике, т.е. быстрее, чем изменяется состояние объекта. Практически во всех каналах необходимо тщательное экранирование от помех.

Наша задача состоит не в разработке принципиально новой аппаратуры, а в применении современной техники дистанционного зондирования в целях исследования биологических объектов и, главное, в создании методики таких исследований. Как правило, технику приходится модернизировать с учетом особенностей биологического объекта, разрабатывать отдельные элементы и узлы. При этом используется богатый опыт, накопленный при разработке разнообразных датчиков физических полей (полупроводниковых, сверхпроводниковых, фотоэмиссионных и др.), а также аппаратуры для пассивного зондирования.

К настоящему времени создана аппаратура для исследования электрических полей биологического объекта. В 13 электрически экранированной комнате (клетке Фарадея) дистанционно регистрируется электрокардиограмма. Для этого достаточно поднести руку к антенне - потенциальному зонду - на расстояние до 10 см.

Дистанционно (на расстояниях до 2 м) регистрируются так называемые баллистограммы. Работа внутренних органов (например, легких, сердца и др.) вызывает сотрясения поверхности грудной клетки, отражающие механические ритмы, свойственные этим органам. А поскольку на поверхности тела всегда есть статический заряд, то он, двигаясь вместе с грудной клеткой, приводит к появлению на потенциальном зонде значительных электрических сигналов.

Наша аппаратура дистанционно регистрирует и более тонкие сигналы - микротремор мышц (миограмму), вариации поля поверхностного заряда, связанные с изменениями электрических параметров кожи. Совместно с медиками начаты исследования возможностей использования этих сигналов для дистанционной медицинской диагностики.

На основе тепловизорной системы и специализированного микропроцессора для обработки изображений создан комплекс аппаратуры, регистрирующий инфракрасное излучение в диапазонах 3-5 и 8-14 мкм. Комплекс позволяет получать термограммы биообъекта с высокой чувствительностью (0,05 К).

Следует отметить, что в медицине тепловидение пока используется односторонне. Термограммы, как правило, сравнивают с некими установленными ранее нормалями и по наличию отклонений фиксируют патологию.

Мы подошли к делу иначе. Поскольку биологический объект, как уже говорилось, это прежде всего саморегулирующаяся система, изображение, получаемое по любому каналу, должно содержать информацию о регуляторных системах. Температура биологического объекта - это параметр, регулируемый системами гомеостаза. Поэтому была поставлена цель увидеть в пространственной структуре термограммы и ее временной динамике проявления этих систем и определить их характеристики. Мы ожидали, что после внешнего воздействия (нагрева или охлаждения участка тела) температура будет возвращаться к исходному значению с характерным для работы следящей системы перерегулированием. Разработаны программы цифровой обработки термограмм, позволяющие построить графики релаксации температуры для любой из 128х128 точек, описывающих термограмму, а также очертить области с одинаковой динамикой.

И действительно, удалось установить, что в термограмме человека наряду с областями, где температура релаксирует монотонно, есть также области, охваченные активным регулированием.

Такой подход позволяет уже на данном этапе oxарактеризовать точки или области точек, ведущие себя однотипно, некими функциональными параметрами, т.е. характерной постоянной времени, сигналом рассогласования.

Это важно для ранней диагностики, потому что она связана с контролем состояния регуляторных систем гомеостаза, в которых прежде всего должны появляться изменения, приводящие впоследствие к патологии.

По инфракрасному каналу в настоящее время дистанционно регистрируется целый ряд сигналов: колебания температуры кистей рук (с периодом приблизительно 2 мин), вариации температуры лица в ритме дыхания и др.