МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Московская государственная академия ветеринарной медицины и биотехнологии имени К.И.Скрябина»

________________________________________________________________________________________________

Факультет ветеринарно биологический

Кафедра информационных технологий, математики и физики

Лекции По дисциплине «Электродинамика и основы физической теории поля»

на 2012-2013 учебный год

По направлению подготовки 020400 «Биология».

Квалификация (степень) выпускника Бакалавр

Форма обучения очная

Для студентов 2 курса ветеринарно-биологического факультета

Курс лекций читают: к.ф-м.н., доц. Ю.Ф. Янченко и к.ф-м.н., доц. А.А. Олешкевич

Москва 2012

Лекция 1. Цели и задачи дисциплины. Физические поля. Электромагнитное поле и организм.

Дисциплина «Электродинамика и основы физической теории поля» является вариативной дисциплиной при подготовке бакалавров по направлению 020400 «Биология». Целью ее является овладение основами теоретической физики, необходимыми для изучения физических явлений в биологических объектах и приобретения опыта для подготовки выпускников к работе в сфере научно-исследовательской профессиональной деятельности.

Вопрос о существовании физических полей разной природы в живых организмах представляет интерес не только с точки зрения раскрытия сущности физики живого, но и в связи с взаимодействием их с полями окружающей среды и влиянием гелио- и геофизических факторов на жизнедеятельность организма. Как мы уже теперь представляем, организм - это динамическая самоуправляемая целостная система, гомеостаз (стабильность) которой обеспечен одновременным и когерентным (согласованным) функционированием как отдельных органов, так и распределенных физиологических систем - обращения крови, метаболизма, нейрорегуляции и др.

Живые объекты буквально погружены в незримый океан различных физических полей, как внешних, так и вырабатываемых самим организмом. Можно в шутку сказать, что мы находимся в «электромагнитном бульоне», и непрерывное и нормальное функционирование систем живого организма отражается в сложной картине физических полей и излучений, исходящих из него, а также в параметрических изменениях естественных фоновых полей и излучений, которые обычно окружают человека. Поэтому по картине физических полей можно судить о работе физиологических систем организма. Любой биологический объект в процессе своей жизнедеятельности генерирует излучения различной природы, которые, взаимодействуя с физическими полями внешней среды, обеспечивают живому организму необходимый ему обмен информацией. Визуализация полей и излучений из организма (сейчас в медицине уже используются рентгеновские, ультразвуковые и томографические методы, электрокардиография, электроэнцефалография и др.) позволяет «увидеть» динамику различных физиологических процессов и выявить нарушения в их работе.

Физиологическая информация заключена в пространственно-временном распределении сигналов, в их динамических изображениях. Поэтому можно образно сказать, что физические поля в организме - это «рабочий стук» физиологических процессов. Любой функционирующий орган посылает информацию по многим каналам, одни отражают быстрые процессы (биоэлектрическая активность нейтронов, мышц), другие - медленные (микроциркуляция крови, обмен веществ и т.д.). Исследование и измерение характеристик этих «стуков» - сигналов для диагностики состояния организма - может дать большой объем информации.

Если поставить вопрос более широко, то это, по существу, применение физических методов исследования биополя. В общем смысле под биополем понимается совокупность физических полей, присущих объектам живой и неживой природы, с помощью которых осуществляются их взаимодействие и обмен энергией и информацией. Точные измерения и динамическое пространственно-временное картирование этих полей, излучений и изменений фона дают возможность развития и применения новых методов ранней неинвазионной диагностики как основы профилактической медицины, в том числе разработки соответствующей аппаратуры. Этими вопросами интенсивно занимаются многие ученые у нас в стране и за рубежом, однако наибольшие успехи были получены в ИРЭ РАН под руководством академика Ю.В. Гуляева. Разработанные там методы исследования и аппаратура позволяют выделить восемь видов полей и излучений (рис.).

Одними из основных и определяющих являются электромагнитные поля (ЭМП) и излучения (ЭМИ) живого организма. Это связано с возникновением, движением и взаимодействием электрических зарядов в живом организме в процессе его жизнедеятельности. Электрические поля существующих электрических зарядов возникают при работе сердца и токе крови в сосудах, при нервных и мышечных сокращениях, генерируются при работе митохондрий в клетках и т.д. и тем самым отражают физиологическую активность различных биологических систем. В соответствии с теорией Максвелла для определения электромагнитных полей биологических объектов необходимо знать обобщенную диэлектрическую проницаемость и проводимость в биологических тканях и жидкостях.

Собственное ЭМП живого организма влияет на окружающую среду и может изменить энергию и направление движения свободных электронов, попадающих в область действия этого поля. Электрические явления характеризуются определенными последовательностями электрических импульсов и характерными ритмами. В каждом органе возникают свои специфические электрические колебательные процессы. В мозгу, находящемся в состоянии активности, регулярно проявляются a- волны, носящие ритмический характер, с частотой 9-10 Гц и потенциалом около 45 мкВ. Характер этих волн меняется в зависимости от бодрствования или сна.

Биоритмы проявляются на всех уровнях организации живой материи, от внутриклеточного до биосферы в целом. Так, у растений наблюдается суточное движение листьев, годовой ритм растительности. У животных - периодичность двигательной активности, колебания температуры, секреции гормонов, синтеза РНК и т.д. Практически все виды деятельности организма - прием пищи и питья, дыхания и другие физиологические процессы - носят циклический автоколебательный характер.

Биологические ритмы физиологической функции настолько точны, что их часто называют «биологическими часами»,. Основной механизм этих часов в клетке - биохимические колебательные процессы. Можно отметить высокую степень временной упорядоченности процессов в живом организме и возможность синхронизации их под действием слабых внешних сигналов. В последнее время выяснилось, что существенное влияние на человеческий организм оказывают слабые поля, резонансные к ряду ритмов организмов, в частности на частотах 7 и 12 Гц. В целом гомеостаз живого организма обеспечивается когерентным взаимодействием всех колебательных процессов в нем и возможностью определенного резонанса биоритмов.

На мембранах клеток может возникать разность потенциалов (50-90 мВ для нервных и мышечных клеток) за счет разности концентраций ионов во внутриклеточной и тканевой жидкости. При толщине клеточной мембраны ~ 10 нм напряженность возникающего на ней поля составляет ~ В/см, что всего лишь в 100 раз меньше напряженности, например, в атоме водорода и межатомных полей в полупроводниковом кристалле (~ В/см). Такие поля в последнем случае приводят к изгибу энергетических зон полупроводника и существенно влияют на энергетику кристалла. Плотность электрической энергии в живой клетке ~

Поэтому величина мембранного потенциала сильно влияет на весь ход физико-химических процессов в мембране, а значит и в клетке. Можно также сказать, что энергия, запасенная в виде электромагнитного поля в мембранах как своего рода конденсаторах, играет большую роль в поддержании того устойчивого неустойчивого равновесия. Ее можно рассматривать как резерв той свободной энергии, которая необходима живому организму для функционирования и развития, наряду с энергией АТФ и перекисного окисления липидов. Процессы нервного и мышечного возбуждения связаны с изменениями потенциала и протеканием биотоков.

Следует также отметить, что биоток обусловлен не только движением электронов, но главным образом ионов, участвующих в биохимических реакциях живого организма. В связи с этим возрастает роль поляризации клеток и биополимерных молекул, а также структуры воды в метаболических процессах, причем избирательная проницаемость воды будет зависеть от состояния жидкости в различных системах биологического объекта.

Кроме того, важны реологические свойства крови. Изменение электрических свойств живых организмов связано с перераспределением зарядов в организме при движении этих зарядов, в том числе в потоке крови. Кровь представляет собой жидкость, движущуюся по кровеносным сосудам и состоящую из плазмы и форменных (клеточных) элементов. Форменные элементы (эритроциты, лейкоциты и тромбоциты) взвешены в плазме. Эритроциты содержат гемоглобин и углекислоту. Лейкоциты ответственны за иммунно-защитную функцию и уничтожение элементов чужеродных для данного живого организма веществ. Тромбоциты играют основную роль в процессе свертывания крови.

По своим физическим свойствам кровь обладает электропроводностью и магнитными моментами своих элементов. А.Л. Чижевский установил системную организацию движущейся крови и наличие в ней радиально-кольцевых структур, обусловленных электрическим взаимодействием ее элементов. Форменные элементы крови заряжены отрицательно, также заряжены и стенки кровеносных сосудов. Происходит электростатическое отталкивание, и величина зарядов сильно влияет на процессы свертывания и скорость оседания эритроцитов. Свертывание крови - это электростатическое притяжение клеток крови к поврежденному участку, потерявшему естественный отрицательный заряд. При движении крови по сосудам возникают также электродинамическое, электромагнитное и гидродинамическое взаимодействия потока заряженной жидкости со стенками сосуда.

Так же как и в общем спектре электромагнитных волн, в организме можно выделить излучения разной частоты. В спектре неравновесных излучений любого биологического объекта имеются электромагнитные излучения всех частот, в том числе и радиодиапазона (ВЧ, СВЧ, КВЧ). Так, сердце можно рассматривать как поляризационный генератор СВЧ-волн. В процессе сокращения в нем, как в пьезоэлектрике, возникают высокочастотные колебания. СВЧ-поля распространяются по кровеносным сосудам, как по диэлектрическим волноводам. Так как проводимость стенок невелика, поля могут выходить за стенки такого кровеносного волновода при сгибах сосудов или изменении их диаметра при образовании, например, холестериновых отложений.

Это «просачивание» поля наружу сосудов может приводить к возникновению электромагнитных волн во всем организме, в том числе стоячих волн. Есть предположение, что в рост человека укладывается одна длина такой волны, от сердца до пальцев - 1/2 волны, до головы - 1/4 волны. Имеются также сведения, что экстремумы в распределении электрических и магнитных полей соответствуют так называемым чакрам восточной медицины и представлениям йоги. Если учитывать, что размеры человеческого тела разные, то, как утверждают экстрасенсы, и чакры у каждого человека свои. Можно предполагать в связи с этим, что йогами неизвестно как, но была изучена структура электромагнитных полей человека.

На поверхности кожи тоже может возникать биопотенциал, который связан как с внутренними электрическим полями, так и с трибоэлектрическим зарядом, возникающим из-за трения эпидермиса кожи. Эти потенциалы также отражают физиологические процессы в организме и могут быть зафиксированы соответствующей физической аппаратурой. Например, в так называемых биологически активных точках (БАТ) наблюдается значительное усиление электрического поля. Это широко используется в методах акупунктуры и электроакупунктуры для воздействия на определенный орган или процесс в живом организме.

В точках, имеющих пониженное электрическое сопротивление и повышенную концентрацию нервных волокон и микроциркуляторных сосудов, усиливается поглощение энергии из внешней по отношению к организму среды, в частности усиливается поглощение кислорода. Образуется как бы энергетический канал от активных биологических точек до соответствующего внутреннего органа. Согласно [], энергетический канал можно представить как некую ускорительную систему из упорядоченных ионов мембран, перемещающих электроны вдоль канала с ускорением. Таким образом, инжекция электронов с острия хорошо проводящей иглы в начале канала при электроакупунктуре в найденной для каждого индивидуума своей биологической точке осуществляет окислительно-восстановительные процессы в конце его. Тем самым энергетические каналы координируют протекание окислительно-восстановительных процессов, перераспределяя потоки заряженных частиц в те органы, где проходят эти реакции, усиливающие процессы жизнедеятельности или замедляющие их. Заметим, что ускоряющиеся электроны создают дополнительное внутреннее ЭМП, которое может изменить биополе человека.

В объектах живой природы обнаружены и рецепторные точки, чувствительные не только к ЭМП, но и полям другой природы, в частности к восприятию инфразвука. Этим объясняется их способность находить добычу, предчувствовать циклоны, штормы, цунами, землетрясения, магнитные бури и ориентироваться в пространстве и времени, находить воду или дорогу к местам обитания или наличия пищи и т.д. Так, муравьи, пчелы и некоторые птицы хорошо ориентируются по Солнцу (и при этом каким-то образом учитывают перемещение его в пространстве и времени, может быть, по изменению излучений от Солнца или других физических полей). Пчелам также присуще чувство времени. Они не могут определять интервалы времени, т.е. длительность времени, но довольно точно знают, когда какой цветок раскрывается, и прилетают именно к этому времени, вероятно, улавливая изменения в состоянии физических полей в окружающей их природе.

Так же как и в неживой природе, электрическое и магнитные поля живого организма взаимосвязаны. В крови животных и человека обнаружен биогенный магнетит, который, по-видимому, позволяет живому организму чувствовать изменения магнитного поля Земли. Так, А.Л. Чижевским было показано, что текущая кровь имеет упорядоченную структуру. Она поддерживается электрическими и магнитными полями эритроцитов, причем магнитное поле возникает за счет вращения эритроцитов вокруг собственных осей. Магнитное поле, которое создается биологическим объектом, значительно слабее (в 10-100 тыс. раз) геомагнитного поля. Однако в живом организме оно меньше по сравнению с электрическим, поглощается за счет диамагнитных свойств тканей организма и дает больше непосредственной информации об активности мозга. Кроме того, на разработанных в ИРЭ суперпроводящем (чувствительный элемент которого охлажден до температуры жидкого гелия) квантовом интерферометре и градиентомере при хорошем подборе отношения сигнал/шум удалось снять магнитокардиограммы и магнитоэнцефалограммы, позволяющие получить информацию о магнитных полях сердца и мозга человека. Возникновение локальных магнитных полей может быть вызвано движением и взаимодействием электронов и ионов в структурах биологического объекта.

Другим важным излучением живого организма является тепловое. Мы уже знаем, что человеческий организм функционирует в довольно узком диапазоне температур (4-40°С) и чрезвычайно чувствителен к тепловому балансу внутри него (недаром мы так часто измеряем температуру при болезнях - это показатель состояния организма). Инфракрасное (ИК) тепловое излучение характеризует температуру организма через температуру кожи. Оно несет информацию о сети капиллярного кровотока, обеспечивающего терморегуляцию тела. Образно говоря, на поверхности человеческого тела непрерывно демонстрируются «ИК-фильмы», отражающие его функционирование и открывающие возможности раннего обнаружения функциональных (и потому еще обратимых) нарушений.

Методика использования ИК-излучения в сочетании с традиционными медицинскими исследованиями позволяет определить различные изменения в организме. Так, простой рефлекторный тест - задержка дыхания на вдохе - в норме вызывает охлаждение кистей рук, обусловленное спазмом сосудов и регистрируемое чувствительной ИК-аппаратурой. Известны ИК-термореакции сердца и печени на физическую нагрузку и прием сахара у пациентов со стенокардией и циррозом печени. Возможно использование термоэнцефалоскопии как метода ИК-визуализации функциональной динамики коры мозга. Это излучение наблюдается в диапазоне длин волн 3-14 мкм, интенсивность его ~, что для всей поверхности кожи составляет около 100 Вт. Оно поглощается в биологических тканях на глубине около 100 мкм.

В организме могут возникать и комбинированные излучения, например при взаимодействии электромагнитного излучения организма с его тепловым полем. Так, радиотепловое излучение дает информацию о динамике тепловых процессов внутренних органов и мозга. Это - слабое излучение с интенсивностью в дециметровом диапазоне около, однако в отличие от ИК-излучения глубина его поглощения в тканях порядка нескольких сантиметров и дает информацию из более глубоких частей организма. Физиологическая активность любого внутреннего органа сопровождается выделением тепла и притоком крови и отражается в увеличении яркости его радиотеплового свечения.

В диапазоне 0,15-0,20 ГГц возможна генерация акустоэлектрических волн в белково-липидных мембранах, которые могут сильно изменить биохимические процессы в клетке. Низкочастотные акустические сигналы несут информацию о колебательных процессах таких внутренних органов, как легкие и сердце (акустические фононы и ультразвук). В диапазоне частот 1 до 10 МГц обычно ткани прозрачны для акустических волн, но интенсивность таких волн мала () в полосе частот до 100 кГц. Длина волны в этом диапазоне около 1 мм, что в 10 раз меньше длины волны радиотеплового излучения.

Акустотепловое излучение в ультразвуковом (УЗ) диапазоне дает распределение температуры внутри тела с более высоким пространственным разрешением, чем радиотепловое, в связи со значительно меньшей длиной волны УЗ-излучения по сравнению с обычным ЭМИ. Радио- и акустотепловое излучение может быть использовано для исследования тепловой динамики внутренних органов.

Наблюдается также излучение в видимом диапазоне частот ЭМП, так называемая оптическая хемилюминесценция. Она дает информацию о насыщении тканей организма кислородом. Предполагается, что такого рода слабое свечение может дать представление об ауре человека. Разрешение такого излучения ~ 1000 фотонов с 1.

Перераспределение и перемещение электронов может происходить и в результате химических процессов индуцированного транспорта веществ, обменов молекулами, и других веществ через кожу, и это также несет информацию о состоянии организма и может быть зарегистрировано. Разработаны также баллистические методы регистраций ритмов сердца через соответствующую проводящую среду без непосредственного контакта с телом, как делается сейчас при съемке электрокардиограммы (ЭКГ).

У многих организмов имеются электромагнитные органы. Обычно электрические поля, возникающие вокруг тела любой рыбы, очень небольшие, но у некоторых рыб соответствующие органы могут генерировать электрические разряды большой мощности. Так, у скатов разность потенциалов может достигать 300 В, у электрических угрей - до 650 В. Насекомые используют акустические сигналы, животные - звуковые, разнообразные по частоте и мощности. Для лисицы, например, отмечено 36 разных звуковых сигналов [].

Таким образом, информацию о состоянии живого организма можно получить из пространственно-временного распределения сигналов от рассмотренных выше полей и излучений от биологических объектов, анализ которого позволяет проводить бесконтактную (неинвазивную) диагностику на ранних стадиях различных заболеваний. Особая ценность этих новых методов диагностики состоит в расширении возможностей изучения органов тела и мозга не в узком интервале частот видимого света, а в использовании частот, на которых эти органы «работают». Картирование и визуализация физических полей органов биологических объектов на их «собственных» частотах позволяет наблюдать физиологическую жизнь в процессе изменений во времени. Эти динамические методы, в отличие от статической классической томографии, которая дает морфологическую картину тела, могут быть использованы для ранней диагностики задолго до возникновения патологии.

Биологически активные и рецепторные точки являются теми пропускными пунктами, где происходит обмен информацией в нужном направлении. Наличие в живом организме реальных физических полей и возможность их измерения снимают мистичность представлений о сенсорных и экстрасенсорных способностях некоторых людей, которые в состоянии воспринимать и даже изменять локальные искажения этих физических полей. Сам механизм пока, конечно, не ясен до конца. Но ясно, что для этого необходимо создать условия для согласованного «считывания» информации и управления амплитудой, фазой и частотой излучений организма.

 

Лекция 2. Электромагнитное поле и его виды. Статическое электрическое поле. Электрические заряд и поле. Закон Кулона.

В физике взаимодействия его переносчик - физическое поле подразделяется на четыре фун­даментальных вида (состояния): гравитационное, электромагнитное, сильное и слабое. Наиболее освоенным в человеческой практике, в современной технике (особенно электро- и радиотехнике, электронике) является электромагнитное взаимодействие и его переносчик - электромагнитное поле. Оно является, например, причиной таких сил, как силы упругости и натяжения, силы трения и сопротивления.

В электромагнитном взаимодействии участвуют тела, обладающие электрическим зарядом и/или магнитным моментом. Такие тела создают в окружающем пространстве электромагнитное поле, которое проявляет себя в силовом действии (т. е. в изменении состояний движения) на другие тела, обладающие электрическим зарядом и/или магнитным моментом.

Электрический заряд (и магнитный момент) являются характеристикой тел, определяющей меру интенсивности участия их в электромагнитном взаимодействии.

Электромагнитное взаимодействие и поле являются универсальными, т. к. все три элементар­ные частицы атомов вещества (электрон, протон и нейтрон) обладают магнитным моментом, а элек­трон и протон - и электрическим зарядом.

В зависимости от состояния движения (скорости ) электрически тел, создавае­мое ими электромагнитное поле может существовать в следующих конкретных видах (состояниях):

1) статическом (электростатическом) - при  = 0;

2) стационарном (электрическом и магнитном) - при  = соnst  0;

3) нестационарном (едином электромагнитном) - при  = var (  const).

В статическом и стационарном состояниях электромагнитное поле расщепляется на обособ­ленные электростатическое и магнитостатическое поля. В нестационарном состоянии электрическое и магнитное поля взаимоувязываются в единое электромагнитное поле, которое может существо­вать либо в связанном, с породившими его источниками состоянии, например, в виде электромаг­нитных колебаний, либо в свободном состоянии, в виде распространяющихся в пространстве со скоростью света электромагнитных волн.

В классической (неквантовой) теории электромагнитного поля - электродинамике Максвелла (1864 г) наиболее общие уравнения электромагнитного поля - уравнения Максвелла, описывают нестацио­нарное электромагнитное поле и содержат в себе как частный случай уравнения для ста­ционар­ных электрического и магнитного полей и для электростатического поля.

В учебном курсе физики предпочтительным оказывается способ изуче­ния электромагнитного поля от простейших состояний - статического и стационарного - к более общему и сложному - к нестационарному состоянию.

К общим основным задачам учения об электромагнитном поле относят:

1. Описание электромагнитного поля, т. е., задание его основных характеристик (задание состояния) и уравнений движения.

2. Расчет характеристик поля для наиболее характерных (модельных) типов его источников.

3. Анализ внешних проявлений (воздействий) электромагнитного поля.

Электростатика, ее предмет и основные понятия. Электрический заряд и его свойства.

Предметом электростатики является электростатическое поле (ЭСП) - простейший вид (состояние) электромагнитного поля, порождаемый и неразрывно связанный с неподвижными (в данной системе отсчета) электрически заряженными телами, существующий в окружающем их пространстве и проявляющий себя в силовом действии на другие заряженные тела.

Понятие поля было введено в физике для объяснения с позиций концепции близкодействия (непосредственного действия) наблюдаемых в опыте фактов силового действия друг на друга пространственно разнесенных (не соприкасающихся непосредственно) заряженных тел.

Электрический заряд, выступает мерой интенсивности участия тел в электрическом взаимо­действии, обладает следующими характеристиками:

1. Двузначность. Различные заряженные тела могут, как притягиваться, так и отталкиваться при взаимодействии; для объяснения этого факта и было введено представление о наличии в природе электрического заряда двух знаков. Условились заряд элементарных частиц вещества - электрона считать отрицательным, а протона - положительным.

В обычном состоянии тела содержат равное количество протонов и электронов и в целом являются электрически нейтральными. При определенных условиях, например, при трении тел или их облучении, взаимокомпенсация зарядов разного знака может нарушаться, тела электризу­ются, т. е., приобретают ненулевой результирующий заряд того или иного знака.

2. Сохраняемость. При любых изменениях в замкнутой системе тел (не обменивающейся веществом с окружением) полный ее заряд (равный алгебраической сумме зарядов всех ее тел) остается неиз­менным (сохраняется) при любых изменениях, происходящих в системе. Этот закон сохранения электри­ческого заряда является проявлением, конкретизацией философского положения о несотво­римо­сти и неуничтожимости материи и ее атрибутов (неотъемлемых свойств, характеристик), одной из которых и является электрический заряд.

3. Дискретность. Существует наименьшая, неделимая далее порция электрического заряда, равная  1,610^-19 Кл. Таким элементарным зарядом обладает электрон (со знаком – минус) и протон - со знаком плюс. Единица заряда в СИ - кулон определяется через основную электрическую единицу - ампер - как заряд, переносимый через поперечное сечение проводника постоянным током силой в 1A за одну секунду: 1 Кл = 1 А1 с.

4. Релятивистская инвариантность, то есть независимость от скорости движения заряженного тела, или, иными словами, независимость от выбора ИСО.

Закон Кулона. Характер сил электростатического взаимодействия точечных зарядов и основные характеристики и уравнения электростатического поля.

Основной закон электростатики - закон Кулона (1785 г) устанавливает характер сил элек­тро­статического взаимодействия на элементарном уровне, т. е. на уровне точечных неподвиж­ных заряженных тел (точечных зарядов). В современной трактовке он утвер­ждает, что сила электрического взаимодействия между двумя точечными (а также сфериче­скими) неподвижными заря­дами q₁, и q₂ в однородной и изотропной диэлектрической среде прямо про­порциональна значениям этих зарядов, обратно пропорциональна квадрату расстоя­ния r между ними и диэлектрической проницаемости  среды и направлена вдоль прямой, со­единяющей заряды так, что одноименные заряды отталкиваются, а разноименные притягива­ются:

= - = kq₁q₂ /

- векторная

форма закона Кулона

 =  = F = kq₁q₂/r²

- скалярная

г

де r =   - расстояние между зарядами q₁ и q₂, а - вектор, соединяющий первый заряд со вторым.

Коэффициент пропорциональности k в СИ равен: k = 910⁹ Нм²/Кл². Его часто выражают в форме: k = 1/4_о, где _о = 8,810^-12 Кл²/Нм² - электрическая постоянная, являющаяся фундаментальной физической константой.

Согласно закону Кулона, силы электростатического взаимодействия между точечными заря­дами в однородной изотропной среде обладают следующими характерными особенностями:

1) являются центральными (радиальными), т. е. ~ и, таким образом, как следует из меха­ники, являются консервативными, т. е. их работа не зависит от формы траектории, а определяется лишь положениями начальной и конечной точек перемещения и равна нулю по замкнутой траекто­рии. Радиальный характер элементарных сил ЭСП обусловливает справедливость закона Кулона и для неточечных тел, но обладающих сферической симметрией.

2) обратно квадратичны удалению, т. е.F₁₂=F₂₁= F ~ 1/r₁₂²;

3) линейно связаны с величинами зарядов, т. е. F ~ q₁ и F ~ q_2;

4) ослабляются средой пропорционально ее диэлектрической прони­цаемости .

С позиций полевой концепции взаимодействия - концепции близкодействия, вводящей поле как посредник, передающий действие (движение) между телами, не соприкасающимися непосредст­венно, каждый из электрических зарядов создает в окружающем пространстве особый вид (состоя­ние) материи - электрическое поле, которое и оказывает силовое воздействие на другие заряды, изменяя состояние их движения.

Лекция 3. Напряженность и потенциал. Основные теоремы электростатического поля.

Так как поле - вид материи, непрерывно распределенный в пространстве, для его характери­стики вводят специальные функции координат (функции точки). А так как электростатическое поле является потенциальным (его силы – консервативны), то его можно характеризовать и силовой - напряженностью , и энергетической - потенциалом  - величинами (полевыми функциями).

Линейная связь сил электростатического взаимодействия с величинами зарядов позволяет ввести силовую характеристику ЭСП - напряженность - как удельную силу, т. е. силу, дейст­вующую со стороны поля на единичный неподвижный положительный заряд в данной точке поля:

= /q  единица напряженности [Н/Кл].

Т. к. F ~ q, то отношение /q = - не зависит от значения заряда q и характеризует поле само по себе (силу поля) в данной его точке.

Выражение для напряженности поля неподвижного точечного заряда q, получим из закона Кулона, из силы взаимодействия его с пробным зарядом q:

= /q = [(kqq/r²) /r]q = (kq/r³)  Е = k|q|/r²

Важным положением в электростатике является известный еще из механики принцип супер­позиции (или принцип наложения) сил, выражающий независимость их действия при наличии нескольких сил. B электростатике его обычно называют принципом суперпозиции электростатиче­ских полей, и он выражает характеристики результирующего ЭСП при наличии нескольких источ­ников (зарядов). Согласно этому принципу, при наличии нескольких зарядов напряженность создаваемого ими результирующего ЭСП определяется векторной суммой напряженностей полей, которые бы создавал каждый из этих зарядов в отдельности: =  .

Чтобы ввести энергетическую характеристику ЭСП – потенциал , необходимо сначала убе­диться в потенциальном характере ЭСП. Для этого нужно показать, что силы ЭСП являются консер­вативными, то есть их работа по перемещению заряда не зависит от формы траектории. Для про­стоты составим выражение для работы А₁₂ перемещения пробного заряда q в поле неподвиж­ного точечного заряда q:

А₁₂ = = = = kqq = kqq = kqq(1/r₁ - 1/r₂) = q(₁ - ₂).

Получили выражение, из которого следует, что работа А₁₂ сил ЭСП точечного заряда q по перемещению пробного заряда q не зависит от формы траектории перемещения, а определяется лишь его начальным и конечным положениями, задаваемых координатами r₁ и r₂. В качестве энергетической характеристики этого положения (точки поля) и выбирается скалярная величина, называемая потенциалом . Для точечного заряда  = kq/r.

Полученный результат о потенциальном характере ЭСП неподвижного точечного заряда можно обобщить на ЭСП, создаваемое произвольной системой неподвижных зарядов.

Энергетическая характеристика ЭСП - потенциал  может быть получена из известного в механике выражения, связывающего силу и потенциальную энергию, в соответствии с которым, сила есть антиградиент потенциальной энергии (или проекция силы на некоторое направление равна быстроте убыли потенциальной энергии W_п в данном направлении).

= - grad W_п  = - grad W_п/q  = - grad 

где за потенциал  принято отношение потенциальной энергии взаимодействия заряда с полем к величине заряда:  = W_п/q - удельная по заряду потенциальная энергия, то есть потенциальная энер­гия единичного положительного заряда в данной точке поля, измеряемая в вольтах:о

[Дж/Кл = В]. Или из F_х = - W_п/х  Е_х = - /х [В/м]

Из взаимосвязи силовой и энергетической характеристик ЭСП получа­ет иное выражение и трактовку единица напряженности. Будучи антиградиентом потенциала, выражая своей про­екцией быстроту убыли потенциала в соответствующем направлении, напряженность, наряду с исходным выражением = /q, определяющим ее как удельную силу (в расчете на единицу заряда), измеряется и в В/м. Эта единица показывает, на сколько вольт убывает потенциал на еди­нице длины в соответствующем направлении.

Двоякая интерпретация может быть дана и энергетической характеристике ЭCII - потен­циалу . С одной стороны, потенциал  = W_п/q - представляет собой удельную потенциальную энергию ЭСП в данной точке, т. е. потенциальную энергию, которую приобретает в данной точке поля положительный единичный заряд. С другой стороны, поскольку потенциальная энергия (энергия взаимодействия) определяется неоднозначно, с точностью до константы, а ее изменение (убыль) равно работе консервативных сил (какими и являются силы ЭСП), то и потенциал  может быть выражен через работу сил ЭСП по перемещению единичного положительного заряда из данной точки на бесконечность (потенциал точки, достаточно удаленной от источников поля может быть принят равным нулю):

А₁₂ = q(₁ - ₂)  ₁ - ₂ = А₁₂/q, или, при ₂  0 ₁ = А_1/q.

Из выражения ₁ - ₂ = А₁₂/q следует, что разность потенциалов двух точек поля есть величина, измеряемая работой сил ЭСП по перемещению положительного единичного заряда из одной точки в другую.

Для однородного ЭСП, напряженность в котором во всех точках одинакова, взаимосвязь между силовой и энергетической характеристиками упрощается и становится более наглядной:

Е_х = - /х = (₁ - ₂)/(х₂ - х₁)

Обратный переход от напряженности к разности потенциалов, выража­ется интегральным соотношением: из d = - Е_хdх 

 = ₂ - ₁ = или ₁ - ₂ =

Для однородного поля: ₁ - ₂ = Е_х(х₂ – х₁).

Для наглядности ЭСП изображают с помощью силовых линий - касательные, к которым сов­падают с направлением вектора в каждой точке поля, а их густота пропорциональна числен­ному значению напряженности ЭСП в данном месте, и с помощью эквипотенциальных поверхно­стей, все точки которых имеют одинаковый потенциал. Характерным для ЭСП является перпен­дикуляр­ность силовых линий эквипотенциальным поверхностям. Это следует из того, что вдоль эквипотен­циальной поверхности  = const, то есть d = 0, а значит проекция Е_ вектора на эквипотенциальную поверхность Е_ = - d/d = 0. Отсюда вектор перпендикулярен эквипо­тен­циальной поверхности.

Характерным для ЭСП является также то, что его силовые линии - разомкнуты. Они имеют начало - на положительных зарядах и конец - на отрицательных зарядах или в бесконечности. Замкнутость силовой линии означала бы неравенство нулю работы сил ЭСП по замкнутой траектории, совпадающей с силовой линией, что противоречит его потенциальному характеру.

Силовые линии направлены в сторону убыли потенциала, от большего его значения к мень­шему. Формально это следует из взаимосвязи напряженности и потенциала, в соответствии, с кото­рой напряженность есть антиградиент потенциала, а градиент, по определению, есть вектор, направ­ленный в сторону наибыстрейшего возрастания функции (в данном случае – потенциала).

В математическом плане ЭСП, являясь векторным потенциальным полем, полностью харак­теризуется двумя теоремами, которые в интегральной форме записываются для циркуляции и потока вектора поля (в данном случае - вектора ).

Циркуляция есть криволинейный интеграл от векторной функции поля по замкнутому контуру. Принимая во внимание смысл вектора = - сила, действующая на положительный единичный заряд, для циркуляции вектора получаем: = = = - работа сил ЭСП по перемещению положительного единичного заряда по замкнутой траектории (контуру L). В силу потенциального характера ЭСП работа его сил (являющихся консервативными) по замкнутому контуру нулю. Отсюда следует и теорема о циркуляции вектора : циркуляция вектора напряженности электростатического поля равна нулю: = = 0

Э

та теорема является следствием центрального (радиального) характера сил ЭСП ( = Edlcos  = E_ldl, где Е_l = Еcos  - проекция вектора на направле­ние d ). Из нее следует разомкнутый характер силовых линий ЭСП; в против­ном случае, перемещая заряд вдоль замкнутой силовой линии, совершали бы ненулевую работу, что противоречит условию потенциальности ЭСП.

В

торой важнейшей теоремой ЭСП является теорема о потоке вектора называемая теоремой Остроградского-Гаусса, иногда - просто теоремой Гаусса. Под потоком Ф вектора через некоторую поверхность понимают поверхностный интеграл от вектора через соот­ветствующую поверхность. Наглядно поток вектора через какую-либо поверхность представляет собой скалярную характеристику векторного поля, которая пропорцио­нальна числу силовых линий, пронизывающих соответствующую поверхность. Через элементарно малую поверхность dS, которой можно придать смысл вектор-пло­щадки¹ d , поток dФ_Е вектора будет равен произведению: dФ_Е = = ЕdScos  = Е_ndS, где  - угол между вектором и внешней единичной нормалью к площадке , а Е_n = Еcos  - проекция вектора на направление нормали . Полный же поток Ф_Е вектора сквозь поверх­ность S определится поверхностным интегра­лом: Ф_Е = =

В соответствии с этим соотношением напряженности можно придать смысл поверхностной плотности потока вектора (потока силовых линий), то есть величины, пропорциональной густоте силовых линий, то есть их числу, пронизываю­щих единичную площадку. Теорема о потоке вектора напряженности ЭСП - теорема Остроградского - Гаусса утвер­ждает, что поток Ф_Е вектора через любую замкнутую поверхность S не зависит от размера и формы поверхности, а определяется лишь полным электрическим зарядом q_, находящимся внутри замкнутой поверхности, будучи численно равным этому заряду, деленному на электрическую посто­янную _о:

Ф_Е = = q_/_о.

П

окажем на примере точечного заряда q справедливость теоремы Остроградского - Гаусса.

Окружим точечный заряд замкнутой поверхно­стью, для простоты в виде сферы радиуса R и вы­числим по­ток вектора от точечного заряда че­рез эту сфериче­скую поверхность. Выра­жение для напряженности Е поля точечного заряда q получим из закона Кулона, из силы взаимодейст­вия его с пробным зарядом q:

= /q = (kqq/r²)q  Е = kq/r² (k = 1/4_о)

Подставляя это выражение в формулу для потока вектора , получим:

Ф_Е = = = Е = ЕS = (kq/R²)4R² = q/_о.

Действительно, поток Ф_Е вектора сквозь сферическую поверхность S равен заряду, находящемуся внутри поверхности, деленному на _о. Такая связь характеристики ЭСП (потока вектора ) с источниками его порож­дающими (с зарядами), с одной стороны, является важным законом природы (следствием закона «обратных квадратов» в зависимости сил электрического взаимодействия точечных зарядов), а с другой – выступает методом для решения основной задачи электростатики - расчета характеристик поля по известному распределению его источников - электрических зарядов. Это наглядно видно на примере точечного заряда и случая сферической поверхности, поток вектора через которую, пропорционален ее площади и, соответственно, квадрату ее радиуса.

Обобщая теорему о потоке вектора ЭСП на произвольную систему зарядов, получим:

= q_/_о

где q_ = q _ - для дискретного распределения зарядов, создающих ЭСП (и поток Ф_Е).

 dl - для линейного,

и q_ = dS - поверхностного, - непрерывных распределений заряда по телу.

dv - объемного

и где  = dq/dl - линейная,  = dq/dS - поверхностная и  = dq/dv - объемная плотности заряда, изме­ряемые в Кл/м, Кл/м² и Кл/м³, соответственно. В случае равномерного распределения заряда произ­водные заменяются отношениями:  = q/l,  = q/S и  = q/V и представляют собой соответственно заряд единицы длины, единицы площади и единицы объема заряженного тела.

Учитывая, что в диэлектрической среде электрическое поле ослабляется в  раз, вво­дят вспомогательную силовую характеристику , называемую электрическим смещением или век­тором индукции электрического поля, связанную с основной силовой характеристикой ЭСП - векто­ром напряженности , следующим соотношением: = _о

Э

= = q_

та величина характеризует силу ЭСП в вакууме, т. е. ЭСП самого по себе, без учета среды. Она облегчает расчет характеристик ЭСП в неоднородных диэлектрических средах. Использование вектора позволяет придать более простой вид теореме Остроградского - Гаусса:

- поток вектора электрического смещения через любую замкнутую поверхность не зависит от разме­ров и формы этой поверхности, а определяется алгебраической суммой q_ свободных зарядов, находя­щихся внутри этой поверхности, и равен значению этого заряда.

ЭСП полностью характеризуется двумя теоремами: теоремой о циркуляции и теоремой о потоке вектора . Эти теоремы образуют полную систему уравнений ЭСП в интегральной форме.

В решении конкретных задач электростатики часто удобным оказывается использование энергети­ческой характеристики - потенциала  и вспомогательной силовой характеристики - вектора индук­ции ЭСП - . При этом необходимыми оказываются уравнения связи силовой и энергетической характеристик ЭСП = - grad  и основной и вспомогательной силовых характеристик ЭСП = _о

Фактически обе теоремы ЭСП эквивалентны одному закону Кулона и, по сути, являются его следствиями, - следствиями устанавливаемых этим законом основных свойств ЭСП - его потенци­альности (консервативности сил ЭСП) и закона "обратных квадратов" в зависимости сил от расстоя­ния.

Для перехода к дифференциальной форме записи теоремы о циркуляции воспользуемся известной из векторного анализа теоремой Стокса, связывающей циркуляцию вектора с поверхностным интегралом от ротора этого вектора:

= ,

где S – поверхность, ограниченная контуром L. Под ротором вектора понимают векторный дифференциальный оператор, задаваемый следующим образом:

rot = (Е_у/z - Е_z/у) + (Е_z/х - Е_х/z) + (Е_x/y - Е_y/x)

Физический смысл ротора вскрывают, устремляя поверхность S к нулю. В пределах достаточно малой поверх­ности ротор вектора можно считать постоянным и вынести за знак интеграла:

= rot  = rot S.

Тогда, согласно теореме Стокса: rot = (1S) при S  0.

Отсюда ротор вектора можно определить как поверхност­ную плотность циркуляции этого вектора.

Так как в ЭСП циркуляция вектора равна нулю, то равен нулю и ротор вектора :

rot = 0.

Это уравнение и есть дифференциальная форма теоремы о циркуляции вектора в ЭСП.

Для перехода к дифференциальной форме записи теоремы Остроградского – Гаусса воспользуемся известной из векторного анализа теоремой Гаусса, связывающей поток вектора по замкнутой поверхности с интегралом от дивер­генции этого вектора по объему, заключенному в этой поверхности:

= .

Под дивергенцией вектора понимают скалярный дифференциальный оператор (совокупность производных), задаваемый следующим образом:

div = Е_х/х + Е_у/у + Е_z/z.

Физический смысл дивергенции вскрывают, устремляя объем V к нулю. В пределах достаточно малого объема дивергенцию вектора можно считать постоянной и вынести за знак интеграла:

= div  = (1V) div . Тогда, согласно теореме Гаусса, div = (1V) при V  0.

Отсюда дивергенцию вектора можно определить как объемную плотность потока этого вектора.

Соотнося теорему Остроградского – Гаусса = q_/_о = (1_о) и теорему Гаусса = , видим, что левые их части равны друг другу. Приравнивая их правые части, получаем: div = _о.

Это уравнение и представляет собой дифференциальную форму теоремы Остроградского – Гаусса.

Лекция 4. Конденсаторы. Электроемкость. Энергия и объемная плотность энергии электрического поля.

Электроемкость проводника. Конденсаторы.

Потенциал , приобретаемый уединенным проводником при сообщении ему заряда q, прямо пропорционален заряду q и зависит от размеров и формы проводника, а также от окружающих его тел и полей (электрических). Отношение же С = q/, не зависит ни от заряда q, ни от потенциала  и характеризует способность проводника (назы­ваемую электроемкостью, или просто емкостью) поддерживать постоянным определенное отно­шение заряда на проводнике к его потенциалу или, иначе - удерживать (накапливать) определенный заряд при заданном потенциале. Численно емкость проводника равна заряду, при котором проводник приобретает единичный потенциал (или, изменяет его на единицу).

Единицей электроемкости является фарад: 1 Ф = 1 Кл/1 В.

Для сферического проводника радиусом R и зарядом q потенциал  равен:  = kq/R и емкость С_сф = q/ = q/(kq/R) = R/k = 4_оR.

Для устранения зависимости электроемкости от окружающих тел и электрических полей и накопления значительных зарядов применяют устройства в виде системы проводников, называе­мые конденсаторами. Простейший тип конденсатора состоит из двух проводников (называемых электродами или обкладками), разделенных диэлектриком. В зависимости от конфигурации элек­тродов различают плоские, сферические, цилиндрические конденсаторы. Они концентрируют все свое ЭСП в пространстве между обкладками, куда не проникает внешнее ЭСП, которое, поэтому и не оказывает на него никакого влияния.

Заряжение обкладок конденсатора зарядом  q сопровождается появлением между ними разности потенциалов , прямо поропорциональной сообщенному заряду q. Емкость конденсатора определяется как отношение заряда q одной из его разноименно заря­женных обкладок, к разности потенциалов между ними:

С = q/(₂ - ₁) = q/ или С = q/U

Она характеризует способность конденсатора поддерживать постоянным определенное отношение заряда на обкладках к разности потенциалов между ними или, иначе - удерживать (накапливать) определенный заряд на обкладках при заданной (например, единичной) разности потенциалов между ними. Численно емкость конденсатора равна заряду, сообщение которого обкладкам вызывает единичную разность потенциалов между ними (или ее единичное изменение).

Отсутствие влияния внешних тел и электрических полей на емкость конденсатора, т. е. на отношение q/ объясняется тем, что все ЭСП конденсатора (его разноименно заряженных пластин) сосредоточено внутри него, между его обкладками и заэкранировано ими. Сна­ружи поля конденса­тора нет и поэтому он "безразличен" к наличию или отсутствию внешних тел или полей.

Р

анее, при применении теоремы Остроградского-Гаусса для вычисления напряженности ЭСП двух разноименно заряженных пла­стин, уже было получено выражение для электроемкости плос­кого конденсатора: С = _оS/d

где S - площадь одной обкладки (пластины) конденсатора;

d - расстояние между обкладками конденсатора;

 - диэлектрическая проницаемость среды между обкладками.

У конденсатора с большей диэлектрической проницаемостью  диэлектрика между обклад­ками емкость С больше потому, что при неизменном заряде q на обкладках диэлектрик уменьшает в  раз напряженность ЭСП, а соответст­венно и разность потенциалов  = Еd между обкладками, так что отношение q/ = С – возрастает в  раз.

У конденсатора с большей площадью S обкладок емкость С больше потому, что при одинаковом их заряде q поверхностная плотность  = q/S, а, соответственно и напряженность Е = /_о и разность потенциалов  = Еd между обкладками меньше, то есть отношение q/ = С - больше.

С увеличением расстояния d между обкладками емкость С конденсатора уменьшается (при прочих одинаковых параметрах) потому, что при одинаковом заряде q на обкладках и, соответственно, при одинаковой плотности заряда  = q/S и напряженности Е = /_о, разность потен­циалов между обкладками  = Еd возрастает, а отношение С = q/ убывает обратно пропорцио­нально расстоянию d.

На практике в целях получения необходимой электроемкости (и рабочего напряжения) кон­денсаторы часто соединяют в батареи с последовательным и/или параллельным соединением.

П

ри параллельном соединении все конденсаторы имеют единое общее начало и общий еди­ный конец. При этом на каж­дом из конденсаторов одинакова разность потенциалов _ =  = const, а полный заряд q_ батареи равен сумме q_ зарядов на каждом из конденсато­ров. Ре­зульти­рующая емкость параллельного соеди­нения N конденсаторов равна:

С = q_/_ = q_/_ = q₁/ + q₂/ + … + q_N/ = С₁ + С₂ + ... + С_N = С_

- результирующая емкость равна сумме емко­стей, составляющих батарею кон­денсаторов.

При последовательном соединении конденсаторов (в цепочку, один за другим) одинаковым является заряд q_ = q = q_ на каждом из конденсаторов, а результирующая разность потенциалов _ равна сумме _ разностей потенциалов на каждом из конденсаторов². И результирующая емкость батареи из N последователь­ного соединенных конденсаторов будет равна:

С

_посл = q_/_ = q/_; 1/С_посл = _/q = _/q = ₁/q + ₂/q + ... + _N/q = 1/C₁ + 1/C₂ + ... + 1/C_N = 1/C_  1/C_посл = (1/С_) -

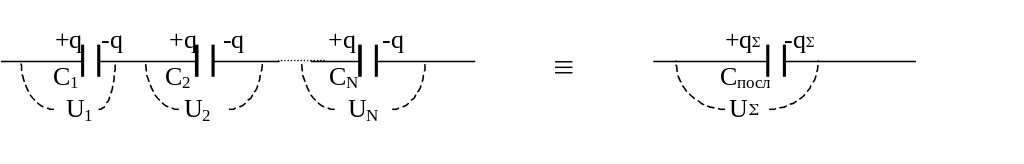
- результирующая обратная емкость 1/C_посл последовательного соединения конденсаторов равна сумме (1/С_) обратных емкостей, составляющих батарею конденсаторов (и оказывается меньше наименьшей из складываемых емкостей).

Для простейшей батареи из двух (N = 2) конденсаторов С_посл = С₁С₂/(C₁ + C₂).

Энергия заряженного конденсатора и проводника. Объемная плотность энергии ЭСП.

Электрическое поле, являясь видом материи, обладает энергией - универсальной мерой дви­жения и взаимодействия. Заряжение (электризация) проводника всегда связано с совершением работы по преодолению кулоновских сил отталкивания между одноименными зарядами, которая идет на увеличение его электрической энергии. Для переноса элементарно малого заряда dq из бесконеч­ности на проводник требуется совершить элементарную работу

А = dq = qdq/С  А^ = q²/2С = С²/2 = q/2.

Аналогично, для конденсатора работа по переносу заряда dq с одной обкладки на другую:

А = dq(₁ – ₂) = qdq/С  W_с = q²/2С = С²/2 = q/2.

Учитывая, что конденсатор - это система из двух заряженных проводников с зарядами q₁ = - q₂ = q, перепишем формулу для энергии электрического поля конденсатора:

W_с = q(₁ – ₂) = (q₁₁ + q₂₂)/2. И можно показать, что для системы из  неподвижных проводников их полная энергия

W_ =

Энер­гия конденсатора сосредоточена в пространстве между пластинами конденсатора, т. е. в объеме V = Sd.

Объемная плотность энергии ЭСП, т. е. энергия, приходящаяся на единицу объема, равна:

_э = W_э/V = q²/2CV = ²S²d/(2_оSV) = ²S²d/(2_оSSd) = ²/2_о = _оЕ²/2

Материальным носителем энергии заряженного конденсатора является не конденсатор непо­средственно и не заряды на нем, а его электрическое поле, заполняющее пространство объемом V = Sd внутри конденсатора и распределенное в нем с объемной плотностью:

_э = _оЕ²/2 [Дж/м³]

Энергия ЭСП заряженных проводников, выражаемая формулой W_э = С²/2, также распределена в пространстве с объемной плотностью

_э = _оЕ²/2

Лекция 5. Электрический ток. Сила тока и плотность тока. Законы Ома.

Электрический ток является одним из наиболее распространенных источников магнитного поля, поэтому, прежде чем переходить к изучению магнитного поля, целесообразно изучить основ­ные характеристики и законы электрического тока. Кроме того, эффекты, связанные с электриче­ским током, чрезвычайно широко используются в современной биологии.

Основные характеристики и законы постоянного тока.

При приложении к проводнику постоянной разности потенциалов в нем возникает под дейст­вием сил ЭСП уравновешивающий поток заряженных микрочастиц, который и называется электри­ческим током. Количественными характеристиками, мерами этого потока являются:

1) скалярная и интегральная по площади поперечного сечения мера быстроты переноса заряда, называе­мая силой тока:  = dq/dt или, для постоянного тока, I = q/t [1 Кл/с = 1 А]. Сила тока представляет собой поток заряда в проводнике, т. е. численно равна заряду, пере­носимому через поперечное сече­ние проводника за еди­ницу времени.

2

) векторная и локальная (дифференциальная) по площади поперечного сечения проводника мера быст­роты переноса заряда, называемая плотностью тока: j = I/S_ [1 А/1 м²] - поверхностная плотность потока заряда.

За время t через поперечное сечение проводника пройдут все носители заряда, содержащиеся в объеме цилиндра высотой t. Их число N = nV = nSt, где n – концентрация свободных носителей заряда в проводнике и  - средняя скорость их направленного движения.Они перенесут заряд q_ = qN = qnSt и создадут ток силой I = q_/t = qnS и плотность тока j = I/S = qn, где q – заряд одной свободной частицы.

Опытным путем были установлены два основных закона постоянного тока для однородного (не содержащего источников тока) участка цепи

1) Закон Ома. При приложении к однородному³ участку цепи разности потенциалов  в нем воз­никает электрический ток, сила I которого прямо пропорциональна  и обратно пропорциональна сопротивлению участка цепи: I = /R

Из этого закона выражается и получает интерпретацию одно из важнейших понятий учения об электрическом токе - понятие электросопротивления:

R = /I [1В/1А = 1 Ом].

Электросопротивление однородного участка цепи, вследствие прямо пропорциональной зависимости между силой тока I и разностью потенциалов , не зависит ни от I, ни от , а опреде­ляется лишь их отношением. С ростом разности потенциалов  на концах проводника прямо пропорционально возрастает сила тока I, протекающего через него, а отношение разности потенциалов к силе тока /I, которое и есть сопротивление проводника, остается неизменным. Сопротивление участка цепи (резистора) и есть способность его поддерживать постоянным определенное отношение между разностью потенциалов на его концах и силой тока, протекающего через него. Численно электросопротивление резистора равно разности потенциалов на нем, обусловливающей ток единичной силы в нем. Сопротивлением эта величина названа потому, что без противодействия направленному потоку заряженных частиц постоянная разность потенциалов, а, соответственно и постоянная напряженность, т. е. сила, действующая на заряженные частицы, приводили бы к непре­рывному возрастанию их скорости и, соответственно - силы тока, чего не имеет места на практике. В основе физического механизма ограничения скорости носителей заряда в металличе­ском провод­нике лежит, как показано будет ниже в классической теории электропроводности метал­лов, рассея­ние ускоряемых электрическим полем носителей заряда - электронов на разного рода несовершен­ствах состава и структуры материала (тепловых колебаниях узлов кристаллической решетки, примесях, вакансиях и т. п.).

Наряду с приведенной выше так называемой интегральной формой закона Ома, существует еще и дифференциальная (лучше сказать - локальная) форма закона Ома. Для ее получения подставим в выражение для сопро­тивления вместо интегральных характеристик - разности потенциалов и силы тока, дифференциаль­ные - напряженность и плотность тока:

R = /I = Еl/jS = l/S, где  = Е/j или j = Е/

Отношение напряженности Е в проводнике к плотности тока j в нем есть величина постоянная, зависящая лишь от свойств проводника и называемая его удельным электросопротивлением . Удель­ным сопротивлением называют сопротивление проводника единичных размеров (единичной длины и площади поперечного сечения). Это следует из выражения для электросопротивления однородного проводника:

R = l/S   = RS/l [Омм/² = Омм]   = R при l = 1 м и S = 1м².

Сопротивление однородного проводника R = l/S прямо пропорционально его длине, обратно пропорционально площади поперечного сечения и зависит от рода материала, соответствующей характеристикой которого является его удельное электросопротивление .

У более длинного про­водника при одинаковой разности потенциалов на концах меньше напряженность ЭСП Е = /l, а значит и сила F = qЕ, действующая на носители тока в проводнике. Меньшая сила сооб­щает им меньшее ускорение и, соответственно, меньшую среднюю скорость, а, значит, за единицу времени в длинном проводнике пройдет меньший заряд, т. е. ток  меньшей силы. Итак, в длинном проводнике, при той же разности потенциалов на концах, отношение R = /I, которое и выражает собой электросопротивление проводника (участка цепи), больше чем в коротком.

У более толстого проводника (проводника с большей площадью поперечного сечения) при одинаковой с тонким проводником разности потенциалов одинаковой будет напряженность ЭСП внутри проводника и сила, действующая на носители тока. Последние, будут двигаться с одина­ковым ускорением и одинаковой средней скоростью в обоих проводниках, т. е. обеспечат одина­ковую плотность тока - заряд, переносимый за единицу времени через единицу площади попе­речного сечения. Сила же тока I = jS в толстом проводнике больше чем в тонком и, значит отношение R = /I, т. е. сопротивление, у толстого проводника меньше, чем у тонкого проводника.

Физический механизм влияния  на сопротивление проводника заключается в рассеянии носителей тока на разного рода несовершенствах состава и структуры материала, которое ограничи­вает возрастание скорости носителей тока и определяет тем самым среднюю их скорость, а вместе с ней и силу тока (при фиксированной разности потенциалов).

В электро- и радиотехнике часто приходится иметь дело с последовательным, или парал­лельным соединением участков цепи, обладающих сопротивлением; их часто называют резисто­рами. Получим формулы для расчета результирующего электросопротивления соединения N резисторов:

а

) при последовательном соединении

(в цепочку, один за другим) через все

резисторы протекает один и тот же ток I, а результирующая разность потенциалов _ равна сумме _ на каждом из них:

R_посл = _/I = (₁ + ₂ + ...+ _N)/I = ₁/I + ₂/I + ...+ _N/I = R₁ + R₂ + R_N = R_

- результи­рующее сопротивление равно сумме сопротивлений последовательно соединенных резисторов.

б

) при параллельном соединении N резисторов одинаковой является разность потенциалов (₁ - ₂) на каждом из них, а результирующий ток I_ равен сумме I_ токов, протекающих через каждый из резисторов.

R_пар = (₁ - ₂)/I_ = (₁ - ₂)/(I₁ + I₂ + … + I_N) = 1/(1/R₁ + 1/R₂ + 1/R_N)  1/R_пар = 1/R_ - при параллельном соединении резисто­ров суммируются их обратные сопротивления (у конденсаторов было наоборот).

Для R₁ = R₂ = … = R_ , R_пар = R₁. Для  = 2, R_пар = R₁R₂(R₁ + R₂).

Сторонние силы. Электродвижущая сила. Закон Ома для неоднородного участка цепи и для замк­нутой цепи. ЭДС, напряжение и разность потенциалов.

Для поддержания непрерывного протекания тока в проводнике необходима замкнутая цепь и наличие в ней источника тока, в котором бы за счет работы сил неэлектростатической природы (механических, электромагнитных и др.), называемых сторонними, происходил перенос положи­тельного заряда в направлении возрастания потенциала, и поддерживалась бы постоянная разность потенциалов на полюсах источника тока.

Электростатические силы являются консервативными; их работа по замкнутому контуру все­гда равна нулю, и они переносят заряд (положительный) только в направлении убыли потенциала, стремясь соединить разноименные заряды и уничтожить имеющуюся разность потенциалов.

В

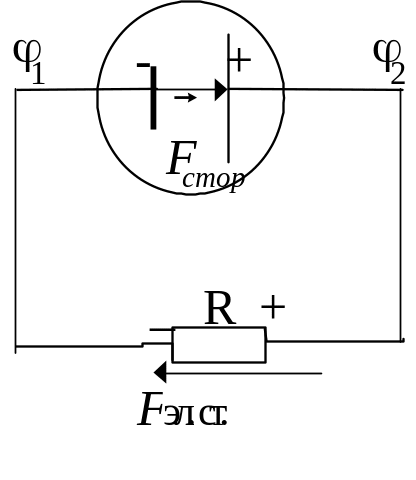
замкнутой электрической цепи на внешнем (по отношению к источнику тока) участке рабо­тают электростатические силы, направленные (вектор ) в сторону понижения потенциала. Их энергетической характеристикой служит разность потен­циалов ₁ - ₂, равная их работе А₁₂, отнесенной к величине перенесенного заряда q: ₁ - ₂ = = А₁₂/q

3а энергетическую характеристику сторонних сил принимают величину , называемую элек­тродвижущей силой и равную отношению работы А^ сторонних сил по перемещению заряда q внутри источника тока к величине этого заряда, т. е.

 = А^ /q [Дж/Кл = В]

На неоднородном участке цепи (содержащем источник тока) в общем случае могут работать и сторонние, и электростатические силы, общая работа которых по перемещению через участок заряда q равна:

А_ = А₁₂ + А^ =  _эл.ст.d +  _сторd =  q _эл.ст.d +  q _сторd = q[(₁ - ₂) + ₁₂]

Работа по перемещению единичного положительного заряда через неоднородный участок цепи называется напряжением U на данном участке цепи. Оно равно алгебраической сумме ЭДС и разности потенциалов на данном участке цепи:

U = А_/q = (₁ - ₂) + ₁₂

Е

сли для однородного участка цепи (где отсутствует источник тока, и работают только элек­тростатические силы) закон Ома имел вид:

I = (₁ - ₂)/R₁₂, то для неоднородного участка его есте­ственным обобщением будет:

I = [(₁ - ₂) + ₁₂]/R₁₂ = U/R_{12 ,}

где R₁₂ = R + r и r - внутреннее сопротивление источника тока. Оно равно отношению ЭДС  к току короткого замыкания (току, при внешнем сопротивлении R = 0).

Е

сли участок цепи, содержащий источник тока замкнут на внешнее сопротивление (сопро­тивление нагрузки), т. е. ₁ = ₂ и ₁ - ₂ = 0, то закон Ома для него примет следующий вид:

I = ₁₂/R₁₂ = /(R + r) - закон Ома для замкнутой цепи.

Лекция 6. Электронная теория электропроводности. Закон Ома и Джоуля-Ленца в дифференциальной форме.

Закон Джоуля – Ленца. При приложении к однородному участку цепи с сопротивлением R разности потенциалов , в нем протекает элек­трический ток силой I, и за время t на участке цепи выделяется теплота Q, пропорциональная силе тока, разности потенциалов и времени прохождения тока: Q = It.

Тепловая мощность электрического тока, выделяющаяся на участке цепи (на его сопротивлении):

Р = Q/t = I = I²R = ()²/R [Дж/с = Вт]

Формально закон Джоуля - Ленца может быть получен как следствие закона Ома:

при пере­носе заряда q за время t по участку цепи с разностью потенциалов  = IR совершается работа рав­ная: А = q = I²Rt, которая и идет на нагрев участка цепи, т. е. выделяется в виде тепла (если уча­сток цепи неподвижен, и в нем отсутствуют химические превращения).

Наряду о приведенной выше интегральной формой закон Джоуля - Ленца имеет, как и закон Ома и дифференциальную форму, справедливую локально, т. е. в точке (в физически бесконечно малом объеме): ее можно получить из интегральной формы, заменяя в ней интегральные харак­теристики - , I, и R на соответствующие дифференциальные – Е, j , и :

Р = I = Е l(j S) = jЕSl = jЕV  Р_уд = Р/V = jЕ = Е²/

Общность законов Ома и Джоуля - Ленца имеет не только формальные, но и глубокие содер­жательные, сущностные основания. Если закон Ома отражает особенности взаимодействия потока заряженных частиц с материалом проводника со стороны ограничения скорости потока заряженных и ускоряемых электрическим полем частиц, то закон Джоуля - Ленца отражает это взаимодействие со стороны передачи энергии ускоренных электрическим полем заряженных частиц, материалу про­водника. Более наглядно эти моменты вскрываются в классической электронной теории элек­тро­проводности металлов (КЭТЭМ). Рассмотрим физику процессов, обусловливающих электросопротивление и джоулев нагрев в металлах, и выведем полученные опытным путем законы Ома и Джоуля - Ленца. Носителями тока в металлах являются коллективизированные (обобществленные) валентные электроны атомов. В узлах их кристаллической решетки металлов находятся положительно заряженные ионы, совершающие хаотические тепловые колеба­ния вокруг положений равновесия. В пространстве между ионами сравнительно свободно переме­щаются отрицательно заряженные электроны, образующие своего рода электронный газ, подчи­няю­щийся, согласно КЭТЭМ, статистике Максвелла - Больцмана.

П

ри наложении внешнего электрического поля с напряженностью на электрон действует сила = q , сообщающая ему ускорение а = /m = q /m. Фактором, ограничивающим рост скорости электронов и ответственным как за электросопротивление (электрическое трение, тормо­жение), так и за джоулев нагрев проводника электрическим полем, является рассеяние электронов (являющихся носителями тока в металлах) на разного рода дефектах, несовершенствах материала (хаотических колеблющихся ионах, примесях, вакансиях и т. п.). В результате такого рассеяния и осуществляется "сброс" скорости и кинетической энергии с ускоренных электрическим полем электронов. Электроны при этом тормозятся, материал же, оказывая сопротивление их потоку, и, принимая на себя энергию движения электронов, повышает свою внутреннюю энергию, нагрева­ется.

Усредненный характер зависимости скорости электронов от времени можно изобразить в виде пилообразного графика. Скорость электрона ускоренного приложен­ным к проводнику электрическим полем линейно возрастает до тех пор, пока электрон не "столкнется" с какого-либо рода неоднородностью кристалла, не рассеется на ней и не потеряет своей скорости и кинетической энергии. Статистиче­ски усредненное время свободного пробега (от соударения до следующего соударения) обозначено за .

В среднем можно считать, что электрон движется со скоростью  = _макс/2.

Так как _макс = а = qЕ/m, то  = qЕ/2m.

При перемещении с такой средней скоростью, через поперечное сечение S проводника за время t пройдет число N носителей, содержащееся в объеме проводника V = S t.

N = nV, где n - концентрация носителей (число их в единице объема). Они перенесут заряд

q_ = qN = qnV = qn  St.

Заряд же переносимый через единицу площади поперечного сечения за единицу времени, т. е. плот­ность тока, равна:

j = q_/St = qn  = qnqЕ/2m = (nq²/2m)Е = Е = Е/,

где коэффициент пропорциональности между плотностью тока и напряженностью Е есть удельная электропроводность  или обратное ей удельное электросопротивление 1/:

 = 1/ = nq²/2m.

Полученная связь между плотностью тока и напряженностью электрического поля и пред­ставляет закон Ома в дифференциальной форме: j = Е = Е/.

Для получения закона Джоуля - Ленца в дифференциальной форме, рассмотрим механизм нагрева проводника электрическим током. Такой нагрев, как правило, осуществляется в результате столкновений (рассеяния) электронов с хаотически колеблющимися ионами в узлах кристалличе­ской решетки, которым электроны и передают накопленную в ускоряющем их электрическом поле кинетическую энергию m²_макс/2. Электроны здесь играют роль своеобраз­ного трансформатора; воспринимая энергию электрического поля в виде своей кинетической энер­гии, они затем передают ее при соударениях на увеличение амплитуды и соответственно энергии тепло­вых хаотических колебаний ионов в узлах решетки.

3а единицу времени один электрон столкнется 1/ раз и передаст решетке энергию (m²_макс/2)(1/). Единице же объема будет передана (выделена) энергия: Р_уд = nm²_макс/2.

Подставляя в это выражение _макс = а = qЕ/m, получаем:

Р_уд = nm²_макс/2 = nm(qЕ)²/2m² = (nq²/2m)Е² = Е² = Е²/,

т. е. закон Джоуля - Ленца Р_уд = Е² = Е²/ - в дифференциальной форме, где  = 2m/nq².

Лекция 7. Взаимодействие проводников с током. Магнитное поле. Сила Ампера. Индукция магнитного поля.

Из опыта известно, что параллельные проводники с однонаправленными токами притягива­ются, а с разнонаправленными токами отталкиваются. Но это взаимодействие не является электро­статическим т. к. проводник с током в целом является электрически нейтральным и электростатиче­ского поля не создает. Поэтому и ввели представление о новом физическом поле, дополнительном к электростатическому и названном магнитным (МСП).

Нецентральный характер магнитостатического поля осложняет введение основной силовой характеристики МСП. В роли источников MСII могут выступать и элементы тока, и сами проводники с током, замкнутые контура (витки) с током, а также постоянные магниты. Основную силовую характеристику МСП, называемую индукцией , можно вводить различным образом, пользуясь разными (но взаимосвязанными) проявлениями МСП - воздействием его на точечный движущийся заряд, на элемент проводника с током, на замкнутый контур с током и др.

На практике распространение получил способ введения основной характеристики МСП на примере анализа ситуации воздействия его на пробный (достаточно малый, не возмущаю­щий самого МСП) замкнутый контур с током. Т. к. в противоположных частях замкнутого контура ток течет в противоположных направлениях, то на них со стороны МСП будут действовать силы противоположного направления, которые создадут вращающий момент , ориентирующий контур определенным образом в магнитном поле. Этот момент пропорционален силе  тока в контуре, его площади S и зависит от ориентации контура в МСП. Отношение же максимального вращающего момента М_макс, действующего со стороны МСП на пробный контур (малый виток с малым током), к его магнитному моменту (Р_м = S), не зависит ни от силы тока в контуре, ни от площади контура. И потому оно может служить в качестве силовой характеристики МСП самого по себе, независящей от характеристик пробного контура (в данной точке), называемой индукцией МСП:

В = М_макс/Р_м = М_макс/IS [Нм/Ам² = Н/Ам = Тл]

здесь Р_м = IS - магнитный момент контура с током - мера его взаимодействия с МСП.

М

агнитный момент рамки, контура с током является величиной векторной; его направление определяется по правилу буравчика, совпадая с направлением его поступательного перемещения при вращении его рукояти в направлении обтекания током контура: = IS где - единичная нормаль к контуру с током, направленная в соответствии с правилом правого винта.

В

ращающий момент, действующий на контур с током со стороны MCII, стремится развер­нуть контур так, чтобы его нормаль совпала с направлением силовых линий МСП. В общем случае, при произвольной ориентации контура с током относительно силовых линий МСП, вращающий его силами МСП момент может быть записан так:

М = М_максsin  = ВР_мsin 

Это выражение может быть записано в векторном виде:

= [ , ]   и  . Силовые линии МСП, т. е. линии вектора - такие, касательные к которым в каждой точке совпадают с направ­лением вектора .

Также как и в электростатике, основную силовую характеристику дополняют вспомогатель­ной, облегчающей расчет основной характеристики в неоднородных (здесь - в магнитном отноше­нии) средах. Терминологически в назва­ниях основных и вспомогательных силовых характеристик электростатического и магнитостатического полей имеет место несоответствие.

У ЭСП основная характеристика называлась напряженностью, а вспомогательная - индукцией (электриче­ским смещением), и связь между ними выражалась формулой = _о .

У МСП основная характе­ристика называется индукцией, а вспомогательная - напряженностью. Связь между ними выражается соотношением: = _о , где _о = 410^-7 Гн/м - магнитная постоянная, а  - маг­нитная проницаемость среды. Специфической особенностью магнитостатического взаимодействия является его не центральный характер и, соответственно, не потенциальный характер МСП. Силы МСП являются неконсер­вативными, их работа зависит от формы пути (перемещения) и не равна нулю по замкнутому контуру. Поэтому для МСП не вводится наряду с силовой скалярная энергетическая характери­стика, подобная потенциалу  в ЭСП.

Также как и для векторов и , для векторов и справедлив принцип суперпозиции, позволяющий находить характеристики результирующего МСП, созданного совокупностью источ­ников (движущихся зарядов, проводников с током, контуров с током) как векторную сумму или интеграл от соответствующих характеристик отдельных, элементарных источников:

_ =  _ ; _ =  _ , или _ =

Силовые проявления МСП. Действие МСП на проводник и контур с током и на движущуюся заря­женную частицу. Сила Лоренца.

Сила F, с которой МСП действует на движущуюся заряженную частицу, прямо пропорциональна ее заряду q, скорости  движения, индукции В и зависит от ориентации скорости частицы относительно направления силовых линий , задаваемой углом  = ( ^ ):

F = qВsin ( ^ ) = qВsin ;  = q[ ]

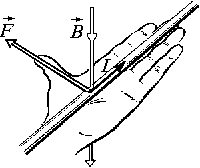
Эта сила перпендикулярна, как вектору скорости частицы, так и вектору индукции . Ее направление определяется правилом левой руки (для положительного знака заряда частицы): раскрытая ладонь располагается так, чтобы силовые линии MCП входили в нее, а четыре пальца были направлены по скорости частицы, тогда отогнутый большой палец укажет направле­ние силы.

Если заряженная частица влетает в МСП перпендикулярно его силовым линиям, то траек­торией частицы будет окружность с радиусом R, определяемым из условия:

F = F_макс = F_{ц с} = qB = m²/R  R = m/qВ и периодом Т вращения Т = 2R/ = 2m/qВ . Характерно, что период вращения частицы в магнитном поле не зависит от ее скорости.

Сила со стороны МСП является центростремительной, изменяющей лишь направление, но не значение скорости частицы.

При   /2 траекторией будет винтовая линия (спираль):

а)  = /2 б)   /2

Т. к. сила, действующая со стороны МСП на движущуюся заряженную частицу, перпендику­лярна ее скорости, то, не изменяя скорость частицы по численному значению, эта сила не совершает работы (не изменяет кинетическую энергию частицы). Поэтому, например, источники МСП (постоянные магниты и др.) могут длительно существовать, не разряжаясь, не уменьшая свою энергию.

В общем случае, при наличии как магнитного, так и электрического поля, результирующая сила, действующая на частицу равна: = q + q [ ] = q{ + [ ]} и называется силой Лоренца. Часто силой Лоренца называют ее магнитную составляющую q [ ].

П

ри помещении в МСП проводника с током на него дейст­вует сила, представляющая собой результирующую сил, действую­щих со стороны МСП на движу­щиеся в проводнике заряженные частицы (носители тока) и назы­ваемая силой Ампера.

Если поле (МСП) однородное, а проводник прямолинейный, то сила Ампера может быть выражена следующей формулой:

F_А = NF = NqВsin . Так как  = l/t, и Nq/t = I, то F_А = (Nql/t)Вsin  = ВIl sin ,

где q - заряд одной частицы (носителя тока); N - число носителей тока в проводнике длиной 1;

t - время прохождения заряженной частицей пути l.

С

ила Ампера направлена так же, как и сила, действующая со стороны МСП на отдельную положительно заряженную частицу, т. е. в соответствии с правилом левой руки. Здесь четыре пальца раскрытой левой ладони направляются по току в провод­нике.

В общем случае, когда МСП неоднородно, а проводник с током - криволинейный, можно записать выражение для элементарной силы Ампера - силы, действующей со стороны МСП на малый элемент тока который можно счи­тать прямолинейным, а магнитостатическое поле вокруг него - од­нородным. Тогда выражение для силы Ампера: F_А = BIlsin  при­менительно к элементу тока Idl примет вид dF = ВIdl sin . Оно может быть записано в векторном виде: = I[ ]. Полная же сила, действующая со стороны МСП на криволиней­ный проводник с током, запишется в виде интеграла по всем элементам тока (по всей длине провод­ника с током) от элементарных сил:

=

На любой замкнутый контур L с током результирующая сила со стороны однородного МСП c = const, равна нулю:

= = I = I[ = 0, т. к. = 0

Взаимодействие проводников с током.

Опытный факт силового действия друг на друга проводников с током (параллельные проводники с однонаправленными токами притягиваются, а с разнонаправленными токами – оттал­киваются) послужил в свое время основанием для введения представления о магнитном поле как посреднике, передающем силовое действие между телами, не соприкасающимися непосредственно. На полевом языке (описании) взаимодействие проводников с током интерпретируется как действие на каждый из проводников магнитного поля, создаваемого другим проводником.

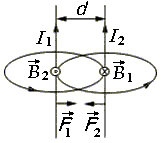
Рассмотрим взаимодействие двух бесконечно длинных параллельных, прямолинейных проводников с постоянными токами в них.

Каждый из проводников создает свое магнитное поле, основная силовая характеристика - индукция В которого, определяется выражением: В₁ = _оI₁/2d. Это поле действует на другой проводник с силой Ампера F_А2 = B₁I₂lsin  = _оI₁I₂l/2d. На единицу длины проводника приходится сила Ампера, равная: F_А/l = _оI₁I₂/2d.

П

о третьему закону Ньютона, силы, с которыми про­водники с током (или их магнитные поля) действуют друг на друга, равны по величине и противоположны по направле­нию. Т. к. сило­вые линии МСП проводника с током направ­лены согласно правилу правого винта (буравчика) и представляют собой концентрические окруж­ности вокруг проводника, то, применив правило левой руки для силы Ампера, убеждаемся, что при одно­направленных токах (как это показано на рисунке), силы взаимодействия носят характер при­тяже­ния.

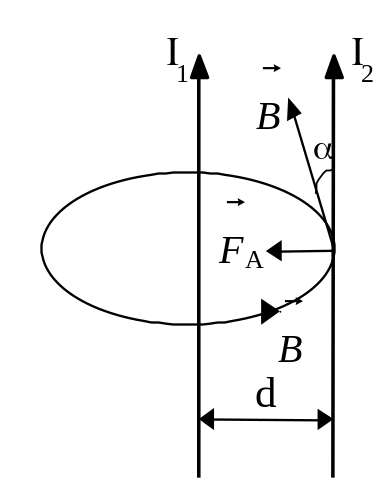
Магнитное взаимодействие проводников с током положено в основу определения основной электрической единицы в СИ - единицы силы тока - ампера. За ампер принимается сила такого тока в прямолинейных параллельных проводниках, находящихся в вакууме на расстоянии 1 м друг от друга, при котором сила их взаимодействия в расчете на единицу длины равна F_А/l = _о/2 = 210^-7 Н.

Контур (рамка) с током в однородном внешнем МСП.

Основную силовую характеристику магнитного поля - индукцию В мы вводили на примере опытного факта, заключающегося в действии МСП на малую рамку с током в виде вращающего момента (момента сил МСП). Такими силами являются силы Ампера. Получим выражение для вращающего момента, действующего со стороны МСП на прямолинейную рамку с током силой , исходя из силы Ампера.

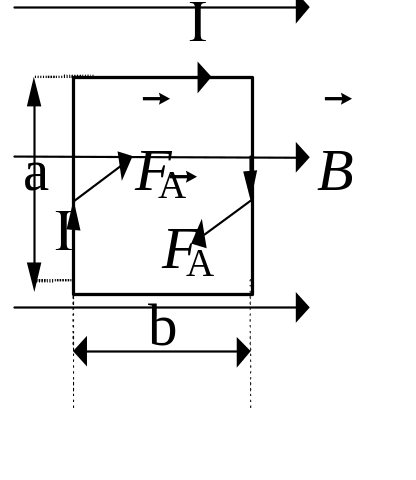
На стороны рамки, параллельные силовым линиям МСП сила Ампера не действует (ее значение равно нулю).

На перпендикулярные стороны сила Ампера действует в про­тивоположных направлениях (вследствие противоположного направления тока в них), благодаря чему и возникает вра­щающий момент М - произведение силы на плечо ее дейст­вия:

М = 2F_Аb/2 = 2Ваb/2 = BS = Bр_м

где: S = аb - площадь рамки с током; р_м = S - магнитный дипольный момент рамки с током.

В общем случае, при   /2, М = р_мВsin  или, в векторной форме = [ ]

Магнитное поле стремится сориентировать рамку с током так, чтобы ее магнитный момент был направлен вдоль силовых линий вектора . При  = 0 рамка сориентирована магнитным полем и испытывает с его стороны только растягивающее воздействие.

Для того чтобы угол  между векторами и изменить на d, нужно совершить работу dА = Мd = р_мВsin  d = - р_мВd (cos ) = - dW_м  W_м = - р_мВcos  + const. Значению  = 0 соот­ветствует минимум потенциальной энергии W_м магнитного взаимодействия.

Лекция 8. Основные теоремы магнитостатического поля. Энергия и объемная плотность энергии магнитостатического поля.

Так же как и для ЭСП, для МСП - как векторного поля, важными теоремами, лежащими в основе методов расчета характеристик МСП, являются теоремы о циркуляции и о потоке вектора поля (вектора или вектора ).

Вследствие не потенциального, вихревого характера МСП, для него не удается просто и наглядно получить эти теоремы исходя из основного закона, устанавливающего фундаментальный характер сил магнитостатического взаимодействия на элементарном уровне (как это было в электро­статике - из закона Кулона).

С

некоторым приближением, условностью, в качестве отношения, аналогичного получае­мому из закона Кулона выражению для напряженности поля точечного заряда, может служить закон Био - Савара - Лапласа. Этот закон устанавливает силу МСП, создаваемого элементарным источни­ком - элементом тока на удалении r от него:

d Н = dl sin/4r² или dB = _оdlsin /4r²

где угол  - угол между векторами и .

В векторной форме закон Био - Савара - Лапласа принимает следующий вид:

d = [ ]/4r³ или

= _оd = _о[d ]/4r³

Вектор перпендикулярен как вектору так и вектору и направлен в сторону, опреде­ляемую правилом векторного произведения, или правилом буравчика (правого винта): - вращая буравчик рукоятью в плоскости векторов [ ] в направлении протекания тока, получим совпадение поступательного перемещения буравчика с направлением вектора индукции МСП.

Закон Био – Савара - Лапласа носит дифференциальный характер, и полную индукцию В_ или напряженность Н_ МСП в данной точке, создаваемую всем проводником с током, находят путем интегрирования, используя принцип суперпозиции:

_ =  _ или _рез =

Рассмотрим некоторые примеры применения закона Био - Савара - Лапласа для расчета характеристик МСП, создаваемого проводниками (с током) разной формы.

1) прямолинейный проводник с постоянным током.

Д

ля нахождения характеристик результирующего МСП, создаваемого прямолинейным проводником с током постоянной силы  на расстоянии а от него, выберем на проводнике элемен­тарный отрезок и запишем для него закон Био – Савара - Лапласа. Векторы элементарной индукции от разных элементов проводника с током сонаправлены и векторное суммирование (интегрирование) сводится к арифметическому. Полную индукцию В от всего проводника определим путем интегрирования; для этого три переменные: , r и  в законе Био – Савара - Лапласа: сведем к одной, удобнее всего к :

r = а/sin; [ ] = dl r sin  = r²d. Подставляя их под интеграл, произведем интегрирование; переменная  для проводника изменяется в пределах от ₁ до ₂.

dВ = _оdlsin /4r² = _оIsin² аdsin /4а²sin²  = _оIsin d/4а.

В = = (_оI/4а) = (_оI/4а)(cos ₁ - cos ₂)

Н = В/_о = (I/4а)(cos ₁ - cos ₂) [Н] = А/м.

В

результате получили довольно простые выраже­ния для индукции и, особенно для напряженности МСП, создаваемого бесконечно длинным прямолинейным провод­ником с постоян­ным током I на удалении а от него.

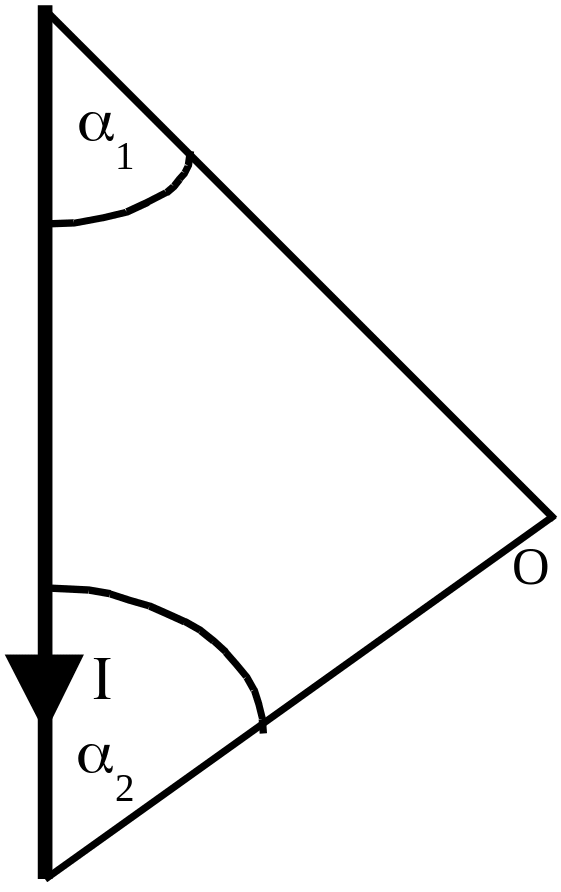
Углы ₁ и ₂ - это углы, под которыми из концов проводника видна точка, в которой ищется индук­ция и/или напряженность МСП. 2) Если проводник имеет бесконечную длину, то для него можно повторить все вышесказанное и проделанное с той лишь разницей, что пределы интегрирования (₁- ₂), характерные для конеч­ного проводника, следует заменить на пределы (0 – ). При этом очевидно, результат получается следую­щим:

В = _оI/2а и Н = I/2а

3) круговой проводник с постоянным током.

Р

ассчитаем вначале В и Н в центре кругового тока силой I и радиусом R. Так как   = R и  d , т. е.  = /2, то dH = Idl/4r² = Idl/4R² 

Н = = = (I/4R²)2R = I/2R и

В = _оН = _оI/2R

Силовые линии МСП обвивают проводник с током в направлении, определяемом правилом буравчика (правого винта): при вкручивании буравчика по направлению тока, вращательное пере­мещение рукояти задает ориентацию силовой линии.

В качестве второго важного метода расчета характеристик МСП выступает теорема о цирку­ляции вектора (или вектора ).

Если у ЭСП, которое имело потенциальный характер, циркуляция - работа по перемещению единичного заряда по замкнутому контуру, равнялась нулю, то у МСП, вследствие его не потенци­ального, вихревого характера, циркуляция векторов и отлична от нуля. Например, для прямо­линейного бесконечного проводника с постоянным током, как мы уже рассматривали, она может быть представлена в виде:

= = = = (I/2а) = (I/2а)2а = I

= = = В = (_оI/2а)2а = _оI

Ц

иркуляция вектора для прямолинейного бесконечного проводника с током численно равна силе тока в этом проводнике = I. Если замкнутый контур L охватывает N токов, то можно сформулировать общую теорему о циркуляции вектора

циркуляция вектора по некоторому контуру L равна алгебраической сумме токов, охватываемых этим контуром:

= I_

Циркуляция вектора по любому контуру также не зависит ни от размеров, ни от формы контура, а с точностью до постоянного множителя _о определяется алгебраической суммой токов, охватываемых данным контуром:

= = _оI

Неравенство нулю циркуляции векторов и говорит о том, что силовые линии МСП (линии векторов и ) являются замкнутыми (образуют вихри), в отличие от ЭСП, где силовые линии имели начало (на положительных зарядах) и конец (на отрицательных зарядах или в беско­нечности).

Другим выражением этой вихревой, не потенциальной природы МСП является равенство нулю потока вектора (и ) через любую замкнутую поверхность.

Э

лементарный поток dФ_в = = ВdScos  = В_ndS пропорционален числу силовых линий, пронизывающих площадку .

П олный поток Ф_В вектора через любую замкнутую поверхность S равен нулю, т. к. сколько силовых линий входит в нее, столько и выходит из нее (в силу их замкнутого характера):

Ф_в = = = 0

П

рименим теорему о циркуляции вектора для нахождения характеристик МСП соленоида - длинной катушки с большим числом N витков. Возьмем циркуляцию вектора через замкнутый контур L  АВСDА, проходящий через ось соленоида АС:

= I_ = NI

При удалении наружного участка D контура на , где МСП соленоида стремится к нулю, получим:

= + = = Hl = IN  Н = IN/l

Напряженность МСП внутри соленоида равна числу ампервитков, приходящихся на единицу длины l соленоида. Подобная формула справедлива и для напряженности магнитного поля тороида - катушки «свернутой в кольцо, в бублик». Длина l у тороида равна 2R, где R - его срединный радиус.

Индуктивность контура и соленоида.

Ток, протекающий по контуру (витку), порождает МСП, которое пронизывает и поверх­ность, ограниченную этим контуром. Контур с током находится в собственном магнитном поле, и его поверхность пронизывается eгo же потоком Ф_В. Чем больше ток  в контуре, тем больше поро­ждаемый им поток Ф_В.

Если контур содержит N витков, т. е. имеем катушку, то результирующий поток Ф_В = NФ = , сцепленный с витками катушки, называется потокосцеплением. В отличие от потока Ф, потокосцепление  характеризует «собственное» магнитное поле, т. е. поле, создаваемое током самого контура (катушки), поверхность которого оно пронизывает.

С ростом силы тока в контуре (катушке) прямо пропорционально растет и порождаемое им потокосцепление, т. е.  ~ I. Отношение же /I = L, называемое индуктивностью контура (катушки), не зависит по отдельности ни от силы тока I в контуре, ни от сцепленного с ним потока , а определяется размерами и формой контура, числом витков в нем и магнитной проницаемостью среды :

L = /I = NФ/I = NBS/I = N_оINS/Il = _оN²S/l = _оn²Sl, где n = N/l - число витков на единицу длины катушки, S - площадь ее поперечного сечения.

Индуктивность катушки является магнитным аналогом емкости конденсатора. Для соленоида индуктивность выразится следующей формулой:

L = /I = _оN²S/l = _оn²Sl.

Единица индуктивности - генри: Гн = 1 Вб/1А

Работа перемещения проводника и контура с током в магнитном поле.

Рассмотрим следующий мысленный опыт: в однородном МСП расположен прямолинейный контур с постоянным током; одна из сторон контура образована подвижной проводящей перемычкой длиной l. Вычислим работу, которая совершается при перемещении подвижной перемычки на расстояние d. Важно отметить, что непосредственно на перемычку действует сила со стороны МСП - сила Ампера, но работу по перемещению перемычки совершает не МСП, а источник тока, поддерживаю­щий постоянной силу тока в цепи:

А₁₂ = Fd = Bld = BS = Ф_В

Получили, что работа по перемещению проводника с током в магнитном поле равна произведению силы тока в контуре на величину потока магнитной индукции (число силовых линий МСП), который пересекает проводник при своем перемещении: А₁₂ = Ф_В

Поток Ф_В можно рассматривать как разность двух значений Ф_В1 и Ф_В2, которые представляют собой потоки вектора индукции МСП, пронизывающие замкнутый контур АВСDA и АBМNA при двух разных положениях перемычки. И тогда работу по перемещению проводника (и контура) с током в магнитном поле можно записать в форме, подобной таковой для работы перемещения заряда в элек­тростатическом поле:

А₁₂ = (Ф_В2 - Ф_В1). В электростатике было А₁₂ = q(₁ - ₂).

Полученное выражение для работы перемещения проводника с током в магнитном поле оказывается справедливым и для более общего случая - перемещения в магнитном поле всего замк­нутого контура с током в целом, независимо от степени однородности магнитостатического поля и вида движения контура - поступательного, вращательного или совместного, и способа изменения магнитного потока.

Работу по перемещению контура с током в магнитном поле можно определить как численно равную произведению силы тока в контуре на изменение потока магнитной индукции (Ф_В2 - Ф_В1), пронизывающего контур в конечном и начальном положениях.

Причиной возникновения индукционного тока в контуре является сила Лоренца, действующая на заряды в движущемся проводнике. Это означает, что сила Лоренца играет роль сторонней силы. Напряженность поля сторонних сил равна: . Вектор напряженности поля сторонних сил для электронов и ионов направлен в одну сторону (в сторону действия силы Лоренца на положительные заряды – ионы).

Электродвижущая сила, создаваемая полем сторонних сил, называется электродвижущей силой индукции и обозначается . Напомним, что электродвижущая сила равна работе сторонних сил по перемещению единичного заряда. Поскольку сторонняя сила возникает только в движущейся перемычке длиной l, то э.д.с. индукции равна: . Для определения знака э.д.с. индукции выберем нормаль к контуру. Пусть нормаль к контуру направлена за чертеж. Направление совпадает с направлением обхода контура. Направление обхода контура определяется правилом правого винта: поступательное движение винта совпадает с направлением нормали к контуру, а направление вращения головки винта совпадает с направлением обхода контура. В данном случае направление обхода – по часовой стрелке, поэтому вектор на перемычке направлен вниз. Направлением вектора магнитной индукции в данном случае совпадает с нормалью к контуру, а проводник движется вправо, поэтому напряженность поля сторонних сил направлена вверх вдоль проводника. Таким образом, угол между вектором и равен 180⁰, следовательно . Подставляя в последнее выражение , получим: . По определению скорость равномерного движения проводника равна , где х - изменение координаты проводника вдоль направления его движения. Поэтому:

.

Таким образом, в случае равномерного движения проводника в однородном магнитном поле, в проводнике возникает э.д.с., равная Е_ = - Ф/t.

В общем случае для нахождения э.д.с. индукции в контуре в любой момент времени нужно найти предел отношения Ф/t при условии неограниченного уменьшения промежутка времени (t  0). При известной зависимости от времени магнитного потока через контур предел этого отношения определяется как производная от магнитного потока по времени:

Индукционные токи могут возникать и в неподвижных проводниках.

Энергия и объемная плотность энергии магнитного поля.

По аналогии с выводом выражения для энергии электрического поля рассмотрим магнитный аналог конденсатора - соленоид - длинную тонкую катушку длиной l, обладающую большим числом витков N, площадью поперечного сечения S и индуктивностью L. Пусть по катушке протекает ток силой I и катушку пронизывает результирующий магнитный поток (потокосцепление)  = Ф_В = ВSN = _оIN²S/l.