6. Термодинамика открытых систем. Течение газов

Уравнения первого закона термодинамики для закрытой системы dq = du +dl=du +pdv, dq=di-vdp дополняются компонентами ,учитывающими: работу против внешних сил –работу проталкивания газа по каналу dl^/ и изменение внешней кинетической энергии – располагаемую работу (dw² /2 ). Уравнение первого закона термодинамики для потока газа ,когда еще совершается и полезная техническая работа dl_Т ( не связанная с деформацией границ системы)

dq = du +dl^/ + d (w² /2) + dl_Т = du + d(pv) +d(w² /2) + dl =di +d(w² /2) +dl_Т . ...(6.1)

Из сопоставления уравнений первого закона для закрытых и открытых систем видно ,.что

dl =dl^/ +d(w² /2), ...(6.2)

т. е. работа расширения dl затрачивается на проталкивание газа по каналу -dl^/ и на разгон потока , на увеличение скорости – d(w² /2). После преобразований оказывается ,что

d(w² /2) = - vdp , wdw = - vdp , …(6.3)

значит для увеличения скорости необходимо понижение давления ,и наоборот, для повышения давления – уменьшение скорости.

Энтальпия i рабочего тела в потоке играет ту же роль, что и внутренняя энергия u неподвижного рабочего тела . Энтальпия включает в себя внутреннюю и потенциальную энергии рабочего тела .

Для разгона потока в тепловых двигателях и машинах достаточно коротких каналов . Время нахождения рабочего тела в них мало ,т.к. скорости истечения велики , теплообмен между рабочим телом и стенками канала практически не успевает произойти и может считаться адиабатным.

При адиабатном процессе уравнение первого закона термодинамики принимает вид

di + d(w² /2) = 0 …(6.4) и после интегрирования получается ,что при скорости входа в канал много меньше скорости выхода из него (w₁ w₂ , т. е.практически можно cчитать w₁ ≈ 0 ) скорость истечения

w₂ ≈ 2(I₁ –i₂) = (2к/k-1) p₁ v₁[ 1 – (p₂ /p₁ )^(k-1)/k ], …(6.5) где р₁ и р₂ - давления в начале и конце процесса расширения .

Массовый расход газа m = F w₂/v₂ ( F – площадь выходного сечения сопла ). Тогда , c учетом уравнения адиабаты р₂ v₂^k = p₁ v₁^k и уравнения (6.5) ,

m = F ( 2k/k-1)(p₁ /v₁ )[ (p₂ /p₁)^2/k - (p₂ /p₁) ^(k+1)/k ]. ... (6.6)

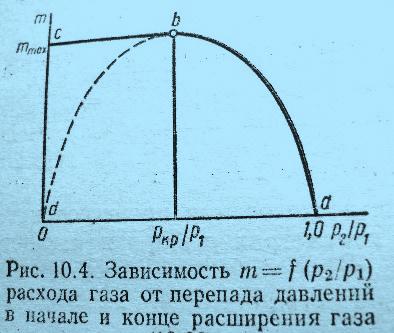В соответствии с (6.6) график зависимости m = f(p₂ /p₁ ) должен на Рис.10.4. иметь вид a – b –d. Но в действительности расход газа изменяется по a –b –c , т.к. его давление на выходе из суживающегося сопла не может стать меньше критического.

Следуя гипотезе Сен-Венана (Адемар Жан – Клод Барре де Сен- Венан, Парижская академия наук ,1839г.): Нельзя получить давление ниже р_кр соответствующего максимальному расходу через сопло как бы не понижать давление на выходе p₂ = p_кр (или как бы не повышать его на входе).

Критическое отношение давлений при которых расход газа максимален

P₂ /p₁ = p_кр /p₁ =( ( 2/(k +1 )) ^K/(k-1) , ...(6.7) а критическая скорость истечения

w_кр = кp_кр v_кр . …(6.8)

Из физики известно ,что скорость распространения звука в среде с параметрами p, v равна

a = kpv , …(6.9) …(6.9) а для идеального газа (pv = RT) , т. есть a = kRT.

Из (6.8) и (6.9) следует , что критическая скорость истечения через суживающееся сопло w_кр равна местной скорости звука а .

(Скорость звука в воздухе а = 20,1 , при Т ≈ 300К ≈ 320 м/с, в воде и твердых телах ≈1500 м/с , но в барботируемой среде ( вода + воздух) - ≈20м/с ,!!!).

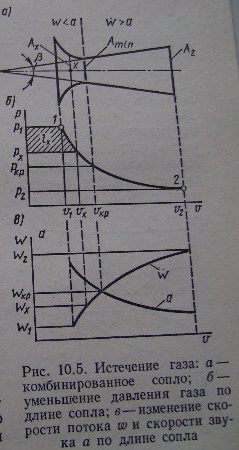
В суживающихся соплах нельзя получить скорость потока, превышающую местную скорость звука. Это достигается ,например ,в соплах специальной формы . После дифференцирования уравнения неразрывности F = mv/w и преобразований получается ,что dF/F = (M² – 1)dw/w , т. е.

(M² – 1)dw/dx =w/F (dF/dx), …(6.10)

где М = w/a - критерий Маха ,отношение скорости газа w к скорости звука в данном сечении . ( На сверхзвуковых самолетах стоят так наз. “махометры”).

Если М <1 , то и dF<0 ( сопло сужается) и наоборот, при М >1 оно должно расширяться.

Для получения сверхзвуковой скорости потока сопло должно быть комбинированным: сначала – суживающимся ,затем – расширяющимся. Комбинированное сопло предложил шведский инженер К. Г. Лаваль (1845 -1913г.г.) для паровых турбин (кроме того, он был известен и в области производства серной кислоты, доильных машин, циклонных печей для выплавки чугуна, в области обезвоживания торфа …).

Максимальный расход газа через сопло Лаваля ( по имени автора ) определяется поперечным сечением самой узкой части сопла , в месте перехода суживающейся части в расширяющуюся.

Выбор профиля сопла здесь не рассматривается ,только угол на Рис .10.5. должен быть не более (10 -12)⁰ ( для устранения отрыва газа от стенок сопла ) , а длина сопла для сверхзвуковой части определяется площадями его самой узкой части и выхода .

Эффект комбинированного сопла имеет и дополнительный подвод тепла и/или массы в докритической ( дозвуковой) области течения газа и отвод - в сверхкритической области.