Работа № 4 исследование условий теплообмена в термокамере

1. ЦЕЛЬ РАБОТЫ. Изучение процесса теплового воздействия на модель в условиях конвективного теплообмена.

2. ЗАДАНИЕ. Экспериментально определить значение коэффициента тепло-отдачи ““ в полезном пространстве одной из испытательных камер в режиме охлаждения.

3. ОСНОВНЫЕ СВЕДЕНИЯ. Тепловое воздействие на тело определяется законом изменения температуры внешней среды во времени и интенсивностью теплообмена между телом и окружающей средой.

Коэффициент теплоотдачи  является коэффициентом пропорциональности между тепловым потоком, поступающим в тело, и перепадом температур между средой и поверхностью тела (t_ср.-t_пов.)

q=(t_ср.-t_пов.), (1)

причем =_т+_л+_к. (2)

Коэффициент кондуктивного теплообмена _т определяется теплопроводностью среды (воздух) и размерами исследуемого объекта. Он мал, например, для шара при естественной конвекции

, (3)

где

Nu - критерий Нуссельта;

D - диаметр шара;

_ср - коэффициент теплопроводности воздуха;

Коэффициент лучистого теплообмена _л не связан с режимом движения воздуха

, (4)

где

с₀=5,67 Вт/м²К⁴ - коэффициент излучения абсолютно черного тела (с₀=₀10^-8, ₀- постоянная Стефана-Больцмана);

_пр - приведенная степень черноты системы исследуемый объект-окружающее пространство, принимается 1);

Т_ср, Т_пов. - абсолютные температуры среды и поверхности тела, К.

Коэффициент конвективного теплообмена _к зависит от многих трудноучитываемых факторов и, в первую очередь, от режима движения воздуха вокруг изделия (естественная, вынужденная, смешанная конвекция). Поэтому определяют экспериментальным путем суммарный коэффициент теплоотдачи  экспериментальным путем для интересующих условий.

4. Методические указания по выполнению работы

4.1. Коэффициент теплоотдачи определяется методом калориметрирования термически тонкого тела, в котором градиентом (перепадом) температур по толщине можно пренебречь (значение критерия Био Bi=R/ 0,1;  - коэффициент теплопроводности материала; R - характерный размер).

Из уравнения теплового баланса при отсутствии градиента температур,

, (5)

где:

 - время;

t_ср=t_ср() - температура среды;

t_т= t_т() - температура модели;

- темп охлаждения; (6)

F, V - площадь поверхности и объем модели;

с,  - удельная теплоемкость, плотность материала модели.

Решение уравнения (5)

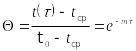(7)

(t₀ - начальная температура модели).

В полулогарифмических координатах ln-m это уравнение прямой. Если m=const, то в узком диапазоне температур =const. Темп охлаждения определяется обычным образом (см. работы 2, 3),

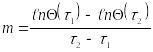, (8)

как тангенс угла наклона прямой логарифма безразмерной температуры.

4.2 Работа проводится на модели с условным индексом АГСВ-1. Модель представляет собой полый шар на подвеске “струне”. Его наружный и внутренний диаметры D=0,3 м и d=0,26 м, материал - сталь 45, масса - 34 кг; удельная теплоемкость и коэффициент теплопроводности материала модели с=0,469 кДж/кгК (0,11 ккал/кгК) и = 45,8 Вт/мК.