Метод регулярного теплового режима первого рода

Температурное поле в теле зависит от его геометрической формы, размеров, начального теплового состояния и условий теплообмена тела с окружающей средой. По истечении некоторого промежутка времени, определяемого условием критерий Фурье , ряд в решении

, n=1,2,3,… (3)

(t₀=t(r,=0)=const - начальная температура)

быстро сходится и все члены ряда, начиная со второго, становятся малыми по сравнению с первым, и распределение температуры во времени для всех точек тела может быть выражено первым слагаемым

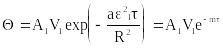(4)

Причем, постоянные A₁, U₁, ₁ - определяются геометрией, размерами, условиями теплообмена и не зависят от времени. Такое тепловое состояние тела названо регулярным (упорядоченным) режимом первого рода. (Величины А_n, V_n, _n представлены на стр. 63 /2/ и в /3/ , или в разделе I сборника.

Величина час^-1 носит название темпа охлаждения. Для шара R - наружный радиус, для пластины половина ее толщины. Величина ₁ является функцией критерия Био Bi=R/, поэтому m=m(a,,,R,r), т. е. темп охлаждения зависит от физических свойств, геометрической формы и размеров тела, а также от условий теплообмена тела с окружающей средой.

Темп охлаждения характеризует относительную скорость изменения температуры тела во времени. Если продифференцировать (4) по времени, то

, (5)

т.е. относительная скрость изменения температуры при переходе от одной точки тела к другой остается постоянной. Поэтому изменения температуры со временем для различных точек тела выражаются системой параллельных линий, если закон регулярного режима графически представить в координатах ln-, исходя из соотношения

ln=lnA₁V₁-m.

Темп охлаждения характеризует угловой коэффициент этих параллельных линий

. (6)

Определение коэффициента температуропроводности

Для критерия Био Bi= (практически Bi100), t_ср= const

a=km_~ , (7)

где k=(2R/)² для неограниченной пластины толщиной 2R;

k=(R/)² для сплошного шара радиуса R (для полого шара взамен R берется его толщина).

Для случаев Bi100 используется метод двух точек, справедливый для любых конечных значений критерия Био. В нем используется важнейшее свойство регулярного теплового режима: температурное поле во времени остается подобным самому себе. Следовательно, отношение температур в двух произвольных точках “а” и “с” равно постоянной величине, не зависящей от времени

. (8)

Очевидно, что

b=e^-y, y=(ln_a-ln_c). (9)

4. Методические указания по выполнению работы

Работа со сферической моделью сводится к следующим операциям:

4.1. Подготовка модели, установка термоэлектрических преобразователей ТХК.

После проверки схемы измерения температуры модель помещается в холодильную камеру, предварительно выведенную на выбранную температуру t_ср.

На протяжении всего периода охлаждения выполняются условия: t_ср=const, =const, где -коэффициент теплообмена модели с воздушной средой камеры (10 Вт/м² К).

4.2. В процессе охлаждения определяется зависимость t=t() в различных точках конструкции.

4.3. Переход к безразмерной температуре

4.4. Определение периода регулярного режима ln=f()

4.5. Определение темпа охлаждения.

,

где ₁, ₂ - температура в моменты времени ₁ и₂.

4.6. Определение коэффициента температуропроводности для сферического тела.

Оценивается значение критерия Био Bi=R/, при Bi100 находится , затем ₁ из уравнения sin₁/₁=b. Коэффициент температуропроводности определяется из выражения а=mR²/₁², при Bi100 коэффициент температуропроводности находится из (7), как а=m_~(R/)². (Для полого шара взамен R берется его толщина).

4.7. Сравнение полученного значения “а” с расчетным.

(м²/час)

по табличным данным плотности  и удельной теплоемкости с_ материала модели.

4.8. Оценка погрешности.

Работа заканчивается выводами.

РАБОТА № 3

НЕСТАЦИОНАРНЫЙ МЕТОД ИССЛЕДОВАНИЯ ТЕПЛОВЫХ СВОЙСТВ ВЕЩЕСТВА

1. ЦЕЛЬ РАБОТЫ. Определение температурных напряжений в полой сфере при ее охлаждении (нагреве).

2. ОПИСАНИЕ МОДЕЛИ. Модель состоит из двух сложенных вместе полых полусфер. По торцу деталей установлены четыре термопары ТХК.

Материал полусфер имеет следующие характеристики:

коэффициент линейного расширения =10010^-7 К^-1;

модуль упругости I^го рода Е=0,210⁶ кГ/см²;

коэффициент Пуассона =0,35.

2. Кольцевые напряжения на наружней и внутренней поверхностях сферы максимальны и переменны во времени

,

где

a, b=R - внутренний и наружный радиусы сферы;

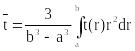- среднеинтегральная температура сферы.

3. Для определения t находится распределение температуры по слоям сферы в различные моменты времени.

С этой целью на торце полусферы установлены термопары на координатах

i=1,2,3,...,n (эти координаты соответствуют условию мысленного разбиения полой сферы на n равных по объему сфер, а затем каждой из них еще на две, равных по объему).

Для четырех точек измерения n=4, а=90 мм, b=145 мм, r₁=101 мм, r₂=117 мм, r₃=130 мм, r₄=140 мм.

4. Среднеинтегральная температура определяется как среднеарифметическое

.

5. Напряжения на наружней поверхности при охлаждении растягивающие, на внутренней - сжимающие, при нагреве - наоборот. Они определяются формулой раздела 2. Их зависимость во времени следует построить графически, затем найти моменты времени, соответствующие их максимальным значениям.

6. Оценка погрешности.

Работа заканчивается выводами.