4. Методические указания по выполнению работы

Собрать плоский прибор для измерения коэффициента теплопроводности () твердых пластинчатых материалов.

Образцы исследуемого материала 20020010.

Резистивный нагреватель - лента нихрома толщиной S=0,05 мм.

Дополнительная термоизоляция - асботкань (асбобумага) толщиной S=35 мм.

Холодильник - буферная теплоемкость, пластина из алюминиевого сплава или стали толщиной S=20-30 мм.

Условия симметрии плоского прибора позволяют вести расчет коэффициента теплопроводности по уравнению

где

_р - расчетная толщина образца с учетом поправки на глубину заделки термопар, [м];

q=Q/2F - удельный на единицу площади тепловой поток, Вт/м²;

Q=IU (I - сила тока в нагревателе, А; U - падение напряжения на расчетной длине нагревателя, В);

t=(t₁-t₂) - перепад температур, С.

Определение коэффициента теплопроводности  осуществляется в двух опытах при различных режимах питания электронагревателя модели.

Номер опыта	Сила тока I	Падение напряжения U	Общий тепловой поток, Q	Перепад температур t=t1-t2	Удельный тепловой поток, q	Коэффициент теплопроводн.	Относительная погрешность 
1
2

_р= м, F= м².

Образцы исследуемого материала изготавливаются в виде пластин прямоугольной формы. В нашем случае размеры пластин 0,18  0,15 м.

С целью получения одномерного теплового потока при выборе размеров плоского образца применительно к телам со сравнительно малой величиной коэффициента теплопроводности 23 Вт/м С необходимо выполнить соотношение где L - размеры пластины.

Если взять пластины толщиной =810^-3 м, то это условие выполнится для размера любой их стороны.

Одномерность теплового потока в конструкции прибора обеспечивается тонким нагревателем - 0,05 мм. Потери тепла с боковой поверхности нагревателя минимальны, а потери с боковых поверхностей образцов перекрываются дополнительной изоляцией.

Для практически полной симметрии тепловых потоков прибор, в отличие от представленного на рисунке выше, должен быть установлен в вертикальном положении.

Относительная погрешность определения коэффициента теплопроводности

, (6)

где

I, U, _p, t - абсолютные погрешности определения тока, падения напряжения, толщины и разности температур ( согласно классу примененных приборов).

Работа заканчивается выводами.

Работа № 2 нестационарный метод исследования тепловых свойств веществ

1. ЦЕЛЬ РАБОТЫ. Изучение специфики исследования теплофизических свойств материалов в нестационарных во времени температурных условиях.

2. ЗАДАНИЕ. Экспериментально определить коэффициент температуропровод-ности твердого материала нестационарным методом.

3. ОСНОВНЫЕ СВЕДЕНИЯ. При исследовании тепловых параметров методом нестационарного теплового потока используются решения дифференциальных уравнений теплопроводности

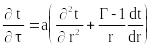(1)

при различных граничных условиях, например, третьего рода

(2)

где t=t(r,) - температура на координате r в момент времени ;

t_R, t_ср - температура поверхности и внешней среды;

, a=/c - коэффициенты теплопроводности и температуропроводности (с - удельная теплоемкость, - плотность);

 - коэффициент теплоотдачи;

Г - коэффициент формы (1-пластина, 2-цилиндр, 3-шар).

Обычно эти решения, как и в случае теплопроводности при установившемся тепловом режиме, получают применительно к телам простой геометрической формы и для определенных граничных условий. При этом наблюдаются различные закономерности для зависимости температурного поля от времени. В начальный период эти зависимости отличаются сложным характером и математически обычно выражаются бесконечными рядами.

В последующей, основной стадии процесса теплопроводности, изменение температуры во времени приобретает упорядоченный характер и математически описывается проще при условии, что основная стадия процесса теплопроводности будет в эксперименте при постоянных граничных условиях, когда коэффициент теплоотдачи и температура среды не меняются во времени (регулярный режим первого рода).

Нестационарные методы позволяют избежать необходимости измерения тепловых потоков, что связано со значительными трудностями особенно при высоких температурах. Нестационарные процессы, как правило, являются быстро протекающими во времени, и не требуют значительного времени на предварительную выдержку образцов при определенной температуре.