6.Теплообменные аппараты

Теплообменники – устройства для передачи тепла от одной среды к другой. По принципу действия условно подразделяются на рекуперативные, регенеративные и смесительные. В рекуперативных, наиболее распространенных, тепло передается через разделяющую среды твердую стенку; в регенеративных – за счет периодического аккумулирования и отдачи тепла каким-то промежуточным теплоносителем, обычно твердым телом; смесительные теплообменники – вряд ли нуждаются в объяснениях (это, например, бытовой кран горячей и холодной воды, где не требуется площадь теплообмена).

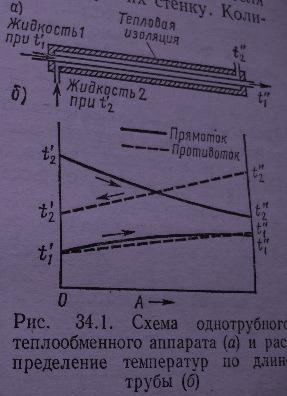
В рекуперативном теплообменнике при входе в него температура греющей среды t₁^/уменьшается по пути следования и на выходе из него падает до t₁^//, а нагреваемой среды - растет с t₂^/ до t₂ ^//. Или, наоборот, как это представлено на рисунке справа .

Рекуперативные теплообменники делятся на прямоточные, противоточные (простейшие - типа труба в трубе), перекрестного хода, более сложные со смешанными токами теплоносителей.

В любом случае, уравнения теплопередачи и тепловых балансов сохраняют свои силы ( для уравнений тепловых балансов - произведение расходных масс на температуры постоянно)

Q=k∆t_срА, …(54)

Q=-G₁∆i₁=G₂∆i₂ , …(55)

где Q – количество передаваемого тепла; G – расходы теплоносителей; ∆i – изменения их энтальпии , т. е. произведения теплоемкостей на температуры; k – cредний по пути следования коэффициент теплопередачи; A – расчетная поверхность теплообмена; ∆t_ср - средний температурный напор ( средняя разность температур между теплоносителями).

При прямотоке и противотоке, опуская промежуточные известные в популярных учебных изданиях выкладки

∆t_ср = (∆t_б - ∆t_м) /ln(∆t_б /∆_м) , …(56)

где ∆_б - разность температур теплоносителей на том конце поверхности теплообмена , где она больше; ∆_м – на другом конце поверхности теплообмена. При других схемах движения теплоносителей это уточняется поправочными коэффициентами, что здесь из-за ограниченного объема изложения не может быть рассмотрено, но это есть в специальной литературе.

Коэффициент теплопередачи k находится по обычным формулам для плоских поверхностей или круглых труб (шаров, если надо) , но еще и с учетом R_заг – термических сопротивлений от загрязнений с обеих сторон стенки ( накипь, сажа и пр.).

Тепловые расчеты есть проектные (конструктивные), гл. обр. для определения площади поверхности теплообмена. И поверочные (проверочные) – для определения количества переданного тепла и температур теплоносителей, т. е. когда теплообменник уже существует.

Расчет любых теплообменников должен включать в себя и гидромеханический расчет, т. е. расчет энергии на движение теплоносителей через аппарат. Мощность на валу насоса или вентилятора

N = G∆p/ρη , Вт …( 57)

где G – массовый расход (кг/сек);

∆p – полное сопротивление трения по пути движения жидкости и местные сопротивления, мешающие её продвижению (н/м²);

ρ – плотность жидкости или газа ( кг/м³) ;

η – к. п. д. насоса или вентилятора .

При выборе форм и размеров поверхности нагрева не следует забывать о расходе энергии на движение теплоносителей. В этом плане целесообразен технико – экономический расчет.

Тепловой расчет регенеративных теплообменных аппаратов

Решения сводятся в дополнении и решении уравнений, приведенных выше, уравнениями процесса теплопроводности для термически ‘’тонких’’ тел, что представлено выше и, например , в описании лабораторной работы №4. Появляются понятия необходимого времени нагрева (охлаждения) и охлаждения (нагрева) служащих для этих целей т. наз. насадок. Подробно об этом говорится в специальной литературе.

ЛИТЕРАТУРА

1.Карслоу Г.С., Егер Д.К.. Теплопроводность твердых тел, М., 1964.

2. Лыков А.В. Теория теплопроводности, М., 1967.

3.Исаченко В.П, Осипова В.А., Сукомел А.С.. Теплопередача, М., Л., 1965.

4.Арюткин Ю.И. , Курякин В.Ф., Семенов Ю.К.

Расчетно-экспериментальный метод решения температурных задач при переменных по координате и во времени граничных условиях . Инженерно-физический журнал, Т.61, N3, 1991.

Экспериментально-теоретический метод определения температурных полей сложных конструкций. ИФЖ, Т.57, N4, 1989.

5. Арюткин Ю.И., Курякин В.Ф., Семенов Ю.К.

Решение прямых и обратных задач теплопроводности с использованием уравнений типа свертки. Вопросы атомной науки и техники. Методики и программы численного решения задач математической физики, Вып.3, 1985.

6. Новиков С.А., Семенов Ю.К., Желонкин В.Ф.

Сборник решений задач и лабораторных работ по курсу “Техническая термодинамика и теплопередача”, САРФТИ МИФИ , 1998.

7. Илькаев Р. И., Новиков С. А., Семенов Ю. К. и др.

ВЗРЫВЧАТЫЕ ВЕЩЕСТВА,Учебное пособие, Том Ι, Глава ΙẊ, РФЯЦ- ВНИИЭФ, Саров, 2001.

Страниц – 27 , формул – 57 ,таблиц -2 ,рисунков – 8 ,емкость ≈2 Мб .

Составил к. ф. –м. н. , с. н. с. , доцент п/п Ю. К. Семенов.