2.Нестационарные задачи теплопроводности твердых тел

Наиболее просты решения для термически “тонких” тел, в которых, когда , несмотря на их размеры, температура на любой координате практически одинакова и зависит только от времени ( тела из высокотеплопроводного материала, например металлические ) . Тогда уравнения (3),(6) упрощаются и с учетом граничных условий, например, третьего рода, сводятся к уравнению

Vρc(dt/dτ) = q = αF(t – t_ср) , т. е. …(22)

dt/dτ = m(t – t_ср), …(23)

где m = αF/(Vρc) – темп охлаждения (нагрева), час^-1 (α – коэффициент теплоотдачи ; F и V – наружная площадь и объем тела; ρ, с – плотность, удельная теплоемкость) , (Vρ – вес, кг ) , t₀ и t_ср - начальная температура объекта и температура внешней среды.

Решение (23) при t_ср = const и начальной температуре объекта t = t_нач = t₀

Θ = (t – t₀)/ (t_ср – t₀ ) =1 – е ^–mτ . …(24)

При линейном росте температуры среды t_ср = ( t₀ + Вτ) решение (23)

( t – t₀) = Bτ - (B/m)(1 – e ^–mτ ) ≈ Bτ – B/m …(25)

( B/m – отставание , тепловая инерция ,⁰ С).

При гармоническом законе изменения температуры среды, например, суточных колебаниях t_c = t_cp + Acosωτ ( A – амлитуда , ω = 2π/T =2π/24 = 0,262 рад/час = 57,3⁰/час – частота колебаний) приближенное решение уравнения (23)

( t – t_ср) ≈ Bcos(ωτ – β) , …(26)

где В = Аcosβ , а β = arctg(ω/m).

Т. е. амплитуда колебаний температуры объекта в cosβ раз меньше амплитуды колебаний температуры среды А , и отстает от нее по фазе на β (может быть и другого знака относительно температуры среды ). Более точные решения для этого случая привести нет возможности.

Вышеприведенные соотношения пригодны для оценки температур обычных тел, в которых температура зависит и от времени и от координат.

При симметричном нагреве (охлаждении) неограниченной пластины толщиной 2R, сплошного неограниченного цилиндра, сплошной сферы радиуса R от постоянной начальной температуры t_нач. температура является функцией только координаты r и времени , t = t(r, ). Граничные условия в этом случае в центре упрощаются: q = - 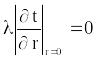; если постоянные во времени граничные условия на поверхности  рода: t_R=t_ср.= const;  рода - q = 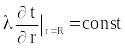,  рода - . Более сложные граничные условия здесь не рассматриваются.

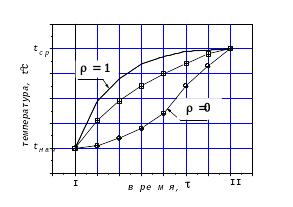
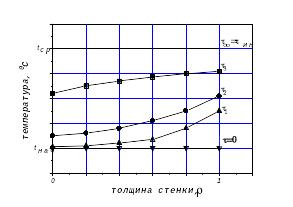
Применяют два способа графического представления решений: для фиксированных координат (и среднеинтегральной температуры) строят график зависимости их температур во времени t-, или для фиксированных значений времени изображают распределения температур по координате t-, т.наз. мультипликативную картину (рис.2).

время, Безразмерная координата  

_{1 } ₂  ₃......

Рис.2 Распределение температур при нестационарном нагреве.

При граничных условиях  рода тело из стационарного теплового состояния с начальной температурой t_нач. переходит в новое стационарное состояние с температурой среды t _ср за время тепловой инерции _ин. .Теоретически это время стремится к бесконечности, поэтому оперируют (5-10) % недонагревом (недоохлаждением) от начального температурного перепада (t_ср.-t_нач.), или отклонением от температуры среды в пределах точности измерения температур  2С. Следует отметить, что значения среднеинтегральных избыточных температур ( относительно температур границ) и термонапряжений (формула 18) имеют экстремум в начальный период процесса (при _ин..  24 часа примерно через 3-5 часов), в стационарном тепловом состоянии они равны нулю. Подробнее это исследуется при выполнении лабораторной работы № 3 [6].

Aналитическое решение задач целесообразно выразить через безразмерные параметры:

- безразмерная координата

- безразмерная температура , .

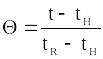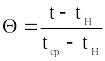при граничных условиях   рода соответственно, [0...1] и 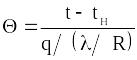при граничных условиях  рода, [0... ] ;

- безразмерное время F₀ = - критерий Фурье, [0... ] ;

- критерий Био Bi = , характеризующий отношение интенсивности внешнего теплообмена к внутреннему при граничных условиях  рода.

В безразмерной форме дифференциальное уравнение теплопроводности (6) принимает вид

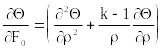…(27)

,

а граничные условия  рода: ; I  рода:

;  рода: .

После получения аналитического решения задачи в безразмерной форме переход к размерным температурам , координатам и времени производится в обратной последовательности t = t_нач. + (t_R -t_нач.), t = t_нач.+ (t_cp -t_нач.), t = t_нач.+ q/ при граничных условиях  рода соответственно; r = . Это позволяет, получив один раз решение для пластины, цилиндра или шара в безразмерной форме, рассматривать различные сочетания начальных температур и температур среды, тепловых потоков, линейных размеров, теплофизических характеристик материала и т.п. ( в том числе без разницы идет нагрев или охлаждение в диапазоне положительных и/или отрицательных температур ).

Диапазон величин Bi и F₀ , с которым можно встречаться на практике, огромен. При значении 0,02 м²/час (плохой проводник тепла - песчанная почва) для тонкого слоя толщиной 1 см критерий Фурье становится большим уже через минуту, F₀ = и нагрев (охлаждение) практически заканчивается; тогда как для тела с размером Земли F₀ остается малым в течение целых геологических эпох [2].

Опробованы различные аналитические решения Карслоу и Лыкова [1,2] . Анализ результатов показал, что отдельные из них нуждаются в доработке для малых значений критерия Фурье, что и было сделано. Все решения представляются для безразмерных температур и среднеинтегральных температур единообразно в форме

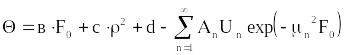, …(28)

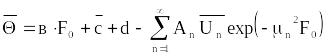, … (29)

n = 1,2... .

В таблице 2 сведены выражения для в,с, ,d,A_n,U_n, и уравнения для нахождения корней .

Решения при предельном числе членов ряда n = 100 с достаточной для практики точностью удовлетворяют значениям F₀  0,2 10^-3 (погрешность не более 0,01 %). При необходимости расчета для меньших значений F₀ достаточно увеличить число членов ряда.^*)

При значениях F₀>1/4 наступает, так называемый “регулярный“ (упорядоченный) тепловой режим, когда в случае граничных условий , рода можно ограничиться первым членом сумм рядов (процесс нагрева или охлаждения идет по экспоненте), а в случае граничных условий  рода вообще не учитывать и первый член суммы (процесс идет уже линейно во времени =вF₀ , а профиль температур по координате - квадратичная порабола с² вне зависимости от формы тела. Что касается среднеинтегральной температуры при граничных условиях ɪɪ рода, то она с самого начала описывается просто без составляющих суммы ряда.