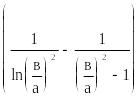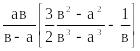1.Стационарные задачи теплопроводности твердых тел

В условиях однозначности не требуется знать начальное распределение температуры.

Решение уравнения (7) для неограниченной пластины, неограниченного полого цилиндра, полого шара соответственно

t=A+Br , … (8)

t=C+D ln r, … (9)

t=E- , … (10)

где

A,B,C,D,E,F - постоянные, определяемые из граничных условий слева r=а и справа r=в пластины внутри и снаружи полого цилиндра, полого шара. Из (8-10) видно, что температура в пластине изменяется линейно, в цилиндре - по логарифму, а в шаре - по гиперболе (наиболее резко) вне зависимости от граничных условий.

Рис. 1. Распределение температуры в стационарном состоянии.

t_a = t(r = a), t_b = t(r = b), t = t(r).

Удельный тепловой поток на координате r q = - r для пластины, цилиндра, шара

q = - , … (11)

q = - D/r , … (12)

q = - F/r² … (13)

соответственно. В пластине тепловой поток не зависит от координаты, в цилиндре и шаре убывает с ростом координаты, т.к. растет площадь поверхности.

Важным параметром теплового состояния тела является его средняя температура, точнее среднеинтегральная температура = (V - объем тела). Для пластины, цилиндра, шара

= ^(k-1)dr. … (14)

Пластина: = A + B ; … (15)

цилиндр: = C + D(ln в+ ) ; … (16)

шар: = E - F . … (17)

Представляет интерес координата с температурой, равной среднеинтегральной, она находится приравниванием выражений для t(r) и . На этой координате, например, в цилиндре и шаре отсутствуют тангенциальные температурные напряжения, на границах они максимальны (и разного знака)

_а,в = ( - t_а,в), …(18)

где

- коэффициент линейного расширения, модуль упругости, коэффициент Пуассона материала;

( - t_а,в) - среднеинтегральная избыточная температура относительно границ r = а или r = в соответственно.

Для пластины = , …(19)

т.е. находится в середине.

Для цилиндра = exp[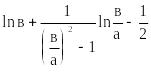 ] , …(20)

для шара = , … (21)

и они смещены от середины к наружной поверхности. От граничных условий месторасположение координаты в стационарных условиях не зависит

С целью обобщения результатов используется безразмерная температура = (t_r - t_в)/(t_а – t_в) и безразмерная среднеинтегральная температура = 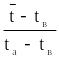- избыточные температуры относительно наружной поверхности, отнесенные к разности температур внутренней и наружной поверхностей.

Переход к размерным температурам производится обычным образом

t = t_в + , , . В безразмерных температурах и выражениях для удельных тепловых потоков на границах r=a, r=в нет постоянных А,В, или С,Д, или E,F, но для перехода к размерным температурам надо знать температуры поверхностей, а для вычисления тепловых потоков надо знать температурный перепад и коэффициент теплопроводности .

В таблице 1 представлены расчетные соотношения для вычисления в пластине, k = 1; полом цилиндре, k = 2; полом шаре ,k = 3.

Для расчета температурного поля, тепловых потоков, среднеинтегральных температур, координат с температурой равной среднеинтегральной в пластине, цилиндрической и сферической стенках при граничных условиях  есть программа HEAT1 для персонального компьютера на Фортране [6].

Таблица 1. Расчетные соотношения стационарной задачи теплопроводности.

K
1
2						exp
3

При задании на одной из поверхностей граничных условий  рода, т.е. q_a или q_в по соотношениям таблицы 1 можно найти t=(t_a-t_в) , но для определения поля температур надо еще знать и температуру в одной точке, например, t_в , иначе задача становится неопределенной. При граничных условиях  рода, т.е. задании температуры среды t_ср. и коэффициента теплоотдачи для нахождения температуры поверхности надо знать тепловой поток q_a или q_в (или ), либо температуру среды и коэффициент теплоотдачи на другой поверхности. Подробно эти задачи рассмотрены в [3].