Табличный метод анализа связи. Корреляционное отношение
Использование аналитической группировки в изучении корреляционной связи включает следующие этапы:
1) теоретическое обоснование модели регрессии;
2) оценка линии регрессии;
3) измерение тесноты связи;
4) проверка существенности связи.
В процессе выполнения первого этапа должны быть решены две задачи: теоретическое обоснование возможности наличия связи между изучаемыми признаками, выбор факторных признаков; определение числа групп и границ интервалов.
Оценка линии регрессии на втором этапе исследования заключается в расчете средних значениях результативного признака в выделенных группах.
На
третьем этапе
осуществляется измерение тесноты
связи, то есть определение роли изучаемого
фактора в формировании уровня значений
результативного признака. В качестве
показателя тесноты связи применяется
корреляционное отношение (
).
Этот показатель характеризует удельный
вес вариации, обусловленной группировочным
признаком, в общей дисперсии:
При
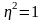каждому значению факторного признака
соответствует только одно значение
результативного признака, то есть связь
между признаками является функциональной.
В случае отсутствия функциональной связи, как правило, корреляционное отношение не равно 0.
Для проверки неслучайного характера выявленных закономерностей проводится четвертый этап исследования – проверка существенности связи. Проверка существенности связи осуществляется путем сравнения фактического значения корреляционного отношения с критическим значением. Критическое значение - это такое максимально возможное значение корреляционного отношения, которое может возникнуть при отсутствии связи между изучаемыми признаками.
Для проверки существенности связи помимо корреляционного отношения могут использоваться и другие критерии. Один из них – дисперсионное отношение F (критерий Фишера). Он рассчитывается следующим образом:
Критические значения критерия Фишера табулированы, они приведены в Приложении Б. Применение этих таблиц и порядок проверки существенности связи идентичны методам, описанным для корреляционного отношения.
Индексы. Общие и индивид.. Цепные и базисные. Сопряженные индексы
Индекс –
это относительный показатель, который выражает соотношение величин какого-либо явления во времени и пространстве или сравнение фактических данных с любым эталоном (план, прогноз, норматив и т.д.)
Индекс показывает во сколько раз уровень изучаемого явления в данных условиях отличается от аналогичного уровня в других условиях. Различие условий проявляется во времени, в пространстве, в выборе базы сравнения. Индексы выполняют аналитическую функцию – на их основе анализируется влияние факторов, определяющих динамику итоговых величин.
Классификация индексов:
По степени охвата явления:
индивидуальные;
сводные (общие).
По базе сравнения:
динамические;
территориальные.
По виду соизмерителей:
с постоянными весами;
с переменными весами